Закон всесвітнього тяжіння.  Прискорення вільного падіння.

Мета: сформувати знання про силу тяжіння та силу всесвітнього тяжіння (закон тяжіння).

Очікувані результати: учні повинні формулювати та записувати закон всесвітнього тяжіння, називати межі його застосування; знати, яким є фізичний зміст гравітаційної сталої та чому вона дорівнює; давати означення сили тяжіння, розуміти, як вона напрямлена та за якими формулами її обчислюють; знати, як розрахувати прискорення вільного падіння, від яких чинників воно залежить.          Тип уроку. Комбінований.

Прилади та матеріали для роботи з учнями:

•        Флеш – анімація Ньютонова гармата

•        Флеш – анімація Перша та друга космічна швидкість  Флеш – анімація Вивід космічного корабля на орбіту

•        Флеш – анімація Орбітальні переходи

•        Флеш – анімація Штучні супутники землі

•        Флеш – анімація Ракета

•        Флеш – анімація Задачі на закон всесвітнього тяжіння

•        Флеш – анімація Падіння тіл

•        Падіння тіла в розрідженому просторі (трубка Ньютона)

•        Веб-документ. “Прискорення вільного падіння для деяких міст України”.

План

1.     Актуалізація опорних знань.

2.     Вивчення нового матеріалу. 

3.     Вчимося розв’язувати задачі.

4.     Запитання на закріплення вивченого. 

5.     Домашнє завдання.

Хід уроку

1.     Актуалізація опорних знань. Перевірка домашнього завдання.

2.     Вивчення нового матеріалу. 

1. Гравітаційна взаємодія

   Усі фізичні тіла у Всесвіті притягуються одне до одного - це явище називають всесвітнім тяжінням або гравітацією (від латин. gravitas — вага).

   Гравітаційна взаємодія - взаємодія, яка є властивою всім тілам у Всесвіті й виявляється в їхньому взаємному притяганні одне до одного.

    Гравітаційна взаємодія здійснюється завдяки особливому виду матерії - гравітаційному полю, яке існує навколо будь-якого тіла.

2. Закон всесвітнього тяжіння.

   Перші вислови про тяжіння зустрічаються в античних авторів. Давньогрецький мислитель Плутарх (бл. 46 - бл. 127 рр.) писав: «Місяць упав би на Землю як камінь, щойно зникла б сила його польоту» 

   У XVI-XVII ст. учені Європи повернулися до теорії існування взаємного притягання тіл.

Поштовхом до її відродження стали насамперед відкриття в астрономії: Миколай Коперник довів, що в центрі Сонячної системи розташоване Сонце, а всі планети обертаються навколо нього. Йоган Кеплер (1571-1630) відкрив закони руху планет навколо Сонця, Галілео Галілей створив телескоп і за його допомогою побачив супутники Юпітера.    Але чому планети обертаються навколо Сонця, яка сила втримує космічні тіла на орбітах? Одним із перших, хто це зрозумів, був англійський учений Роберт Гук (1635–1703).     Він висловив припущення про те, що сила притягання двох тіл прямо пропорційна масам цих тіл і обернено пропорційна квадрату відстані між ними.

Однак довести це йому не вдалося.

     Це зробив І. Ньютон, який і сформулював закон всесвітнього тяжіння: Гравітаційне притягання існує між усіма тілами; будь-які два тіла, розмірами яких можна знехтувати, притягуються одне до одного з силою, що прямо пропорційна масам цих тіл і обернено пропорційна квадрату відстані між ними:

F - сила всесвітнього тяжіння, Н; m₁ i m₂  - маси взаємодіючих тіл, кг; r –  відстань між матеріальними точками (центрами куль), м; G – гравітаційна стала (коефіцієнт пропорційності), Н^.м²/кг²    Гравітаційна стала чисельно дорівнює силі, з якою притягуються два тіла масою по 1 кг кожне, що знаходяться на відстані 1 м одне від одного.

                                                              ¹¹ H  м2

G                         6,6710  ₂         кг

Гравітаційна стала не залежить від середовища, в якому перебувають тіла, від їхнього руху, фізичних та хімічних властивостей. Її числове значення вперше визначив дослідним шляхом у 1798 році англійський вчений Г. Кавендіш.

3. Межі застосування закону всесвітнього тяжіння

Формула   дає точний результат у таких випадках:

1)                якщо розміри тіл нехтовно малі порівняно з відстанню між ними (тіла можна вважати матеріальними точками);

2)                якщо обидва тіла мають кулясту форму та сферичний розподіл речовини; 3) якщо одне з тіл - куля, розміри та маса якої значно більші, ніж розміри та маса другого тіла, яке перебуває на поверхні цієї кулі або на відстані від неї.

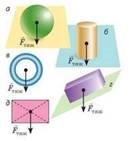
  Сила тяжіння напрямлена вертикально вниз і прикладена до точки, яку називають центром тяжіння тіла. Центр тяжіння однорідного симетричного тіла розташований у центрі симетрії; може бути й поза тілом.

4. Сила тяжіння

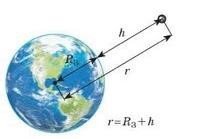
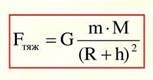
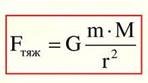   Сила тяжіння - сила, з якою Земля (або інше астрономічне тіло) притягує до себе тіла, що перебувають на її поверхні або поблизу неї.

 або

5. Прискорення вільного падіння

  Рух тіла лише під дією сили тяжіння називають вільним падінням.

   Під час вільного падіння сила тяжіння, що діє на тіло, жодною силою не скомпенсована, тому відповідно до другого закону Ньютона тіло рухається з прискоренням. Це прискорення називають прискоренням вільного падіння і позначають символом g.

З висотою над поверхнею Землі прискорення вільного падіння змінюється.

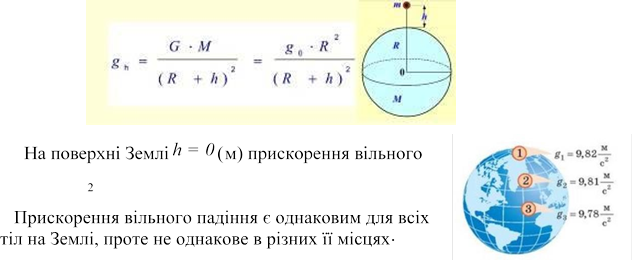падіння дорівнює  g ≈ 9,8 м/с .

3. Вчимося розв’язувати задачі.

Задача 1. Визначити значення сили взаємного притягання двох кораблів, віддалених один від одного на 100 м, якщо маса кожного з них 10 000 т.

 Розв’язання:

                                                   F₁                  F₂                                                                                     r  

F₁ = F₂ = F

                                                                                                   𝑚1𝑚2              𝑚2

                                                                                  𝐹 = 𝐺 𝑟₂ = 𝐺 𝑟2

                                                                                  𝐹  7Н              

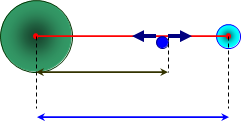
Задача 2.Середня відстань між центрами Землі і Місяця дорівнює 60 R (де R- радіус Землі). Маса Місяця у 81 раз менше маси Землі. В якій точці прямої, що з’єднує їх центри, тіло буде притягуватись до Землі і до Місяця з однаковими силами?

Розв’язання:

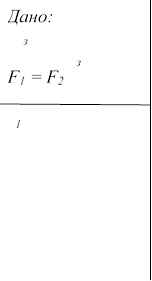М = 81 m                                          З                                                            

R = 60 R                                                               F₁  m₁  F₂     М

                                        r₁

r - ?                                                                                                                 r₂  

Позначимо масу тіла m₁, а його відстань від Землі r₁. 

Земля притягує дане тіло з силою:

                                                    F₁ = G M_зm₁/r₁² ,  а Місяць з силою:

                                F₂ = Gmm₁/(r – r₁)².  

   За умовою,  F₁ = F₂,   тоді  GM_зm₁/r²=Gmm₁/(r – r₁)²; 

                                              M_з(r – r₁)² = mr₁ . 

Оскільки M_з = 81 m ,  то 81 m (r – r₁)² = mr₁²;

                                     81(r² – 2rr₁ + r₁²) = r₁²;

                                    81 r² – 162 rr₁ + 81 r₁² - r₁² = 0.

 Маємо квадратне рівняння відносно r₁:

                                       80 r ₁² – 162 rr₁ + 81 r² = 0

Дискримінант D = (162 r)² – 4* 80*81 r² = 324 r²

Перший корінь рівняння   r₁ = 1,1 r – не задовольняє умову задачі; Другий корінь рівняння   r₂ = 0,85 r.

Отже,   r = 0,85 * 60 R_з = 51 R_з

Відповідь: Дане тіло знаходиться на відстані 51 R_з від центру Землі.

4. Запитання на закріплення вивченого. 

1.   Яку взаємодію називають гравітаційною? Наведіть приклади. 

2.   Запишіть закон всесвітнього тяжіння. 

3.   Яким є фізичний зміст гравітаційної сталої? Чому вона дорівнює? 

4.   Якими є межі застосування закону всесвітнього тяжіння?

5.   Дайте означення сили тяжіння. За якими формулами її обчислюють і як вона напрямлена?

6.   Від яких чинників залежить прискорення вільного падіння?

5. Домашнє завдання.

Вивчити параграф 33; виконати: вправа 33 (1, 2).