Формування предметної математичної компетентності в учнів через різні канали сприйняття інформації

Про матеріал

У змісті видання представлено питання формування предметної математичної компетентності в учнів через різні канали сприйняття інформації. Методичні рекомендації адресовані для вчителів закладів загальної середньої освіти.

Перегляд файлу

Відділ освіти

Білоцерківської районної державної адміністрації

Київської області

Інформаційно-методичний центр

Формування предметної математичної компетентності

в учнів через різні канали

сприйняття інформації

Методичні рекомендації

Біла Церква

2018

Формування предметної математичної компетентності в учнів через різні канали сприйняття інформації: методичні рекомендації/ уклад. М.А.Кумайгородська – Біла Церква: ІМЦ, 2018. – 56 с.

Розглянуто і схвалено на засіданні науково-методичної ради інформаційно-методичного центру відділу освіти Білоцерківської районної державної адміністрації.

Рецензент: Кравченко Н. Д. методист інформаційно-методичного центру відділу освіти Білоцерківської районної державної адміністрації, вчитель-методист

У змісті видання представлено питання формування предметної математичної компетентності в учнів через різні канали сприйняття інформації.

Методичні рекомендації адресовані для вчителів закладів загальної середньої освіти.

Зміст

І. ВСТУП . . . . . . . . . . . . . . . . . . . . . . . 4

ІІ. ОСНОВНА ЧАСТИНА . . . . . . . . . . . . . . . . 5

2.1. Компетентнісний підхід у навчанні. . . . . . . . . . . .5

2.2. Канали сприйняття інформації і їх співвідношення з педагогічною діяльністю. . . . . . . . . . . . . . . . . . 8

2.3. Формування предметної математичної компетентності в

учнів з різними каналами сприйняття інформації . . . . . 14

ІІІ. ВИСНОВКИ. . . . . . . . . . . . . . . . . . . . 17

ДОДАТКИ

Уроки в 5 класі з теми «Звичайні дроби». . . . . . . . . . . 18

Урок №1. Звичайні дроби. . . . . . . . . . . . . . . . . . 18

Урок №2. Звичайні дроби і ділення натуральних чисел. . . . .22

Урок №3. Розв'язування задач на дроби.. . . . . . . . . . .25

Урок №4. Порівняння звичайних дробів з однаковими

знаменниками. . . . . . . . . . . . . . . . . 28

Урок №5. Правильні і неправильні дроби.. . . . . . . . . 31

Урок №6. Мішані числа. .. . . . . . . . . . . . . . . . 34

Урок №7. Додавання та віднімання звичайних дробів з

однаковими знаменниками . . . . . . . . . . . .37

Урок №8. Додавання та віднімання звичайних дробів з

однаковими знаменниками. Розв’язування вправ . . . 41

Урок №9. Звичайні дроби. Урок систематизації та

узагальнення знань. . . . . . . . . . . . . . . . 44

Урок №10. Контрольна робота з теми «Звичайні дроби». . . . . 48

Методика «Тип пам’яті». . . . . . . . . . . . . . . . . 50

Методика «Образна пам'ять». . . . . . . . . . . . . . . 51

Методика «Спостереження особливостей сприймання». . . . 53

Використані джерела. . . . . . . . . . . . . . . . . . . 55

Для нотаток. . . . . . . . . . . . . . . . . . . . . . . 56

І. ВСТУП

«Мало мати хороший розум,

головне – гарно його застосовувати»

Р. Декарт

У Законі України «Про освіту» зазначено, що метою освіти є всебічний розвиток людини як особистості та найвищої цінності суспільства, її талантів, інтелектуальних, творчих і фізичних здібностей, формування цінностей і необхідних для успішної самореалізації компетентностей, виховання відповідальних громадян, які здатні до свідомого суспільного вибору та спрямування своєї діяльності на користь іншим людям і суспільству, збагачення на цій основі інтелектуального, економічного, творчого, культурного потенціалу Українського народу, підвищення освітнього рівня громадян задля забезпечення сталого розвитку України та її європейського вибору.

Концепція розвитку нової української школи стверджує необхідність якісного оновлення змісту освіти, забезпечення безперервного процесу становлення та розвитку гармонійної творчої особистості учня. Школа бере на себе місію створення нового освітнього середовища, де панує атмосфера педагогічної творчості вчителів-однодумців, учнів і батьків.

Нове освітнє середовище передбачає й новий зміст освіти, нові технології навчання і виховання, розвиток інтелектуальних здібностей дітей, щоб вивести кожного школяра на виховання культури творчого мислення. Все це вимагає інновацій у навчанні.

Інноваційне навчання спрямоване на розвиток учня, на формування його готовності до реального життя, швидких змін, творчого мислення, критичного аналізу навколишнього світу й усвідомленням себе в ньому, до постійного оволодіння учнями новими видами діяльності і спілкування.

Сучасний учень є партнером вчителя на уроці, а навчання – співробітництвом учителя й учня.

Для вчителя є важливим формування в учнів математичної компетентності як ключової, а також інших ключових компетентностей, зокрема комутативної, інформаційної, загальнонавчальної.

Враховуючи психологічні особливості учнів треба розпочинати роботу з дітьми у 5 класі налагоджуючи тісний взаємозв’язок через різні канали сприйняття інформації.

Процес психічного розвитку школяра має ґрунтуватися на гармонійній відповідності між психофізіологічними можливостями дитини та вимогами соціуму, звільняти від примусовості, підтримувати розвиток пізнавально-дослідницьких навичок, сприяти інформаційному збагаченню мислення та почуттів учнів.

ІІ.ОСНОВНА ЧАСТИНА

2.1. Компетентнісний підхід у навчанні

В новій програмі з математики вказано що, метою базової загальної середньої освіти є розвиток та соціалізація особистості учнів, формування їхньої національної самосвідомості, загальної культури, світоглядних орієнтирів, екологічного стилю мислення і поведінки, творчих здібностей, дослідницьких навичок і навичок життєзабезпечення, здатності до саморозвитку та самонавчання в умовах глобальних змін і викликів. Провідним засобом реалізації вказаної мети є запровадження компетентнісного підходу у навчально-виховний процес загальноосвітньої школи шляхом формування предметних і ключових компетентностей.

Це означає, що одержуючи математичну підготовку, учні мають здобути не лише знання й уміння суто предметного характеру, але й досвід їх практичного застосування, значно розвинути природне математичне бачення та інтуїцію, набути первинних навичок і вмінь, несуперечливо і доказово міркувати, навчити обирати кращий шлях для розв’язання певної проблеми в умовах їх варіативності.

Передумови успішної освіти (за доповіддю Жака Делора «Освіта: прихований скарб»):

А це багато в чому залежить не від отриманих знань і вмінь, а від додаткових рис та вправності, на позначення яких і вживають поняття «компетенції» та «компетентності», що відповідають розумінню сучасних завдань освіти.

Компетенція – це коло питань, явищ, у яких людина компетентна, має відповідний рівень пізнання й досвід. Наприклад: освітня компетенція учнів, педагогічна компетенція вчителя, медична компетенція лікаря тощо.

Компетентний:

1) той, хто знає, обізнаний, авторитетний у певній галузі;

2) фахівець, що володіє компетентністю.

Компетентність – це здатність установити й реалізувати зв’язок між «знанням – умінням» і ситуацією.

Основні складові компетентності:

Знання, а не просто інформація, що швидко змінюється. Різновиди знань, які необхідно вміти знайти і спрямувати в русло своєї діяльності.
Уміння використовувати ці знання в конкретній ситуації, розуміння, яким способом можна здобути ці знання.
Адекватне оцінювання – себе, світу, свого місця у світі, конкретних знань, необхідності їх для своєї діяльності, а також методу їх отримання або використання.

Цю формулу логічно можна подати в такий спосіб: компетентність = мобільність знань + гнучкість методу + критичність мислення.

Компетентнісний підхід протистоїть:

традиційному предметному навчанню, в основі якого – ідея трансляції та засвоєння знань (інформації);
селективній, дворівневій (знає – не знає) системі оцінювання;
примусовим формам організації навчальних занять (як у конвеєрному способі організації праці);
вертикальній, ієрархічно організованій системі адміністративного керування.

Компетентність – це не специфічні предметні вміння та навички, навіть не абстрактні розумові дії або логічні операції, а конкретні, життєві, необхідні людині дії будь-якої професії та віку.

Рівень освіченості, особливо за сучасних умов, не визначається обсягом знань, їх енциклопедичністю. Із позицій компетентнісного підходу рівень освіченості визначається здатністю розв’язувати проблеми різної складності на основі наявних знань. Компетентнісний підхід не заперечує значення знань, але він акцентує увагу на здатності використовувати здобуті знання.

Принципи компетентнісного підходу в освіті:

Освіта для життя, успішної соціалізації в суспільстві та особистісного розвитку на основі засвоєння учнями соціально значущих умінь (компетенцій).
Оцінювання для надання можливості учневі самому планувати свої освітні результати й удосконалювати їх у процесі постійної самооцінки.
Різноманітні форми організації самостійної, осмисленої діяльності учнів на основі власної мотивації та відповідальності за результат.
Матрична система управління, делегування повноважень, залучення батьків, учнів і людей із зовнішнього оточення до управління освітою та оцінювання діяльності, свобода вчителя у виборі засобів прищеплення учням соціальних пріоритетів (компетенцій).

Що означає для освіти переорієнтація на компетентнісний підхід?

Слід відмовитися від так званої енциклопедичності змісту шкільного навчання і формувати в школярів передусім ті знання, які є необхідними для використання практичних, ситуативних, особистісно-орієнтованих комунікативних завдань.

Компетентнісний підхід тісно пов’язаний із такими вимогами до навчання, як

особистісно орієнтований (потребує трансформації змісту освіти, перетворення його з моделі «для всіх» на суб’єктивні надбання одного учня, що їх можна виміряти)
діяльнісний (може бути реалізований тільки в діяльності, тобто в процесі використання конкретним учнем певного комплексу дій).

Що дає формування компетентностей…?

Дитині – підтримку позитивної мотивації, розвиток інтересу; батькам – оптимальні умови навчання і розвитку дитини; вчителю – професійне зростання; школі – зміцнення позитивного іміджу; суспільству – підвищення якості шкільної освіти.

Перехід до компетентнісного підходу означає:

а) переорієнтацію з процесу на результат освіти в діяльнісному вимірі;

б) зміцнення акценту з накопичування нормативно визначених знань, умінь і навичок на формування й розвиток в учнів здатності практично діяти, застосовувати досвід успішних дій у конкретних ситуаціях.

Результати навчальної діяльності розглядають як особисті досягнення учнів.Важливим стає не наявність у нього внутрішньої організації знань, а здатність застосовувати компетентності в навчанні та житті.

Яка правова база запровадження компетентнісного підходу?

Про компетентнісний підхід до формування змісту освіти йдеться в Державних Стандартах освіти, його реалізовано в Критеріях навчальних досягнень.

Перелік ключових компетентностей, визначених наказом МОН №371

Вміння вчитися.
Здоров’язберігаюча.
Загальнокультурна.
Соціально-трудова.
Інформаційна (ІКТ).

Зміни у змісті освіти, а саме:

широке впровадження в практику навчання компетентнісного підходу;
компетентнісний урок;
зміни в методиці;
впровадження курсів за вибором, спецкурсів, факультативів.

Мета застосування компетентнісної технології.

Учні швидше засвоюють програмовий матеріал з різних предметів.
Спокійніше і впевненіше відповідають, виконують самостійні роботи, мають дослідницькі навички.
Уміють запропонувати свій спосіб діяльності, аргументувати свої думки.
Уміють відстоювати свою точку зору.
Краще володіють навичками самоконтролю й самооцінки.

2.2. Канали сприйняття інформації і їх співвідношення

з педагогічною діяльністю

Актуальною є проблема навчання дітей з різними каналами сприйняття інформації і їх співвідношення з педагогічною діяльністю. Щоб кожна дитина була почута і зрозуміла в процесі уроку, завдання учителя знайти гнучкий спосіб взаємодії з учнями. Це можливо здійснити, керуючись інформацією про канали сприйняття ними інформації.

Від правильного використання каналів сприйняття інформації залежить якість сприйнятої інформації, швидкість виникнення почуттів, їх тривалість і стійкість, кмітливість, спрямованість на визначені контакти з іншими предметами і людьми, на інтерес людини до себе та навколишнього світу.

Говорячи про канали сприйняття інформації, слід мати на увазі насамперед фізичні способи сприйняття і одержання інформації. Фізіологи і нейролінгвістичні програмісти ділять їх на візуальну, аудіальну та кінестетичну системи.

Усі люди запам’ятовують інформацію по-різному. Так, ті, хто отримуєінформацію через слуховий канал, називаються аудіалами. Візуал – целюдина, яка сприймає більшість інформації з допомогою зору. Кінестетик – той, хто сприймає інформацію через інші відчуття (дотик, нюх тощо). Є також люди, у яких сприйняття інформації відбувається через логічне осмислення, з допомогою цифр, знаків, логічних доказів, вони називаються дискрети або дигітали. Проте така категорія людей трапляється найрідше, а серед дітей чи навіть школярів – особливо рідко.

Учителі вшколі, як правило, орієнтовані на слуховий канал. Більшість інформації подається на слух. Тому дитина-візуал досить погано сприймає шкільну інформацію. Добре, якщо на уроках учителі задіюють усі канали сприймання. Канали сприйняття ґрунтуються на фізичних способах сприйняття і отримання нової інформації.

До загальновживаних каналів сприйняття відносять зоровий канал (зорово-сприймаючі особи), слуховий канал (слухо-сприймаючі особи) і моторний канал (моторно-сприймаючі особи).

Зоровий канал сприйняття – це когнітивна здатність сприймати нову інформацію переважно за допомоги зору. Якісні ознаки нової інформації, на які реагує носій цього стилю в процесі сприйняття і обробки інформації, це – яскравість, розмір і колір, його насиченість, сила і чистота; контрастність; фактура; форма і симетрія, а також вербальні та невербальні засоби, що визначають перераховані вище поняття.

Слуховий канал сприйняття – це когнітивна здатність сприйняття і обробки нової інформації, у першу чергу спираючись на слух. Якісні особливості, наякі реагують такі особи, це, перш за все, висота тону або звуку, темп, гучність, ритм, тембр і резонанс. Під час занять такі особи відрізняються своїм природним тяжінням до усного викладу матеріалу. Отже, фільми, будь-які форми аудіо-спілкування, аудіо-доповіді і аудіо-лекції виявляються особливо корисними в процесі навчання слухо-сприймаючих слухачів.

Моторний канал сприйняття (кінестетики). Моторно-сприймаючі слухачі при надбанні нової інформації спираються на рух і відчуття. Якості, якнайважливіші для них у взаємодії з новою інформацією, це – частота, тиск, тривалість дії, інтенсивність уваги, а також позитивні чи негативні реакції на діяльність.
Більшість людей володіє першим і другим з визначених каналів сприйняття. Дехто в процесі навчання користується навіть декількома стилями. І тільки зовсім невелика кількість людей, як з’ясувалося, не має переваг: всі канали сприйняття або навчання однаково підходять для них.

Аудіал. Людина що більш орієнтується на те, що він чує: музику, інтонації, тембр мови, на відміну від дигіталів, які більш орієнтовані на зміст мови. Людина, у якої первинна репрезентативна система аудіально-тональна.

Представники аудіальної групи мають гострий слух і чудову пам’ять. Вони прекрасні слухачі, що запам’ятовують подробиці розповіді.
Візуал. Людина, яка більш орієнтується на зір, ніж на відчуття і слух (у якої первинна репрезентативна система візуальна).Візуали також досить розповсюджена група — їх 30%. Візуал дивиться співрозмовнику в очі. Він упевнений, що його слухають тільки тоді, коли на нього дивляться.

Кінестетик. Людина, що більш орієнтується на власні відчуття і переживання, ніж на слух і зір, тобто з більш розвинутим кінестетичним каналом (у якого первинна репрезентативна система візуальна).Найбільш розповсюджений тип людини — кінестетики (40% населення). Під час спілкування вони можуть не дивитися на співрозмовника, але будуть постійно торкатися його рукою.

Дигітал. Людина, яка більш орієнтується на зміст і внутрішній діалог (у якої первинна репрезентативна система аудіально-дигітальна). У них сприйняття інформації відбувається восновному за допомогою логічного осмислення, за допомогою цифр, знаків, логічних доведень. Ця категорія мабуть найменш чисельна серед людей взагалі. А для учнів молодших та середніх класів такий тип сприйняття, зазвичай, не є характерним.

Чому так важливо знати? Яким чином учень сприймає інформацію?
Під час уроку вчитель може викладати матеріал використовуючи всі канали сприйняття: зір, слух та кінестетичний канал. Тоді у кожного учня є шанс засвоїти хоча б частину інформації. Зазвичай саме так і відбувається. Також шанси учня значно підвищуються якщо, наприклад, і вчитель і учень – візуали (чи аудіали). Кінестетиків, на жаль, серед педагогів взагалі небагато, а у середніх та старших класах їх взагалі немає (якщо не рахувати вчителів фізичної культури та праці). Від того, який канал у дитини є головним, залежить засвоєння багатьох важливих навичок. Наприклад, читання чи письмо.

У дітей з різним типом сприйняття суттєво відрізняються особливості розумової праці (наприклад, особливості запам’ятовування, рівень уваги тощо).

Якщо батьки співпрацюють з вчителем, спостерігають за поведінкою дитини та продіагностують її разом із вчителем, тоді їм легше будувати з нею відносини. Багато що стає зрозумілим: чому виникають проблеми з дисципліною, чому ми говоримо “різними мовами”, як саме правильно заохочувати дитину чи робити їй зауваження тощо.

Тепер коротко розглянемо ознаки, за якими ми можемо виявити головний канал сприйняття учня. На що обов’язково потрібно звернути увагу.

Словник спілкування

Візуал у своєму мовленні часто використовує слова, пов’язані із зором (дивитися, спостерігати, картина, на перший погляд, прозорий, яскравий, як бачите тощо). Для аудіала є характерним використання слів, пов’язаних із слуховим сприйняттям (голос, послухайте, обговорювати, мовчазний, тиша, голосний, мелодійний тощо). Словник кінестетиків в основному включає слова, що описують відчуття чи рух (схопити, м’який, теплий, дотик, пружний, добрий нюх тощо).

Напрям поглядів

У візуалів, під час спілкування, погляд в основному спрямований вгору, у аудіалів – по середній лінії, у кінестетиків – додолу.

Особливості уваги

Кінестетику взагалі важко концентрувати свою увагу, його може відволікти що завгодно; аудіала легко відволікають звуки; візуалу шум практично не заважає.

Особливості запам’ятовування

Візуал пам’ятає те, що бачив, запам’ятовує малюнки. Аудіал – те, що обговорював, слухав. Кінестетик пам’ятає загальне враження. Запам’ятовує рухи.

А скільки можливостей у вчителя та батьків поспостерігати за різними типами учнів у їх повсякденних справах! Наприклад, варто придивитися, хто як записує домашнє завдання. Припустимо, що воно записане на класній дошці.Візуал: слухняно відкриє щоденник і занотує, а вірніше перепише з дошки те, що задано на домашнє опрацювання. Він полюбляє володіти необхідною інформацією, ніж питати в інших. Він легко сприймає її записаною саме на дошці. Аудіал: якщо схоче записати домашнє завдання, то, швидше за все, перепитає у сусіда по парті, що задано. Прослухавши інформацію занотує її в щоденник. Вдома може “сидіти на телефоні” і дізнатися у однокласників, що задано. Або просить зробити це батьків і сказати йому. Кінестетик: найчастіше довго риється у своїй сумці, витягує звідти підручники, знаходить відповідні сторінки і просто у підручниках обводить номери необхідних вправ.

Багато чого може дати спостереження за поведінкою дітей під час перерви. Візуал: якщо більшість учнів покинуло класну кімнату, швидше за все залишиться у приміщенні. Для нього головне – це можливість спокійно зануритися у власні зорові образи. Та йому заважатимуть шумні балачки аудіалів чи рухливі ігри кінестетиків. Він може вийти до коридору, де буде спостерігати за іншими дітьми чи розглядати стенди.

Аудіали використовують перерву, щоб поговорити та погомоніти. Особливо, якщо на попередньому уроці довелося багато писати і мовчати.

Для кінестетика перерва потрібна, щоб розім’ятися, побігати.
Про що свідчать ці спостереження? Не варто змушувати всіх дітей на перерві грати у рухливі ігри або слухати тиху музику. Кожна дитина інстинктивно обирає той засіб відновлення сил, що допоможе саме їй. Так самоіндивідуально слід приділяти увагу до кожного з них під час навчального процесу.

Спеціалісти говорять:

• у візуала можна вимагати швидкого вирішення задач;
• від аудіала – чіткого повторення почутого ним матеріалу;

• від кінестетика краще не чекати ні того, ні іншого – він потребує особливого відношення, йому потрібно більше часу на вирішення певного завдання. У даному випадку є доцільним використовувати завдання на картках.

Під час виконання завдань на уроці чи вдома рекомендується:

• візуалу необхідно дозволити тримати біля себе аркуш паперу, на якому він підчас осмислення та запам’ятовування матеріалу може креслити малювати тощо;

• не треба робити зауваження аудіалу, коли він в процесі запам’ятовування тихенько говорить чи рухає губами – йому так легше запам’ятовувати матеріал та виконувати завдання;

• кінестетика не можна змушувати довго сидіти не рухаючись; обов’язково необхідно надавати йому можливість моторної розрядки (сходити за крейдою, писати на дошці, демонструвати муляж); запам’ятовування матеріалу у нього краще відбувається під час руху.

Зрозуміло, що дуже важливим є спілкування з дитиною “її мовою”:

• спілкуючись з візуалом використовуйте слова, що описують колір, розмір, форму, місцеположнення; на дошці підкреслюйте ізнокольоровою крейдою різні пункти чи аспекти змісту; використовуйте схеми, таблиці, наочні посібники тощо;

• пояснюючи матеріал аудіалу використовуйте вібрації голосу (інтонації, паузи, висота), відображаючи тілом ритм мовлення (особливо головою) зі швидкістю, характерною для цього типу сприйняття;

• для кінестетика є дуже важливим жести, дотики та типова для них повільна швидкість розумових процесів; пам’ятайте, що кінестетик навчається за допомогою м’язової пам’яті; чим більше перебільшення, тим краще для запам’ятовування; дозволяйте їм програти у різних ролях частини поданої інформації (наприклад, урок-вистава).

Навіть зауваження матиме кращий ефект, якщо буде зроблено “його мовою”:

• візуалу краще погрозити пальцем, похитати головою чи зробити “суворі очі”;

• аудіалу – сказати пошепки “ш-ш-ш”;

• кінестетику – покласти руку на плече, поплескати по ньому. Зрозуміло, що будь-яка людина протягом свого життя використовує різні канали сприйняття. Вона може бути за своєю природою візуалом, та це не значить, що інші органи чуттів у неї практично не працюють. Їх можна і потрібно розвивати. Чим більше каналів відкрито для прийняття інформації, тим ефективніше відбувається процес сприйняття.

2.3. Формування предметної математичної компетентності в учнів через різні канали сприйняття інформації

Щоб розвивати творчі здібності учнів починаючи з 5 класу, потрібно замислюватись насамперед над тим, як спланувати і організувати роботу дітей, щоб вони успішно засвоювали нові знання в міру закладених природних особливостей, не відчували дискомфорту при переході в старшу школу.

Викладання, як процес передбачає вибір найбільш вдалої (з огляду на мету і завдання) структури уроку, тобто послідовності опитування, вивчення нового, закріплення, узагальнення і систематизації. Як показує практика, найбільшу частку навчального процесу займають уроки, в яких обов’язково присутній етап вивчення нового матеріалу.

В першу чергу, готуючи урок, вчитель задумується над мотивацією навчання, бо учні дуже часто задають запитання, яку оцінку отримують, чим будуть винагородженні за виконання завдань. Спостереження за розвитком рівня знань кожного учня роблять можливим підхід до створення ситуації, в якій відбувається мотивування учня щодо самовдосконалення та самоорганізації. Допомогу вчителю додадуть знання психологічних особливостей, тобто знання про те, якими каналами учень краще сприймає інформацію. Провівши тестування учнів щодо виявлення провідного каналу сприйняття інформації можна підібрати методи, форми роботи на уроці.

Індивідуальні відмінності різних каналів сприйняття інформації проявляються в пізнавальні сфері. На власному досвіді можна переконатися у тому, на скільки простіше вчити учнів, коли є взаєморозуміння (це коли вчитель і учень спілкуються на одному і тому ж каналі сприйняття інформації).

Застосування інноваційних методів саме і допоможе провести урок так, щоб всі учні отримали нові знання, уміння і навички в міру їх природних здібностей.

Найперше треба врахувати як правильно розсадити учнів за партами. Полюбляють сидіти ближче до вчителя старанні учні та такі, що мають певну мотивацію. Найважче для вивчення математика для кінестетиків, бо вони сприймають інформацію через емоційні почуття. На уроці їм важливий рух і вчитель має це враховувати:дозволити звірити розв’язання з товаришем, що сидить за іншою партою, та запланувати обов’язково для таких учнів вправи чи завдання на відтворення моделі навчального процесу власноруч. При вивченні математики в 5-6 класах я активно застосовую ПМК «Математика. 5 клас» та «Математика. 6 клас». Найчастіше вчитель розпочинає уроки із словесного оголошення теми та записом її на

дошці і в зошиті. Це легко сприймають аудіали і візуали. Наочність допомагає швидше засвоїти матеріал візуалам-іконістам. Важливо встановлювати зворотній зв'язок опираючись на аудіалів (аудіальних, що краще сприймають слухаючи інших). Зміна тембру голосу, надання чітких інструкцій в роботі допоможе співпрацювати з аудіалами. На уроці часто використовую допомогу аудіалів при складанні алгоритмів. Мовним аудіалам надаю можливість проговорити почуте. Якщо у класі більшість учнів кінестетиків то вивчати матеріал великими блоками недоречно – буде просто втрачений час. Візуалам легко засвоїти записи і читання. Тому у нагоді будуть схеми, таблиці, алгоритми.

Вивчення нового матеріалу психологи радять розподілять на декілька складових:

- входження учнів у простір нового матеріалу через усвідомлення понятійного апарату теми уроку;

- пояснення вчителя за допомогою дошки та кольорової крейди або дошки з сенсорним покриттям;

- використання схем, опорних конспектів,асоціативних зв’язків;

- робота учнів з текстом підручника або додатковими джерелами інформації;

- моделювання математичної ситуації навчального матеріалу;

- опанування матеріалу учнями через низку запитань і вправ;

- розробка алгоритму дій;

- робота учнів у зошитах з диференційованим підходом (запропонована основа для заповнення чи продовження записів, схем, рисунків тощо).

Продіагностувавши дітей 5 класу, вчитель має спостерігати за їх поведінкою на уроках і в позаурочний час, коригувати власну діяльність, намагатися розвивати у школярів дані природою канали сприйняття інформації, розширювати інтелектуальні здібності, розвивати творчі навички та підвищувати рівень знань.

ІІІ. ВИСНОВКИ

Навчання математики в 5 класі має зробити внесок у формування ключових компетентностей загальнонавчальної (уміння вчитися), комунікативної (грамотно формулювати і висловлювати судження), загально-культурної та інших. Формування зазначених компетентностей підпорядковується реалізації загальних завдань шкільної математичної освіти, кінцевим результатом якої є здатність учнів успішно діяти в навчальних і життєвих ситуаціях і нести відповідальність за свої дії

Важливо ураховувати індивідуальні психофізіологічні особливості дітей щоб вибрати на урок форми методи і засоби навчання. Вчитель, усвідомлюючи психолого-педагогічні проблеми, намагається викладати матеріал використовуючи всі канали сприйняття: зір, слух та кінестетичний канал. У кожного учня є шанс засвоїти хоча б частину інформації. Зазвичай саме так і відбувається. Також шанси учня значно підвищуються якщо, і вчитель і учень – візуали (чи аудіали). Від того, який канал у дитини є головним, залежить засвоєння багатьох важливих навичок.

Для учнів середньої школи доцільним є:

поєднання навчальної діяльності з ігровою;
поєднання різних форм роботи захищає більш слабкого учня від небажання вчитися, а також відчувати підтримку товаришів;
пояснення матеріалу на життєвих прикладах.

Рефлексія допомагає встановити рівень засвоєння матеріалу, формує свідомість, самосвідомість та зберігає психічне і соціальне здоров’я.

Чітка організація навчальної праці оберігає від втомлюваності учнів.

В цьому методичному виданні піднімається питання формування предметної математичної компетентності в учнів через різні канали сприйняття інформації. Підкреслюється важливість зазначеної проблеми і пропонуються практичні рекомендації необхідні вчителю під час роботи з учнями.

ДОДАТКИ

Уроки в 5 класі з теми «Звичайні дроби»

Урок №1

Тема. Звичайні дроби

Мета. Спираючись на отримані в молодших класах знання формувати поняття дробу, розкрити об’єктивну необхідність вивчення дробових чисел; розвивати логічне та креативне мислення;

виховувати цілеспрямованість, бажання працювати старанно, впевнено та творчо.

Тип уроку: формування нових знань та вмінь.

Формувати компетенції: наводити приклади звичайних дробів, пояснювати що означає чисельник та знаменник дробу; розв’язувати вправи, що передбачають знаходження дробу від числа і числа за його дробом.

Очікувані результати: розширення знань учнів про число; формування поняття звичайного дробу; забезпечення оволодіння математичною мовою.

Обладнання: набір моделей «Звичайні дроби», кольорова крейда, таблиця «Модель майбутніх знань», креслярське приладдя, підручник «Математика 5, Істер О.С., мультимедійний проектор, ноутбук, ПМК “Математика навчального призначення”, 5 клас, автори Білоус Наталія та інші.

Хід уроку

I. Мотивація навчальної діяльності

Вчитель: Друзі, прочитайте слова грецького філософа Аристотеля: «Будь-яке вчення і навчання ґрунтуються на раніше набутих знаннях». Як ви розумієте цей вислів?

II. Актуалізація опорних знань. Інтерактивна вправа «Мікрофон»

1.Чого більше: цифр чи чисел?

2.Скільки є цифр для запису чисел?

3.Яку систему числення ми використовуємо?

4.До якої множини входять числа, які ми вивчили в першому семестрі?

5.Які ще види чисел ви знаєте? Наведіть приклади.

6.В яких задачах виникає потреба використовувати звичайні дроби?

7.Як називають компоненти ділення? Чи завжди можливе ділення?

III. Мотивація (на малюнку або слайді)

Задача. В мами є два апельсини. Як їх розділити між трьома дітьми порівно?

Вч.:Чи отримують діти по цілому апельсину?

Для розв’язання задачі нам необхідно ввести нові числа, вміння їх читати і записувати.

За час зимових канікул учень дізнався більше про дробові числа. Послухаємо його повідомлення. Презентація «Історія виникнення звичайних дробів»(учень-аудіал або візуал).

IV. Вивчення нового матеріалу

Повідомлення теми. (Запис на дошці)

Методична вказівка: засвоєння матеріалу відбувається з врахуванням каналів сприйняття інформації: спочатку – аудіали (А), потім – візуали (В), і нарешті – кінестетики (К).

Вч. – Хтось може знає інші дроби?

Розглянемо «Модель майбутніх знань» (таблиця)

Обговорення інформації отриманої з моделі. (А).

Висновок: отже, раніше вивчені натуральні числа допоможуть утворювати звичайні дроби.

Дроби – це частинки, які виникають внаслідок ділення, якщо ділять одне ціле: предмет (яблуко, хлібину, торт) або одиницю виміру (метр, годину) на рівні частини, виникають дробові числа:

наприклад,

ПМК. Перегляд фрагменту№ 2 із уроку № 65 (для візуалів).

Демонстрація частин з набору моделей «Звичайні дроби». (В).

Вчитель пропонує кінестетику виконати практичні завдання:

на метровій лінійці,на циферблаті годинника;
ширина кімнати кабінету – 12 кроків. Зробити три кроки від початку кімнати, зупинитись і назвати, яку частину відстані він пройшов. Записує на дошці дріб .

Вчитель: Діти, зверніть увагу, що в записі цього дробу використано натуральні числа: 3; 12. Зробимо узагальнення: що таке звичайний дріб?

Читання правила з підручника. (А)

Запис вчителем на дошці, учнів – в зошиті:

Читання запису учнями (А), взаємоперевірка записів в зошитах по парах (В)

Вч. – напишіть по три приклади звичайних дробів, і прочитайте їх один одному.

Методична вказівка: за умови достатнього рівня математичної підготовки в класі після вивчення поняття дробу можна перейти до задач на дроби.

Задача 1. №919 (початковий рівень) або № 934 (середній рівень).

Задача 2. № 951 (достатній рівень).

Вчитель оформляє зразки записів задач.

V. Фізкультхвилинка

Ми писали, ми трудились,

наші руки вже стомились.

А щоб гарно написати,

треба пальці розім’яти.

Руки кілька раз тряхнемо

і писати знов почнемо.

VI. Первинне засвоєння нового матеріалу за підручником

Методична вказівка: номери завдань записані на дошці, щоб учні могли самостійно працювати, №№ 921, 923, 926, 929. Вчитель надає необхідну індивідуальну допомогу. За потребою, викликає учнів до дошки.

VII. Підсумок уроку

Що нового дізналися на уроці?
Чого навчилися?
Які знання здобули на уроці?

VIII. Оцінювання роботи учнів на уроці

IX. Домашнє завдання (диференційоване)

Опрацювати § 27, №№ 930, 945 або №№ 941, 952.

Урок №2

Тема.Звичайні дроби і ділення натуральних чисел

Мета. Подальше сприяння засвоєння учнями поняття звичайний дріб, формування вмінь читання і запису дробів та застосування їх до розв’язання задач, розвитку творчих здібностей, виховання наполегливості, математичної мови та культури записів.

Тип уроку: формування знань, застосування вмінь та навичок.

Обладнання: креслярське приладдя, кольорова крейда, підручник, модель майбутніх знань, ноутбук, ПМК “Математика навчального призначення”, 5 клас, автори Білоус Наталія та інші.

Хід уроку

Організаційний момент
II. Перевірка домашнього завдання «Знайди помилку»

Учні переглядають записи на дощці і відшукують помилки у розв’язаннях (учні-аудіали коментар; - візуали з кінестетиками можуть продемонструвати малюнок до задачі) .

№ 945

, , , , , , ,

№ 941

Маса дині – 3 кг 600 г – 1 ціла

Іван відрізав – ? кг – частину

Марія відрізала – ? кг – частину

Маса дині залишилась – ? кг

Розв’язання

1) 3 кг 600 г : 6 = 3000 г : 6 + 600 г : 6 = 500 г + 100 г = 600 г – відрізав Іван;

2) 3 кг 600 г : 9=3600 г : 9 = 400 г – відрізала Марія;

3) 3600 г – (600 г + 400 г) = 2600 г = 2 кг 600 г – залишилось.

Відповідь: 2 кг 600 г.

Мотивація: «Є одне благо – знання і одне зло – неуцтво». Сократ

III. Актуалізація опорних знань

Математичний диктант: незакінчені речення (аудіали на закритій дошці, візуали і кінестетики на картках).

Звичайний дріб записують за допомогою…
Де пишуть чисельник дробу…
Де пишуть знаменник дробу…
Знаменник означає…
Чисельник означає …
Щоб знайти дріб від числа треба …
Щоб знайти всю величину за дробом треба …
Одна десята частина тонни називається …
Одна дванадцята частина року називається …

10. Записати число 5 у вигляді дробу.

Методична вказівка: вчитель на власний розсуд перевіряє разом з учнями, або учні за допомогою взаємоперевірки зошитів.

Оголошення мети і завдання уроку.

Сьогодні ми розв’яжемо різні завдання на дроби і вдосконалимо знання запису та читання дробів

IV. Вивчення нового матеріалу

Скажіть будь ласка, дроби утворюються тільки під час ділення меншого натурального числа на більше?

ПМК. Перегляд фрагменту 3 із уроку№ 65 (В).

Відповідь: ні, у вигляді дробу записують ділення (частку) будь-яких натуральних чисел.

Наприклад: (малюнки чи слайди)

, , , , .

Хто помітив щось цікаве в цих записах?

, ,

Отже, будь-яке натуральне число можна подати у вигляді звичайного натурального дробу багатьма способами, змінюючи знаменник. В цій роботі вам допоможуть знання таблички множення і ділення.

V. Первинне закріплення

Виберіть будь-яке одноцифрове натуральне число і запишіть його кількома способами у вигляді звичайних дробів (підказку до завдання знайдіть в підручнику).

VI. Фізкультхвилинка

Працювати перестали. Покрутились, повертілись,

І тепер всі дружно встали. На хвилинку зупинились.

Будемо відпочивати, Пострибали, пострибали,

Нумо, вправу починати! Раз — присіли,

Руки вгору, руки вниз другий — встали.

І легесенько Всі за парти посідали.

VII. Розв’язування задач та вправ

№ 963, № 967 усні вправи (А)

№ 969, № 970, № 974 (письмові вправи переважно візуали або кінестетики)

Методична вказівка:письмові вправи виконуються біля дошки учнями за їх вибором.

VIII. Рефлексія

Чи задоволені ви своєю роботою на уроці?
Що для вас було складним?
Що для вас було найлегшим?
Як змінився ваш настрій на кінець уроку? (вчитель аналізує зміну настрою для планування наступного уроку.

IX. Домашне завдання (диференційоване)

Опрацювати §28; № 968, № 971, № 975

Урок №3

Тема. Розв'язування задач на дроби

Мета. Зміцнювати навички читання і запису звичайних дробів,формувати міцні навички розв’язування задач на дроби;розвивати пам'ять,увагу, вміння аналізувати задачу,записувати скорочену умову; виховувати активність, наполегливість у набутті знань,пропагувати математичний конкурс «Кенгуру».

Обладнання: кольорова крейда, дошка, підручник, мультимедійний

проектор, ноутбук, ПМК “Математика навчального

призначення”, 5 клас, автори Білоус Наталія та інші.

Епіграф: .«Якщо ви хочете навчитися плавати,то сміливо заходьте у воду, а якщо хочете навчитися розв’язувати задачі, то розв’язуйте їх» Д. Пойа

Хід уроку

I. Організаційний момент

Діти! Ми з вами часто розв’язуємо математичні задачі. Навчилися робити короткий запис до них. А сьогодні наше завдання на урок навчитися розв’язувати «задачі на дроби».

II. Мотивація навчальної діяльності учнів

Один із древніх мудреців сказав:« Хто не знає дробів, той не знає математики». Ви в мене наполегливі учні. Тому нам важливо набувати нових знань про дроби. Розпочнемо урок. Просигналізуйте смайликами який настрій у вас на початку уроку?



III. Актуалізація опорних знань

Фронтальне опитування.

Прочитайте дроби : (аудіали)

, , .

2. Яку частину фігури зображено: (візуали)

3. Яку частину від величини становить: (кінестети)

1коп = …грн.;1мм = …см;1хв = …год;1м = …км;1ц =… т;1с =…год

4. Яким числам відповідають точки на координатному промені? (візуали і кінестети)

IV. Пояснення теми

А) ПМК. Перегляд фрагменту 8 з уроку № 65.

( Вчитель пропонує кінестетам пояснити цю задачу на циферблаті годинника).

Б) Робота з підручником. Розбір розв’язаних задач №1, № 2 ст. 204 (читає аудіал; запис умови – візуал, відтворює кінестет за допомогою транспортира до задачі 1; на побудованому відрізку до задачі 2).

Задача 1. Задача 2.

Розгорнутий кут – 180⁰ Дорога АС – ? км

Частинка – ?⁰, Дорога АВ – 120 км, ч.

( відрізок АС 120 км

Розв'язання

1) 180⁰ : 5 · 2 = 72⁰ 1) 120 : 3 · 4 = 160 (км).

Відповідь: 72⁰ Відповідь: 160 км.

V. Фізкультхвилинка

Руки в сторони та вгору - Раз — присіли, руки прямо.

На носочки піднялись. Встали — знову все так само.

Підніми голівку вгору - Повертаємося вправно,

Й на долоньки подивись. Все виконуємо гарно.

Присідати ми почнемо, Вліво-вправо повернулись

Добре ноги розімнемо. І сусіду усміхнулись.

VI. Розв’язування задач за підручником №946, №953, №955 (вчитель викликає за бажанням до дошки учнів ).

VII. Розв’язування задач із збірника

Міжнародний математичний конкурс «Кенгуру 2014 -2015» ст.13

(№1, №6).

Задача №1

На якій із фігур, запропонованих у відповідях,зафарбована половина площі фігури?

Задача №6

Який із запропонованих у відповідях дробів менший, ніж 2?

А: Б: В: Г: Д:

VIII. Мотиваційне оцінювання учнів (заохочення до участі в конкурсі «Кенгуру»).

IX. Домашнє завдання: читати §29, (диференційоване) №947, №952 або №949, №956.

Урок №4

Тема. Порівняння звичайних дробів з однаковими знаменниками

Мета. Формувати вміння самостійно здобувати знання,

розвивати навички самооцінювання,

логічне та креативне мислення.

Обладнання:мультимедійний проектор, ноутбук,ПМК “Математика навчального призначення”, 5 клас, автори Білоус Наталія та інші

підручник, плакат «Телеграма Незнайки».

Хід уроку

I. Організаційний момент

Оголошення девізу уроку. І сувора й солов’їна

Математики країна.

Праця тут іде завзята.

Вмій лиш спритно працювати.

II. Актуалізація опорних знань

Діти, я щойно отримала телеграму. Незнайко просить допомоги: він не вміє розв’язати таке завдання.

Задача Незнайки

$D:\Пісні\музика для презентації\pictures\106019.tif$

Два яблука розділили між

трьома дівчатками, а чотири яблука

розділили між трьома хлопчиками.

Кому дісталася більша частинка

яблука?

Одній дівчинці: Одному хлопчику:

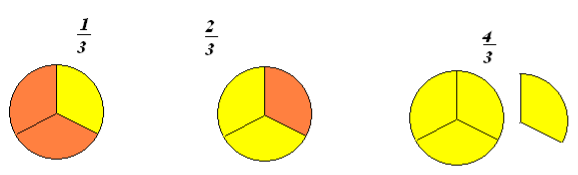
Діти, зверніть увагу! Ми щойно розв’язали дві математичні задачі, які часто трапляється в житті:

розділити на рівні частини;
порівняти різні частини

Проблемне завдання на урок:

опрацювати правило порівняння дробів з однаковими знаменниками.

Запис в зошити теми уроку: «Порівняння звичайних дробів з однаковими знаменниками».

III. Вивчення нового матеріалу

ПМК. Перегляд 2-3 фрагментів з уроку № 70 (для візуалів)

2 фрагмент: «Числовий промінь»,

3 фрагмент: «Порівняння дробів з однаковими знаменниками»,

Робота з підручником (с. 217, «Математика. 5 клас» О. Істер)

Читання правил порівняння дробів з однаковими знаменниками:

з використанням координатного променя. (для аудіалів та кінестетиків)

IV. Закріплення, виконання завдання

№ 984 (побудова дробів на координатному промені). Порівняння побудованих чисел.

(Будують візуали)

Порівняння з однаковими знаменниками (с. 216, «Математика. 5 клас» О.Істер). (Читають аудіали)

№ 979, № 980 (усно). (Коментують аудіали)

ПМК. Перегляд 6 фрагменту: «Порівняння дробів з однаковими чисельниками».

Робота з підручником (с. 219, «Математика. 5 клас» О. Істер). Обговорення малюнка 239. Використати стрічку з позначками половини і четвертої частин (демонструють кінестетики).

Закріплення, виконання завдання №996 (письмово).

V. Фізкультхвилинка

Трішки ми попрацювали, За щасливий день вчорашній,

Свою силу витрачали. І до сонця потягніться.

Треба нам би відпочити – В різні боки похиліться,

Свої сили відновити. Веретеном покрутіться,

Встаньте діти, посміхніться! Раз присядьте, два присядьте

Землі нашій поклоніться І за парти тихо сядьте.

VI. Розвиток пізнавальних інтересів та пізнавальної активності учнів через залучення їх до самостійного пошуку й «відкриття» нових знань, розв’язання задач проблемного характеру.

А). Виконання №991. Запис усіх натуральних значень а при яких дріб менший дробу .

Б). На координатному промені побудувати числа: .

Використовуючи побудову запиши задані числа в порядку зростання (спадання).

В). № 993. Знайти всі натуральні значення b, при яких дріб , більший за дріб але менший за дріб .

Г). Розв’яжіть рівняння:

VII. Рефлексія

Закінчити фразу:

Сьогодні на уроці …
Моя оцінка…

VIII. Підбиття підсумків уроку

Коментоване оцінювання учнів.

IX. Домашнє завдання: опрацювати §29, (диференційоване)

№982, №989, №994.

Урок №5

Тема. Правильні і неправильні дроби

Мета. Формувати поняття «правильний та неправильний дріб», розвивати навички зображення дробів на координатному промені,культуру математичного мовлення,порівняння дробів між собою. Виховувати позитивне ставлення до математики, культуру спілкування між учнями.

Обладнання: ноутбук, ПМК “Математика навчального призначення”, 5 клас, автори Білоус Наталія та інші, підручник, кольорова крейда.

Хід уроку

I. Організаційний момент

Взаємоперевірка домашнього завдання. Оцінювання.

II. Мотивація навчальної діяльності

Найдавнішою пам’яткою Київської Русі з арифметики є твір «Як людині пізнати числення літ», написаний слов’янською мовою ученим-монахом ще в 1136 році. І в цій праці вже використовувалися дробові числа Діти, як важливо знати історію свого народу і не втрачати зв'язок покоління. Тому, і сьогодні ми маємо вміти працювати з дробами, розширювати свої знання.

III. Актуалізація опорних знань учнів

1). (Відновити записи на дошці). Ми вивчаємо дроби. Поясніть запис

, a називається…, означає…

b називається …, означає…

2). Як записати відповідь дробом?

1 : 2=… , 7 : 9=…, 11 : 4=…, 5 : 3= …, 8 : 8 = ….

З останнього прикладу пригадуємо, як можна подати число 1 у вигляді дробу.

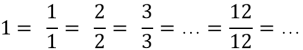
3). На минулому уроці ми порівнювали дроби.

4). Треба порівняти числа:

і.

IV. Пояснення теми

Для звичайних дробів розрізняють такі два випадки:

Чисельник звичайного дробу може бути меншим від знаменника.
Чисельник – може дорівнювати або бути більшим від знаменника.

Дріб, чисельник якого меншим від знаменника, називається правильним.

З попереднього завдання правильними дробами

Запишіть).

ПМК. Перегляд фрагменту 1 з уроку № 68.

Дріб, чисельник якого більший за знаменник або йому дорівнює, називають неправильним дробом.

З попереднього завдання неправильними дробами є: . (Запишіть).

ПМК. Перегляд фрагменту 2 з уроку №68.

А якщо порівняти правильний дріб з неправильним. Який дріб більший? (неправильний). Далі зобразимо дроби на координатному промені і порівняємо (завдання для візуалів та кінестетів біля дошки).

Зобразити правильні і неправильні дроби (чисельник яких менший за 16) із знаменником 6, якщо одиничний відрізок 6 клітинок.

Використаємо малюнок для порівняння:

V. Первинне закріплення знань

№999 (усно). (Коментують аудіали та візуали).

Навести приклади: 2 правильні дроби; 3 неправильні, один з яких дорівнює одиниці; (записати в зошитах та на дошці кінестети).

VI. Фізкультхвилинка

Всі піднесли руки –раз! На сусіда не дивись.

На носках стоїть весь клас, Будем дружно ми вставати,

Два – присіли, руки вниз, Щоб ногам роботу дати.

На сусіда подивись. Раз – присіли, два – піднялись.

Раз! – і вгору, Хто старався присідати,

Два! – і вниз, Може вже відпочивати.

VII. Розв’язування вправ

(Робота в парах)

На цьому етапі учні розв’язують вправи за підручником №1001, №1003, №1004, №1007, №1018 (скорочений запис умови).

Бригада побудувала склад – 72 дні, становить 1

Планом передбачено – ? днів, становить

Розв'язання

72 : 6 · 7 = 84 (дні).

Відповідь: 84 дні.

VIII. Підбиття підсумків

Учні звіряють відповіді, оцінюють один одного. Вчитель збирає зошити для корекції оцінок.

IX. Рефлексія

Який настрій від уроку?
Чи задоволені оцінками?

X. Домашнє завдання

Прочитати §30, вивчити правила, (диференційоване) №1008, №1011, №1019.

Урок №6

Тема. Мішані числа

Мета. Розширювати уявлення учнів про число, сформувати поняття «мішане число» та вміння записувати неправильні звичайні дроби у вигляді мішаних чисел, розвивати математичне мовлення, культуру записів, виховувати інтерес до процесу здобуття знань, активність, самооцінку.

Обладнання: ноутбук, ПМК “Математика навчального призначення”, 5 клас, автори Білоус Наталія та інші, підручник, дошка, картки завдань, кольорова крейда.

Хід уроку

I. Організаційний момент

Перевірка домашнього завдання.

( За зразком на дошці, або слайд. Самооцінка).

№1008.Порівняй дроби

1 ; 1; 1= ; 1; ; ;; ; = .

№1011

№1019

Фермер за планом – 18 т, становить 1

фактично –  т, становить

18: 9 · 10= 20 (т)

Відповідь: 20 т.

( Учні оцінюють свою роботу)

II. Мотивація навчальної діяльності: «Ми за здоровий спосіб життя».

ДІТИ!!! Цікаво знати,виявляється, що в 100 грамах вдихуваного повітря міститься 20 г кисню, а в 100 грамах видихуваного повітря міститься 16 г кисню. В якому повітрі більше кисню? На скільки? Чи можете ви розв’язати цю задачу? А як називають ці числа?

20, 16. Подивіться у «Модель майбутніх знань». Чи з усіма поняттями про звичайні дроби ви знайомі? Запишіть тему « Мішані числа».

III. Пояснення вчителя

На минулому уроці ми працювали з правильними та неправильними дробами. Неправильні дроби записують ще і по іншому у вигляді мішаних чисел. (Вчитель демонструє на слайді чи дошці за допомогою кольорової крейди)

Дріб неправильний. На промені його можна скласти з 1 цілої та додати дріб . Тому =1. Між цілою і дробовою частинами мішаного числа завжди розуміють дію додавання, але історично склалось так, що домовились знак «+» при цьому не писати. Кажуть що з неправильного дробу виділено цілу та дробову частини. Як з будь-якого неправильного дробу виділяти цілу і дробову частини. Прочитаємо правило на ст.227 (читає аудіал). Виконаємо перетворення за цим правилом:

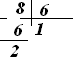
= 8 : 6 = 1

(запис у зошити)

Отримане число називають мішане. Приклади: 1; 21.

ПМК. Перегляд фрагментів 3,4 з уроку № 68.

Методична вказівка: (вчитель читає, повторюють аудіали (читання) і записують усі учні в зошити). Ці числа мають цілу та дробову частини. Взагалі для правильних дробів кажуть, що вони не мають цілої частини. Але не всі неправильні дроби мають дробову частину. Приклад неправильний дріб, але 14:14 = 1, або неправильний дріб, 18 : 3 = 6.

IV. Первинне закріплення знань

№ 1031, (аудіали), № 1032 (візуали), №1038 (візуали і кінестетики).

V. Фізкультхвилинка

Раз, два – руки в боки, Сім, вісім – розпрямись,

Три, чотири – два підскоки, Дев’ять, десять – всі присіли,

П’ять, шість – нахились, І за парти тихо сіли.

VI. Робота з картками за рівнями навчальних досягнень учнів

Методична вказівка: (вчитель на розсуд задає самостійну роботу за друкованими зошитами чи використовує картки.)

VII. Підбиття підсумків. Учні здають зошити.

VIII. Рефлексія

Про що цікаве дізналися на уроці? З чого складається запис мішаного числа? Як виділити цілу частину з неправильного дробу?
Який настрій від уроку?

IX. Домашнє завдання: читати §31, вивчити правило, №1039, №1045.

Урок №7

Тема. Додавання та віднімання звичайних дробів з однаковими

знаменниками

Мета: формувати навички додавання та віднімання дробів з однаковими знаменниками;розвивати навички науково-дослідницької роботи, логічне мислення; формувати пізнавальну та предметну компетентності.

Обладнання: ноутбук, ПМК “Математика навчального призначення” 5 клас автори Білоус Наталія та інші,підручник, ребус, набір моделей «Звичайні дроби», кольорова крейда.

Хід уроку

I. Організаційний момент

II. Мотивація навчальної діяльності учнів

(Використовую метод стимулювання інтелектуальної активності.)

Діти розгадайте ребуси  ( закодовані слова «додавання» та «віднімання).

Сьогодні темою уроку є «Додавання і віднімання звичайних дробів з однаковими знаменниками».

ребуси

III.Актуалізація опорних знань: (фронтальне опитування, вправа «Мікрофон»).

Як називають компоненти додавання?
Як називають компоненти дії віднімання?
Які закони для додавання ви знаєте?
Як знайти невідомий доданок?
Як знайти невідоме зменшуване?
Як знайти невідомий від’ємник?
Яку дію означає « більше на»?
Яку дію означає « менше на»?
Як записують звичайний дріб?
Як записують 1 неправильним дробом?
Як виділити цілу частину з неправильного дробу?

IV. Вивчення нового матеріалу

Створюю проблемну ситуацію.

Ситуація 1. На день народженні у ослика Іа Вінні-Пух з’їв торта , а П’ятачок з’їв торта. Яку частину торта з’їли разом Віні-Пух і П’ятачок?

(до дошки за бажанням викликаю візуала чи кінестетика). Пропоную продемонструвати на моделі «Звичайні дроби» розв’язання задачі).

А як записати дією: Діти, а хто спробує сформулювати правило додавання? (аудіали). Звіримо з підручником.

ПМК. Перегляд фрагменту 1 з уроку № 72.

Ситуація 2. Шоколадку розділену на дольки запропонували кенгуряткам. Кенгурятко Ласунчик взяло шоколадки, а Сонько шоколадки. Яка частинка шоколадки залишилась?

На дошці задачу із скороченою умовою розв’язує учень (візуал).

Ласунчик – частин

Сонько – частин Шоколадка – 1 ціла

Залишилось – ? частин

спосіб: 1) 1 – = 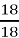– = ; 2 спосіб 1) + =

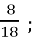
2) – = . 2) 1 – =

Відповідь:

Діти сформулюйте правило віднімання дробів з однаковими знаменниками.

ПМК. Перегляд фрагменту 2 з уроку № 72.

V. Первинне закріплення вивченого матеріалу (на дошці, або слайді)

+ ; ; + ; – ; – ; –

Якщо результатом є неправильний дріб,то прийнято виділяти цілу частину.

Ситуація 3. Діти, а як перевірити , що 1 = .

1спосіб (учні) 1 = + = .

2 спосіб (вчитель) Математичною мовою слід пояснювати так: ст.233

1 = =.

VI. Фізкультхвилинка

Петрик йшов, йшов, йшов Петрик йшов, йшов, йшов

(крокують на місці) І горішок знайшов.

І суницю знайшов. Підняв і далі пішов.

(нахиляються вперед) Петрик йшов, йшов, йшов

З’їв і далі пішов. І грибочок знайшов.

(імітація рухів, Поклав у кошик

які виконує хлопчик) І додому пішов. (сідають

за парти)

VII. Інтерактивне спілкування з учнями

Заповніть таблицю: (естафета)

а
в
а + в
а – в

Ситуація 4. Розв’язати рівняння

x + = ; + m = 1; a

VIII. Розв’язування вправ

№1082

IX. Мотиваційне оцінювання активної участі учнів на уроці

X. Рефлексія

Чи задоволені ви своїми успіхами?
Що було невдалим?Як перетворити мішане число у неправильний дріб?

XI. Домашнє завдання

Прочитати §32, вивчити правила додавання та віднімання, №1063,

(№1068), №1071 (№1080).

Урок №8

Тема. Додавання та віднімання звичайних дробів з однаковими знаменниками. Розв’язування вправ

Мета. Виробити міцні навички додавання та віднімання дробів з однаковими знаменниками; розвивати навички усного рахунку; формувати соціальну та предметну компетентності.

Обладнання: підручник, 5 клас, набір моделей «Звичайні дроби», кольорова крейда, ноутбук, проектор.

Хід уроку

I. Створення гарного настрою (обмін побажаннями)

Вчитель: « Доброго дня!Сьогодні такий сонячний морозний чудовий ранок! Я бажаю вам успіхів і найкращих оцінок на уроках.

Діти, розгадайте загадку:

На уроках, в книжці,в школі

Почерпнеш ти їх доволі

І назавжди у житті,

Стануть друзями тобі.

II. Сьогодні урок проведемо у вигляді змагання

Ви вже накопичили чимало знань про звичайні дроби Визначимо хто із вас заслуговує на звання «ЕРУДИТ». (Якщо кількість учнів менша за 10, або яка команда заслуговує на таке звання).

III. Правила змагань

За правильно розв’язане завдання учень або команда набирають певну кількість балів. В кінці уроку визначається переможець і нагороджується медаллю «ЕРУДИТ». (Завдання підібрані для учнів з різними каналами сприйняття інформації).

IV. Експрес-розминка (1 бал)

Щоб знайти суму дробів з однаковими знаменниками…
Щоб відняти дроби з однаковими знаменниками…
Сумою дробів 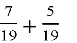є дріб …
Різницею дробів – є дріб…
Число 16 можна записати як суму цілого числа і дробу так…
Запишіть,що різницею дробів – 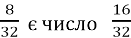. Перевірте цю рівність.
Сумою чисел числа 0 є число…

V. Задачі за готовою умовою (2 бали)

Задача 1

1 дня – частин лікарських трав

2 дня –частин лікарських трав

Задача 2

Полуницею –

Малиною – ? частин городу, на частини « < »

Капуста – ? частин городу, на « > »

Задача 3

Новорічні подарунки – 120 шт.

Дитячий садок – ?

Молодші класи –? шт.,

Залишилось – ? шт. (Запропонувати два способи розв’язання).

VI. Фізкультхвилинка

Всі ми звикли до порядку, Один і два, три і чотири –

Дружно робимо зарядку. Набираємося сили.

Ми на радість цьому дому Нахилились, повернулись,

Проганяєм сон і втому. До товариша всміхнулись.

І направо, і наліво, Щоб нічого не боліло.

VII. Пізнай самого себе

Розв’язування рівнянь . (3 бали).

( x + ) – = ; ( – y) + = (z – ) = .

VIII. Пік ерудита ( 5 балів)

Мама зранку дала донці 25 гривень кишенькових грошей. Ввечері донька розповіла, що усіх грошей вона витратила у шкільному буфеті, на жуйки, а за 8 гривень купила зошит. Мама зрозуміла, що донька витратила всі гроші. Як?

IX. Підбиття підсумків

Визначення учня (команди) переможця. Оцінювання учнів.

X. Рефлексія

Я на уроці…
Мені було …

ХІ. Домашнє завдання

Читати §32, вивчити правила додавання та віднімання, (диференційоване) №1063( №1068), №1071 (№1080).

Урок №9

Тема. Звичайні дроби. Урок систематизації та узагальнення знань

Мета. Узагальнити та систематизувати знання учнів з теми; відпрацювати вміння застосовувати їх до розв’язування вправ;

розвивати пізнавальну активність, зорову пам’ять, правильне математичне мовлення, свідомого сприймання матеріалу;

виховувати почуття взаємо відповідальності, взаємодопомоги, культуру діалогу.

Обладнання:ноутбук, дошка, плакати, крейда, саморобна модель “Звичайні дроби і координатний промінь”, картки із завданнями, “зашифроване слово“ із 7 букв закрите на дошці біля малюнка будинку.

Хід уроку

I. Організаційний момент (1 хв)

Зміна зошитів з домашніми завданнями.

Вчитель. Діти, наш урок сьогодні не звичайний. Ми проведемо його у вигляді гри. Ось правила. (Вчитель зачитує правила для (А), які записані на дошці. Їх можуть читати учні (В))

1. Бути тут і зараз. 2. Висловлювати думку.

3. Вміти слухати іншого. 4. Говорити по одному.

5. Бути активним. 6. Дарувати посмішку, настрій іншим.

Для полегшення спілкування з вчителем ви отримуєте конспект-опору.

Ну звичайно гра пройде у вигляді змагань між двома командами: 1 ряд – “Чисельник”, 2 ряд – “Знаменник”. При утворенні команд, учні мають змогу помінятися місцями (К).

За правильну відповідь на запитання команда отримує 1 бал.

II. Актуалізація опорних знань (4 хв)

1). Усний рахунок. Щоб визначити яка команда розпочинає гру першою, вчитель зачитує приклади (А), які записані на картках, картки отримує кожний учень (В):

=…; = = = = =

1 + 2 + = 2 ; 3 = ; = 4.

Отже, першою розпочинає змагання команда __________

2). Естафета. Даному малюнку знайти відповідний дріб на дошці і прикріпити малюнок. (Для (К). По одному члену команди підходять до вчителя, який роздає їм малюнки, учні кріплять їх на дошці.) Підведення підсумків цього конкурсу.

III. Мотивація (1 хв)

Ми будемо будувати із наших знань будинок. Він називається “Звичайний дріб”. (За технологією “Асоціативний кущ”).

IV. Робота в групах (7 хв)

Кожний будинок складається з певних елементів. Щоб їх не забути маємо назви: 1) фундамент; 2) східці; 3) стіни; 4) двері; 5) вікна; 6) дах; 7) громовідвід.

Щоб побудувати будинок дайте відповіді на такі запитання:

(Команди працюють по черзі, правильна відповідь – 1 бал).

1. (фундамент) Як записують звичайний дріб? Яку дію означає риска дробу? На що вказує знаменник дробу? На що вказує чисельник дробу? Приклади звичайних дробів (А).

2. (східці) Як записати 1 у вигляді звичайного дробу? Як записати будь яке натуральне число у вигляді звичайного дробу? (В)

3. (стіни)Які бувають дроби? Навести приклади правильних дробів.

Навести приклади неправильних дробів. Як розміщені на координатному промені дані дроби? (показати на моделі). Учні по черзі демонструють на моделі такі дроби:К)

4. (двері) Які правила порівняння звичайних дробів? (А)

5. (вікна) Як виділити цілу частину з неправильного дробу? Як перетворити мішане число в неправильний дріб? (А) Записати відповідну схему для прикладу 3. (В)

6. (дах) Як додавати (віднімати) дроби з однаковим знаменником (А). Записати відповідну схему для прикладів , 6 2 . ( В)

7. (громовідвід) Які задачі двох типів на дроби ми вчили? (В, К)

Висновки. От і збудували ми будинок під назвою “Звичайні дроби”. Будинок можна прикрашати і наповнювати зсередини. Тобто, нові знання про звичайні дроби ми отримаємо вже в 6 класі.

V. Фізкультхвилинка (1 хв)

Правильні дроби – присідаємо,

неправильні – руки вгору.

(Вчитель вимовляє дроби – учні здійснюють рухи).

VI. Робота в парах (20 хв)

Кожній парі учнів, що сидять за однією партою пропоную по два завдання. По завершенню роботи ми їх перевіримо.

Завдання першої пари (середній рівень), завдання другої пари (достатній рівень).

I пара

Допишіть таке число, щоб вийшла правильна нерівність:

Виконайте дії:

II пара

1. Розв’язати рівняння:

2. Розв’язати задачу.

У книзі 150 сторінок. Першого дня учень прочитав частини книги, а другого дня частини книги. Скільки сторінок учень прочитав за два дні?

По завершенням часу із команди-переможця в попередньому конкурсі, до дошки виходить учень з I пари і коментує 1 завдання. Всі учні слухають, записують і виправляють допущені помилки, якщо є потреба. Далі учень з команди суперника виконує 2 завдання. Аналогічно йде коментар завдань другої пари. Вчитель підводить підсумок цього етапу уроку.

VII. Командне тестування (7 хв)

На завершення уроку ми проводимо командне тестування за комп’ютером з теми “Звичайні дроби”. На комп’ютерах засіб ПМП “Математика” 5 клас. Урок №79. Тематична атестація. Одержані бали додаються до загальної кількості балів і визначається команда переможець.

ТЕСТИ „ЗВИЧАЙНІ ДРОБИ„

VIII. Підсумок уроку (2 хв)

Завершуємо наш урок. Сьогодні перемогла команда ____________ Ми повторили і систематизували матеріал з теми “Звичайні дроби”. Тепер нам буде легко написати контрольну роботу.

Я відмічаю активність таких учнів : _________.

IX. Рефлексія

А тепер поділіться своїми враженнями від уроку.
Який ваш настрій?
Що нового дізналися?
Що навчилися? (Лаконічні виступи учнів)

X. Домашнє завдання (1 хв)

Підготуватися до контрольної роботи. Повт. §27 – §32.

XI. (1 хв)

Нарешті дійшла черга розгадати зашифроване слово. Команда переможець має право відкрити 3 букви і назвати слово. Учні відгадують слово “РАДІСТЬ”.

Вчитель. Діти, я бажаю, щоб ви завжди відчували радість від навчання. Дякую за роботу, перерва.

Урок №10

Тема. Контрольна робота з теми «Звичайні дроби»

Мета. Перевірити рівень засвоєння учнями теми «Звичайні дроби»,

розвивати правильне математичне мислення, застосовувати набуті знання в різних ситуаціях; виховувати самостійність, вміння самоорганізуватися.

Обладнання: ноутбук, дошка, крейда, картки із завданнями .

Хід уроку

I. Організаційний момент (1 хв)

ІІ. Контрольна робота

Початковий рівень

1. Запиши у вигляді дробу число сім тринадцятих (1 бал) (А)

А) Б) В) Г)

2. Яким дробом можна виразити не зафарбовану частину фігури? (1 бал) (В)

А) Б) В) Г)

3.Яку частину години становлять 15 хвилин? (1 бал) (К)

А) Б) В) Г)

Середній рівень

4. З дробів вибери неправильні дроби (1 бал) (В)

Б) Г) .

5. Чому дорівнює найбільше натуральне значення p, за якого є правильна нерівність ? (1 бал) (А)

А) 4; Б) 5; В) 6; Г) 7.

6. У класі навчається 12 учнів. з низ взяли участь в математичному конкурсі «Кенгуру». Скільки учнів класу взяли участь в конкурсі «Кенгуру»? (1 бал) (К)

Достатній рівень

( 1,5 бал кожне завдання) (А і К)

7. Побудуйте координатний промінь та позначте на ньому точки А () і В (). Знайдіть відстань між точками А і В.

8. Розв’яжіть рівняння: (

Високий рівень

( 3 бали одне завдання на вибір)

9. При яких натуральних значеннях у, обидва дроби і неправильні? (А)

10. Розвязати задачу. Теплохід за течією річки йде зі швидкістю км/год. Швидкість течії 4 км/год. Скільки кілометрів пройде теплохід за 1 годину проти течії річки? (В і К)

Методичні вказівки

Пошук методів вимірювання рівня навчальних досягнень учнів на сучасному етапі набуває надзвичайної актуальності. Об’єктивні та точні методи вимірювання й оцінювання знань є однією з рушійних сил прогресу. Оцінювання якості математичної підготовки учнів здійснюються у двох аспектах:

Рівень оволодіння теоретичними знаннями та якість практичних умінь і навичок;
Здатність застосовувати вивчений матеріал під час розв’язування задач і вправ.

Використання тестів у навчальному процесі надійно входить у педагогічну практику.

При складанні контрольної роботи варто дотримуватися вимог визначених програмою з математики, а також враховувати природні здібності учнів з прицілом на канали сприйняття інформації. Учні 5 класу мають ще незначний обсяг уваги, тому тексти завдань треба формулювати лаконічно а кількість завдань така, щоб учні мали змогу підтвердити реальний рівень свої навчальних досягнень з теми.

У запропонованому варіанті контрольної роботи вказано бали за кожне завдання, а також передбачено кому найбільш рекомендовано такий вид завдань. Букви А, В, К умовно позначають:

А – «аудіал», В – «візуал», К – «кінестетик».

ІІІ. Домашнє завдання (1 хв)

Повторити §27 – §32.

Методика «Тип пам’яті»

Методика допоможе визначити тип пам’яті (зорова, слухова, моторно-слухова, комбінована).

Обладнання: чотири колонки слів записаних на окремих карточках.

1	2	3	4
вертоліт	літак	пароплав	вовк
лампа	чайник	собака	бочка
яблуко	метелик	парта	ковзани
олівець	ноги	чобітки	самовар
блискавка	ліс	сковорода	пилка
качка	автомобіль	сукня	загадка
обруч	свічка	гриб	Пальто
мельник	журнал	жарт	прогулянка
папуга	малина	калач	книжка
колонка	ремонт	дощ	велосипед

Інструкція проведення: експеримент проводиться в 4 етапи. На кожному етапі пропонується один стовпчик слів. Досліджуваний отримує завдання: запам’ятати якомога більше слів і за командою експериментатора записати слова на аркуші паперу.

На першому етапі експериментатор зачитує слова першого стовпчика. Інтервал між словами при читанні – 5 секунд, записати їх учень повинен після 10-секундної перерви закінчення читання всього стовпчика; потім відпочинок 10 хвилин.

На другому етапі учень впродовж хвилини читає про себе слова другого стовпчика. Записує ті слова, які зумів запам’ятати. Відпочинок 10 хвилин.

На третьому етапі експериментатор читає учневі слова 3-го стовпчика, а досліджуваний пошепки повторює кожне слово і «записує» їх в повітрі. Потім учень записує на аркуші слова, що запам’ятав. Відпочинок 10 хвилин.

На четвертому етапі експериментатор показує учневі слова четвертого стовпчика, читає йому їх. Досліджуваний повторює кожне слово пошепки, «записує» в повітрі. Потім записує на аркуші слова, що запам’ятав.

Обробка та аналіз результатів.

Проводиться перевірка правильності відтворення (порядок слів не важливий). Результати заносяться в таблицю.

Вид пам’яті	Кількість відтворених слів (а)	Коефіцієнт виду пам’яті С = а / 10
Слухова
Зорова
Моторно-слухова
Комбінована

Чим ближче коефіцієнт С до 1, тим краще розвинений відповідний вид пам’яті в учня.

Методика "Образна пам'ять",

або як відрізнити предмет від його зображення

Методика спрямована на вивчення короткочасної образної пам’яті.

У вигляді одиниці пам'яті використовують образ (зображення предмета, геометрична фігура, символ). Досліджуваному пропонується за 20 секунд запам'ятати максимальну кількість образів із запропонованої таблиці. Потім за 1 хв. він повинен відтворити ті образи, які запам'ятав (записати або намалювати).

Інструкція: "3араз я покажу тобі таблицю з малюнками. Намагайся запам'ятати якомога більше із намальованого. Після того, як я заберу таблицю, запиши або замалюй все, що встиг запам'ятати. Час представлення таблиці - 20 секунд".

Обробка та аналіз отриманих результатів.

Підраховується кількість правильно відтворених образів. В нормі – це 6 і більше відповідей.

Оцінка, бали	9	8	7	6	5	4	3	2	1
Кількість відтворених образів	15-16	13-14	10-12	7- 9	6	5	4	3	1-2

	2		В

Методика «Спостереження особливостей сприймання»

Залежно від особливостей сприймання і обробки інформації людей можна умовно розділити на 4 категорії:

Візуали – люди, які сприймають більшу частину інформації з допомогою зору.

Аудіали – ті, хто в основному отримує інформацію через слуховий канал.

Кінестетики – люди, які сприймають більшу частину інформації через другі органи відчуття (нюхові, дотику) і з допомогою рухів.

Дискрети – у них сприйняття інформації проходить в основному через логічне усвідомлення, з допомогою цифр, знаків, логічних висновків. Ця категорія є не чисельною, а школярам молодших класів взагалі не властивий даний тип сприймання.

Програма спостереження

Словник спілкування. Візуал в своїй мові використовує іменники, дієслова, прикметники, пов’язані в основному з зором (дивитися, спостерігати, картина, на перший погляд, прозорий, яскравий, як бачите і т. д.). Для аудіала характерно використання слів пов’язаних з слуховим сприйманням (голос, послухайте, обговорювати, мовчазний, тиша, голосний, милозвучний і т.д.). Словник кінестетика включає слова, які описують відчуття або рухи (хватати, м’який, теплий, дотик, гнучкий, чудовий нюх і т.д.).

Особливості уваги. Кінестетику взагалі важко концентрувати свою увагу і його можна відволікти чим завгодно; аудіал легко відволікається на звуки; візуалу шум майже не заважає.

Особливості запам’ятовування. Візуал пам’ятає те, що бачив, запам’ятовує картинками. Аудіал – те, що обговорював, запам’ятовує слухаючи. Кінестетик пам’ятає загальне враження, запам’ятовує рухаючись.

Поведінка під час перерви. Візуал найчастіше залишиться в класі, якщо більшість учнів виходить із нього. Для нього головне – можливість спокійно зануритись в свої зорові образи. Але йому можуть заважати шумні діалоги аудіалів або рухливі ігри кінестетиків. Тоді він вийде в коридор, де буде спостерігати за іншими дітьми або роздивлятиметься інформацію на стінах. Аудіали використовують перерву, щоб набалакатися і пошуміти. Особливо, якщо на попередньому уроці довелося «тримати рот на замку». Для кінестетика перерва потрібна, щоб порухатися, розім’ятися.

Яким чином записується домашнє завдання, якщо воно записано на класній дошці. Візуал слухняно відкриє щоденник і запише, правильніше, перепише з дошки те, що задано додому. Він надає перевагу мати потрібну інформацію, ніж запитувати у інших. Він легко сприймає її записану саме з дошки. Аудіал, якщо захоче записати домашнє завдання в школі, швидше за все, перепитає в сусіда по парті, що задано. На слух запише цю інформацію собі в щоденник. Вдома може «сісти за телефон» і дізнатися про те, що задано у однокласників. Кінестетик найчастіше довго риється у себе в портфелі, дістає звідти підручники, знаходить потрібні сторінки і прямо в підручниках обводить номера потрібних вправ.

Використані джерела

Актуальные проблемы нейропсихологии детского возраста / Под ред. Л.С. Цветковой. – М., 2001.
Антощук Є. В. Учимося запам'ятовувати і пригадувати. Швидка педагогічна допомога від української школи ейдетики «Мнемозина». – К.: Вирій, 2007.
Гриндер М. Исправление школьного конвейєра. – Нью-Йорк, 1989. [Електронний ресурс]. Режим доступу: http://www.koob.ru/grinder_ michael/righting_the_educational_conveyor.
Закон України «Про освіту». – Відомості Верховної Ради (ВВР, 2017, № 38-39, ст.380). [Електронний ресурс]. Режим доступу: http://zakon0.rada.gov.ua/laws/show/2145-19.
Істер О.С. Математика. Підручник для 5 класу загальноосвітніх навчальних закладів. – К.: Генеза, 2013. – 365 с.
Концепція нової української школи. [Електронний ресурс]. Режим доступу: https://mon.gov.ua/storage/app/media/zagalna%20serednya/nova-ukrainska-shkola-compressed.pdf.
Кочерга О. Психофізіологія творчості дітей. – К.: Шк. світ, 2011. – 128 с.
Кочерга О. Психофізіологія мозку дитини: асиметрія півкуль. [Електронний ресурс]. Режим доступу: http://ірро.оrg.ua/іndex.рhріd=1274&орtіоn=соm_соntent&task=view.
Сиротюк А. Л. Нейропсихологическое и психофизиологическое сопровождение обучения. – М.:ТЦ Сфера, 2003.
Сиротюк А. Л. Обучение детей с учетом психофизиологии. – М., 2000.
Сиротюк А. Л. Коррекция обучения и развития школьников. – М., 2001.
Цветкова Л. С. Методика нейропсихологической диагностики детей. – М., 2000.
Цимбалару А. Педагогічна інтерпретація індивідуальних особливостей молодших школярів у процесі взаємодії з об'єктами шкільного середовища // Завуч. – 2012. – № 11.
Шанина Т. Е. Упражнения специального кинезиологического комплекса для восстановления межполушарного взаимодействия у детей и подростков: Учеб. пособие. – М., 1999.

Для нотаток

docx

Завантажити

Зберегти на потім

Додав(-ла)

Кумайгородська Марія Андріївна

Пов’язані теми

Математика, 5 клас, Методичні рекомендації

Додано

7 листопада 2022

Переглядів

921

Оцінка розробки

Відгуки відсутні