"Фрактали" (для роботи в МАН)

ЗМІСТ

 

 

Вступ

1. Що таке фрак тали?
   1.    Поняття про фрактали
   2.    Історія виникнення фракталів

2.     Класифікація фракталів

3.   Види фракталів та методи їх створення
4.   Типи самоподібності у фракталах. Розмірність фракталів

2.   Використання фракталів в діяльності людини
   1.   Застосування фракталів у комп'ютерній  графіці
   2.   Застосування в фізиці та інших природничих науках
   3.   Стиснення зображень
   4.   Аналіз ринків
   5.   Інші застосування
      1.   Література
      2.   Радіотехніка та децентралізовані мережі

Висновок

Список літератури

ВСТУП

 

 

Обрана для дослідження тема є актуальною, адже все, що створено людиною, обмежено площинами. Коли зустрічається об’єкт у природі, то спочатку можна побачити, що описати його форму можна лише наближено й допоможуть в цьому фрактали. Де закінчуються правильні форми Евклідової геометрії, там зустрічаються фрактали.

Більшості людей здається , що геометрія в природі обмежується такими простими фігурами, як лінія , коло , конічний перетин , багатокутник, сфера , квадратична поверхня , а також їх комбінаціями.

Однак багато природні системи настільки складні і нерегулярні, що використання тільки знайомих об'єктів класичної геометрії для їх моделювання представляється безнадійним. Як наприклад, побудувати модель гірського хребта або крони дерева в термінах геометрії? Як описати те різноманіття біологічних конфігурацій, яке ми спостерігаємо в світі рослин і тварин ? Уявіть собі всю складність системи кровообігу, що з безлічі капілярів і судин  доставляє кров до кожної клітинки людського тіла. Уявіть, як хитромудро влаштовані легені та нирки, що нагадують за структурою дерева з гіллястою кроною.

Настільки ж складною та нерегулярної може бути і динаміка реальних природних систем. Як підступитися до моделювання каскадних водоспадів або турбулентних процесів, що визначають погоду?

Фрактали і математичний хаос - відповідні засоби для дослідження поставлених питань. Термін фрактал відноситься до деякої статичної геометричної конфігурації, такий як миттєвий знімок водоспаду. Хаос - термін динаміки, використовуваний для опису явищ, подібних турбулентному поведінки погоди. Нерідко те, що ми спостерігаємо в природі, інтригує нас нескінченним повторенням одного і того ж візерунка, збільшеного чи зменшеного у скільки завгодно разів . Наприклад, у дерева є гілки. На цих гілках є гілки трохи менше і т.д. Теоретично, елемент «розгалуження » повторюється нескінченно багато разів, стаючи все менше і менше. Те ж саме можна помітити, розглядаючи фотографію гірського рельєфу. Спробуйте трохи наблизити зображення гірської гряди - ви знову побачите гори. Так проявляється характерне для фракталів властивість самоподібності.

Фрактали оточують нас всюди: в природі, в комп'ютерних технологіях, їх використовують у науці, в економіці, в медицині. Теоретично, можна сказати, що все, що існує в реальному світі, є фракталом, будь то хмара або маленька молекула кисню. Без цього всього ми не уявляємо свого життя, але багато хто навіть не знають що таке «фрактал». Мене зацікавила ця тема, крім того я провела опитування серед учнів свого класу, і ніхто не зміг дати визначення поняттю «Фрактал». Тому я вирішила вивчити алгоритм побудови фракталів, познайомити з результатами своїх досліджень за проектом учнів 11-х класів, а згодом створити електронний навчальний посібник.

 

 

РОЗДІЛ 1

ЩО ТАКЕ ФРАКТАЛИ?

 

 

1. Поняття про фрактали

 

 

Фрактал - складна геометрична фігура, що володіє властивістю самоподібності, тобто складена з декількох частин, кожна з яких подібна всьому тілі цілком. У більш широкому сенсі під фракталами розуміють безлічі точок у евклідовому просторі, мають дробову метричну розмірність, або метричну розмірність, відмінну від топологічної. Тобто фрактал - це нескінченно самоподібна геометрична фігура, кожен фрагмент якої повторюється при зменшенні масштабу.

Слід зазначити, що слово "фрактал" не є математичним терміном і не має загальноприйнятого суворого математичного визначення. Воно може вживатися, коли розглянута фігура володіє якими-небудь з перерахованих нижче властивостей:

Володіє нетривіальною структурою на всіх масштабах. У цьому відмінність від регулярних фігур (таких, як окружність, еліпс,): якщо ми розглянемо невеликий фрагмент регулярної фігури в дуже великому масштабі, він буде схожий на фрагмент прямої. Для фрактала збільшення масштабу не веде до спрощення структури, на всіх шкалах ми побачимо однаково складну картину.

Є самоподібною або наближено самоподібною.

Володіє дробовою метричною розмірністю або метричною розмірністю, яка перевершує топологічну.

Багато об'єктів в природі мають фрактальними властивостями, наприклад, узбережжя, хмари, крони дерев, сніжинки, кровоносна система і система альвеол людини або тварин. Фрактали, особливо на площині, популярні завдяки поєднанню краси з простотою побудови за допомогою комп'ютера.

2.  Історія виникнення фракталів

 

 

 

Термін ″фрактал″ придумав у 1975р. французький математик Бенуа Мандельброт(1924-2010), використавши його в книзі «Фрактальна геометрія природи».
 Вчений народився у Варшаві, в 1936 році емігрував з родиною до Франції. Після початку війни був змушений переїхати на південь країни − м.Тюль, де пішов у школу. Згодом, завдяки неабияким здібностям до геометрії, Б.Мандельброт стає студентом Сорбонни. Після цього, переїхавши у США, він закінчує Каліфорнійський інститут технології. У 1952 р. отримав докторський ступінь в одному з університетів Парижа. В 1955 р. одружився з Альетт Каган і переїхав у Женеву. З 1958 Б.Мандельброт проживає і працює в США. Він займається теорією ігор, економікою, географією, астрономією, фізикою.
 У 1993р. стає лауреатом премії Вольфа з фізики ″ за усвідомлення широкого розповсюдження фракталів та розвиток математичних методів для їх опису; він змінив наш погляд на природу.″ У 2003 − лауреатом Премії Японії. 14 жовтня 2010р його не стало.

У середині 1960-х років Мандельброт розробив теорію так званої «фрактальної геометрії» або «геометрії природи». Її метою був аналіз зламаних, зморшкуватих та нечітких форм.В перекл. з лат. (fractus) - подрібнений, зламаний, розбитий. Одним з перших хто описав фрактали в 1918 році був французький математик Гастон Жюліа. Але в нього були відсутні будь-які зображення. Комп'ютери зробили видимим те, що не могло бути дослідженим за часів Жюліа.  Фрактали використовуються при аналізі та класифікації сигналів складної форми, що виникають у різних областях, наприклад, при аналізі коливань курсу валют в економіці, у фізиці твердого тіла, в динаміці активних середовищ, для стиснення зображень. 

РОЗДІЛ 2

КЛСИФІКАЦІЯ ФРАКТАЛІВ

 

 

1. Види фракталів та методи їх створення

 

 

Існують три поширені методи створення фракталів:

Перший метод — ітераційні функції, які будуються відповідно до фіксованого правила геометричних заміщень, в результаті яких утворюються геометричні фрактали, наприклад: сніжинка Коха (рис1).

Фрактали цього класу самі наочні. У двомірному випадку їх отримують за допомогою деякої ламаної або поверхні в тривимірному випадку, званої генератором. За один крок алгоритму кожен з відрізків, складових ламану, замінюється на ламану-генератор, у відповідному масштабі. В результаті нескінченного повторення цієї процедури, виходить геометричний фрактал. А також множина Кантора, килим Серпінського, трикутник Серпінського, крива Пєано, крива Коха, крива дракона, Т-Квадрат та губка Менгера є прикладами геометричних фракталів.

Розглянемо один з таких фрактальних об'єктів - триадную криву Кох. Побудова кривої починається з відрізка одиничної довжини (рис.2) - це 0-е покоління кривої Кох. Далі кожна ланка (в нульовому поколінні один відрізок) замінюється на який утворює елемент, позначений на рис.1 через n = 1. У результаті такої заміни виходить наступне покоління кривої Кох. У 1-му поколінні - це крива з чотирьох прямолінійних ланок, кожне завдовжки по 1/3. Для отримання 3-го покоління проробляються ті ж дії - кожна ланка замінюється на зменшений утворюючий елемент. Отже, для отримання кожного наступного покоління, всі ланки попереднього покоління необхідно замінити зменшеним створює елементом. Крива n-го покоління при будь-якому кінцевому n називається предфракталом. На рис.1 представлені п'ять поколінь кривої. При n прагне до нескінченності крива Кох стає фрактальним обьектом .

Для отримання іншого фрактального об'єкта потрібно змінити правила побудови. Нехай створює елементом будуть два рівних відрізка, з'єднаних під прямим кутом. У нульовому поколінні замінимо одиничний відрізок на цей утворюючий елемент так, щоб кут був зверху. Можна сказати, що при такій заміні відбувається зміщення середини ланки. При побудові наступних поколінь виконується правило: найперше ліворуч ланка замінюється на який утворює елемент так, щоб середина ланки зміщувалася вліво від напрямку руху, а при заміні наступних ланок, напрямки зсуву середин відрізків повинні чергуватися. На рис.3 представлені кілька перших поколінь і 11-е покоління кривої, побудованої по вищеописаному принципом. Гранична фрактальна крива (при n прагне до нескінченності) називається драконом Хартера-Хейтуея .

У машинній графіці використання геометричних фракталів необхідно при отриманні зображень дерев, кущів, берегової лінії. Двомірні геометричні фрактали використовуються для створення об'ємних текстур (малюнка на поверхні об'єкту )

Другий метод — рекурентні відношення, це фрактали, що визначаються рекурентним відношенням у кожній точці простору (такому як площина комплексних чисел). Отримані таким методом фрактали називають алгебраїчними.

Прикладами алгебраїчних фракталів є множина Мандельброта (рис.4), палаючий корабель та фрактал Ляпунова.

Це найбільша група фракталів . Отримують їх за допомогою нелінійних процесів в n - мірних просторах. Найбільш вивчені двомірні процеси . Інтерпретуючи нелінійний ітераційний процес, як дискретну динамічну систему, можна користуватись термінологією теорії цих систем : фазовий портрет, сталий процес , аттрактор і т.д.

В якості прикладу розглянемо множину Мандельброта (pис.4 і рис.5). Алгоритм його побудови досить простий і заснований на простому ітеративному вираженні:

 

Z [i +1] = Z [i] * Z [i] + C,

 

де Zi і C - комплексні змінні. Ітерації виконуються для кожної стартової точки C квадратної або прямокутної області - підмножині комплексній площині. Ітераційний процес продовжується до тих пір, поки

Z [i] не вийде за межі кола радіуса 2, центр якої лежить у точці (0,0), (це означає, що аттрактор динамічної системи знаходиться в нескінченності), або після досить великого числа ітерацій (наприклад 200-500) Z [i] зійдеться до якої-небудь точці кола. Залежно від кількості ітерацій, в перебігу яких Z [i] залишалася всередині кола, можна встановити колір точки C (якщо Z [i] залишається всередині кола протягом досить великої кількості ітерацій, ітераційний процес припиняється і ця точка растра забарвлюється в чорний колір) .

Відомо , що нелінійні динамічні системи володіють кількома стійкими станами . Той стан , в якому опинилася динамічна система після деякого числа ітерацій , залежить від її початкового стану . Тому кожне стійкий стан (або як кажуть - аттрактор ) володіє деякою областю початкових станів , з яких система обов'язково потрапить в розглянуті кінцеві стану . Таким чином фазовий простір системи розбивається на області тяжіння аттракторов . Якщо фазовим є двомірний простір , то забарвлюючи області тяжіння різними кольорами , можна отримати кольоровий фазовий портрет цієї системи ( ітераційного процесу). Міняючи алгоритм вибору кольору , можна отримати складні фрактальні картини з химерними кольоровими візерунками . Несподіванкою для математиків стала можливість за допомогою примітивних алгоритмів породжувати дуже складні нетривіальні структури .

Вищеописаний алгоритм дає наближення до так званого безлічі Мандельброта. Безлічі Мандельброта належать точки, які протягом бесконечногочісла ітерацій не йдуть у нескінченність (точки мають чорний колір). Точки належать границі безлічі (саме там виникає складні структури) йдуть у нескінченність за кінцеве число ітерацій, а точки лежать за межами безлічі, йдуть у нескінченність через декілька ітерацій (білий фон).

Третій метод — випадкові процеси, це фрактали, що генеруються з використанням стохастичних, а не детермінованих процесів, наприклад: фрактальні ландшафти (мал.6 а,б,в,г,д), траєкторія Леві та броунівське дерево.

Ще одним відомим класом фракталів є стохастичні фрактали, які виходять у тому випадку, якщо в ітераційному процесі випадковим чином змінювати будь-які його параметри. При цьому виходять об'єкти дуже схожі на природні - несиметричні дерева, порізані берегові лінії і т.д. Двовимірні стохастичні фрактали використовуються при моделюванні рельєфу місцевості і поверхні моря .

 

2.  Типи самоподібності у фракталах. Розмірність фракталів

 

 

Розрізняють три типи самоподібності у фракталах:

Точна самоподібність — це найсильніший тип самоподібності; фрактал виглядає однаково при різних збільшеннях. У фракталів, згенерованих з використанням ітераційних функцій, часто виявляється точна самоподібність.

Майже самоподібність — слабка форма самоподібності; фрактал виглядає приблизно (але не точно) самоподібним при різних збільшеннях. Майже самоподібні фрактали містять малі копії цілого фракталу у перекручених та вироджених формах. Фрактали, згенеровані з використанням рекурентних відношень, зазвичай є майже (але не точно) самоподібними.

Статистична самоподібність — це найслабкіша форма самоподібності; фрактал має чисельні або статистичні міри, що зберігаються при збільшенні. Найприйнятніші означення "фракталів" просто містять в собі деякий вид статистичної самоподібності (розмірність фракталу, саме по собі, є чисельною мірою, що зберігається при збільшенні). Ймовірнісні фрактали є прикладами фракталів, які є статистично, але не майже й не точно самоподібними.

У евклідової геометрії є поняття розмірності: розмірність крапки — нуль, відрізка та кола — одиниця, круга і сфери — два, кулі — три. З одновимірними об'єктами ми пов'язуємо поняття довжини, з двовимірними - площі і так далі. Але як можна уявити собі множину з розмірністю 3/2? Мабуть, для цього потрібно щось проміжне між довжиною і площею, і якщо довжину умовно назвати 1-мірою, а площа - 2-мірою, то потрібна (3/2) -міра.

У 1919 році Ф. Хаусдорф дійсно визначив таку а-міру і на цій основі кожній множині в евклідовому просторі підставив число, назване їм метричною розмірністю. Він же навів перші приклади множин з дробовою розмірністю. Виявилось, що дробову розмірність мають канторова множина, крива Коха і інші екзотичні об'єкти, до недавнього часу маловідомі за межами математики.

Оскільки фрактал складається з нескінченного числа елементів, що повторюються, неможливо точно виміряти його довжину. Це означає, що чим точнішим інструментом ми будемо його вимірювати, тим більшою виявиться його довжина. Тоді як гладка евклідова лінія заповнює в точності одновимірний простір, фрактальна лінія виходить за межі одновимірного простору, вторгаючись у двовимірне. Таким чином, фрактальна розмірність кривої Коха знаходитиметься між 1 і 2. Найдивовижнішим виявляється те, що й багато природних об'єктів володіють ніби дробовою розмірністю, хоча, відверто кажучи, для природних об'єктів таку розмірність обчислити неможливо. Правильніше сказати, що в певних діапазонах спостереження природні об'єкти, що виникли в результаті довгої дифузії й абсорбції, схожі на фрактальні множини. Наприклад, розмірність побережжя лежить між 1,01 і 1,6, а кровоносної системи людини — між 3,4 і 3,6.

 

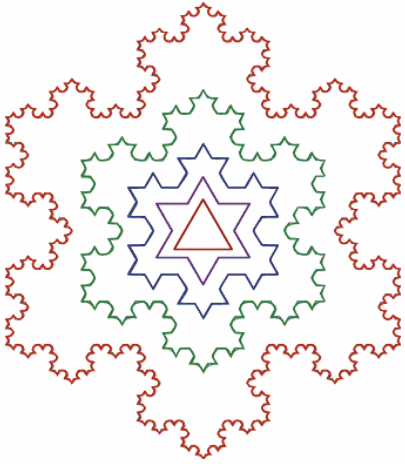
Рис.1

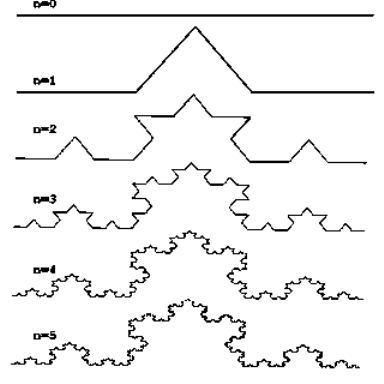
Рис.2

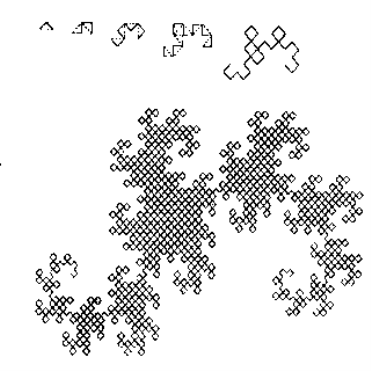
Рис.3

 

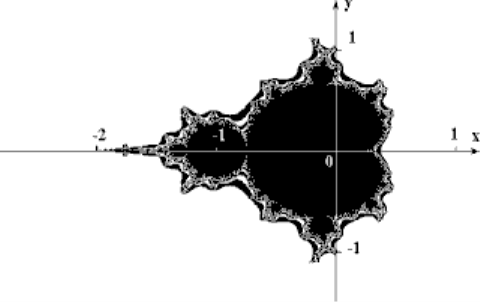
Рис.4

Рис.5

 

 

 

Рис.6(а,б)

Рис.6(в.г,д)

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 3

ВИКОРИСТАННЯ ФРАКТАЛІВ В ДІЯЛЬНОСТІ ЛЮДИНИ

 

 

          3.1 Застосування фракталів у комп'ютерній  графіці

Фрактали широко застосовуються в комп'ютерній графіці для побудови зображень природних об'єктів, таких, як дерева, кущі, гірські ландшафти, поверхні морів і так далі.

З використанням фракталів можуть будуватися не тільки ірреальні зображення, але і цілком реалістичні. Наприклад, фрактали нерідко використовуються при створенні хмар, снігу, берегових ліній, дерев і кущів та ін.. Тому застосовувати фрактальні зображення можна в самих різних сферах, починаючи від створення звичайних текстур і фонових зображень і закінчуючи фантастичними ландшафтами для комп'ютерних ігор або книжкових ілюстрацій. А створюються подібні фрактальні шедеври (так само як і векторні) шляхом математичних розрахунків, але на відміну від векторної графіки базовим елементом фрактальної графіки є сама математична формула - це означає, що ніяких об'єктів в пам'яті комп'ютера, не зберігається, і зображення будується виключно на основі рівнянь.

 

 

 

 

 

 

 

 

 

 

3.2 Застосування в фізиці та інших природничих науках

У фізиці фрактали природним чином виникають при моделюванні нелінійних процесів, таких, як турбулентний плин рідини, складні процеси дифузії-адсорбції, полум'я, хмари і інше. Фрактали використовуються при моделюванні пористих матеріалів, наприклад, в нафтохімії. У біології вони застосовуються для моделювання популяцій і для опису систем внутрішніх органів (система кровоносних судин). рівнянь.

3.3 Стиснення зображень

 

 

Фрактальний стиск зображень - це алгоритм стиснення зображень з втратами, заснований на застосуванні систем ітеріруємих функцій  до зображень. Даний алгоритм відомий тим, що в деяких випадках дозволяє отримати дуже високі коефіцієнти стиснення для реальних фотографій природних об'єктів, що недоступно для інших алгоритмів стиснення зображень в принципі. Через складну ситуацію з патентуванням широкого розповсюдження алгоритм не отримав.

Основа методу фрактального кодування - це виявлення самоподібних ділянок в зображенні. Вперше можливість застосування теорії систем ітеріруемих функцій ( IFS ) до проблеми стиснення зображення була досліджена Майклом Барнслі  і Аланом Слоуном. Вони запатентували свою ідею в 1990 і 1991 рр.. Джеквін представив метод фрактального кодування , в якому використовуються системи доменних і рангових блоків, блоків квадратної форми , що покривають все зображення. Цей підхід став основою для більшості методів фрактального кодування , застосовуваних сьогодні. У відповідності з даним методом зображення розбивається на безліч рангових підзображень , що не перекриваються і визначається безліч доменних під зображень, що перекриваються . Для кожного рангового блоку алгоритм кодування знаходить найбільш підходящий доменний блок і афінне перетворення , яке переводить цей доменний блок в даний ранговий блок . Структура зображення відображається в систему рангових блоків , доменних блоків і перетворень.

Ідея полягає в наступному: припустимо що вихідне зображення є нерухомою точкою якогось стискає відображення  Тоді можна замість самого зображення запам'ятати будь-яким чином це відображення, а для відновлення досить багато разів застосувати це відображення до будь-якого стартового зображенню.

За теоремою Банаха, такі ітерації завжди призводять до нерухомої точці , тобто до вихідного зображення . На практиці вся складність полягає у знаходженні по зображенню найбільш відповідного стискає відображення і в компактному його зберіганні. Як правило, алгоритми пошуку значною мірою переборні і вимагають великих обчислювальних витрат . У той же час, алгоритми відновлення досить ефективні і швидкі.

Основна складність фрактального стиснення полягає в тому , що для знаходження відповідних доменних блоків взагалі кажучи потрібен повний перебір. Оскільки при цьому переборі щоразу повинні порівнюватися два масиви, дана операція виходе й достатньо тривалою .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.4 Аналіз ринків

 

 

Останнім часом фрактали стали популярним інструментом у трейдерів для аналізу стану біржових ринків . Фрактали ринку є одним з індикаторів в торговельній системі Біла Вільямса . Вважається , що він же вперше і ввів цю назву в трейдинг . При торгівлі по фракталах , у поєднанні зі своїм індикатором Алігатор , автор виявляв локальні максимуми або мінімуми ринку .

Теорія фракталів на ринку у свій час викликала бурхливі суперечки , перш за все, тому що автор , як вважають багато хто, вставив у свою теорію багато наукової термінології ( фрактал , аттрактор і т.д.) , і зробив це не зовсім коректно . Оскільки фрак тали Вілямса з'являються на ринку досить часто і практично на всіх тимчасових таймфреймах і є , по суті , простими локальними екстремумами на відрізку з 5 барів і практично не відповідають математичної теорії фракталів . Точно таким же освітою на графіку є і ТД - точки другого порядку Томаса Демарка . Однак , незважаючи всі ці збіги це теорія дуже популярна і досі .

Зовсім не обов'язково щоб барів було п'ять ( 5 - мінімальна кількість барів для формування фрактала на ринку) і щоб , наприклад , для фрактала вгору максимуми , починаючи від центрального ( самого вищого) бару послідовно знижувалися. Так само необов'язковою умовою є те , що у центрального бару фрактала "вгору" мінімум , як і максимум , був вище за інших.

Якщо у формації два бари мають максимуми і обидва ці максимуму найвищі , то другий максимальний бар не враховується в розрахунках при торгівлі по фракталах . Те ж саме стосується і мінімумів для фрактала вниз.

Проривом покупців у Біла Вільямса вважається вихід ціни за переділи фрактала вгору хоча б на один пункт. Відповідно проривом продавців вважається вихід ціни за межі фрактала вниз хоча б на один пункт. Класично, за Білу Вільямсу фрактал використовують для проривний стратегії , хоча в технічному аналізі є й зворотні контртрендовие стратегії , які використовують схожі шаблони цен.Прориви покупців і продавців є безпосередніми торговими сигналами , тобто трохи вище фрактала вгору ставиться ордер на покупку , ордер на продаж ставиться трохи нижче фрактала вниз. При такій стратегії торгівлі по фракталах ордер стоп-лосс (Stop - Loss ) ставиться на самому віддаленому фрактальному екстремумі з двох останніх фракталів , спрямованих у протилежний бік . Зазвичай (але не завжди ) це передостанній протилежний фрактал . Наприклад , стоп-лосс (Stop - Loss ) для позиції на покупку ставиться на найнижчому з двох останніх фракталів , відповідно стоп-лосс для на позицію на продаж ставиться на найвищому з двох останніх фракталів вгору.

В системі Вільямса фрактал на ринку використовується не окремо , а в поєднанні з індикатором Алігатор . При цьому певний напрям і Алігатора і фрактала є обов'язковими прийнятті рішення про операцію. Наприклад, угода при пробитті фрактала вгору здійснюється , тільки якщо фрактал знаходиться вище Зубов Алігатора . А угода на продаж здійснюється , тільки якщо фрактал знаходиться нижче Зубів Алігатора . Таким чином , фрактал і Алігатор є двома підтверджуючими один одного індикаторами .

 

3.5 Інші застосування

 

3.5.1 Література

Серед літературних творів знаходять такі , які володіють текстуальної , структурної або семантичної фрактальної природою. У текстуальних фракталах потенційно нескінченно повторюються елементи тексту:

Нескінченне дерево , тотожне саме собі з будь ітерації ( « У попа була собака ... » , «Притча про філософа , якому сниться , що він метелик , якому сниться , що він філософ , якому сниться ... » , « Помилково твердження, що істинно твердження , що хибно твердження ... »)

У структурних фракталах схема тексту потенційно фрактальна :

вінок сонетів ( 15 віршів ) , вінок вінків сонетів ( 211 віршів ) , вінок вінків вінків сонетів ( 2455 віршів )

« Оповідання в оповіданні » (« Книга тисячі і однієї ночі» , Я. Потоцький «Рукопис , знайдений у Сарагосі » )

Передмови , що приховують авторство ( У. Еко «Ім'я троянди » )

Т. Стоппард « Розенкранц і Гільденстерн мертві » (сцена з поданням перед королем ) .

У семантичних і наративних фракталах автор розповідає про нескінченному подобі частини цілому :

Х. Л. Борхес «У колі руїн »

Х. Кортасар « Жовта квітка »

Ж. Перек « Кунсткамера »

3.5.2 Радіотехніка та децентралізовані мережі

Використання фрактальної геометрії при проектуванні антенних пристроїв було вперше застосовано американським інженером Натаном Коеном, який тоді жив у центрі Бостона, де була заборонена установка зовнішніх антен на будівлі. Натан вирізав з алюмінієвої фольги фігуру у формі кривої Коха і наклеїв її на лист паперу, потім приєднав до приймача. Виявилося, що така антена працює не гірше звичайного. І, хоча фізичні принципи роботи такої антени не вивчені досі, це не завадило Коену заснувати власну компанію і налагодити їх серійний випуск.

Система призначення IP-адрес в мережі Netsukuku використовує принцип фрактального стиснення інформації для компактного збереження інформації про вузли мережі. Кожен вузол мережі Netsukuku зберігає всього 4 Кб інформації про стан сусідніх вузлів, при цьому будь-який новий вузол підключається до загальної мережі без необхідності в центральному регулюванні роздачі IP-адрес, що, наприклад, характерно для мережі Інтернет. Таким чином, принцип фрактального стиснення інформації гарантує повністю децентралізовану, а отже, максимально стійку роботу всієї мережі.

 

ВИСНОВОК

 

 

Фрактал є однією з багатьох складових частин певної субстанції, тому зникнення однієї з таких складових призводить до втрати візуальної гармонії, що людське око розпізнає одразу. Присутність фрактала з першого погляду можна і не помітити, якщо не заглиблюватись у досконале вивчення математики. Ця наука, дійсно, не має меж і постійно спонукає до різноманітних досліджень.

Фрактал — це математична величина, що зустрічається досить часто. Але якщо добре не придивитися, його можна і не побачити. Абсолютно точна, алгебраїчна величина, яка творить собою неймовірні фігури, візерунки та складає цікаві орнаменти, що ми зустрічаємо кожного дня. Це і листя папороті, і маленькі сніжинки та ще багато іншого.

Галілео Галілей у 1623 році писав: “Вся наука записана у цій великій книзі, — я маю на увазі Всесвіт, — що завжди відкрита для нас, але яку неможливо зрозуміти, не навчившись розуміти мову, на якій вона написана, а написана вона на мові математики, і її літерами є трикутники, кола і інші геометричні фігури, без яких людині не можливо розібрати жодного її слова; без них вона подібна блукаючому в пітьмі…”

Поняття фрактала змінило багато традиційних уявлень про геометрію, а в історії розвитку математики введення цього поняття стало переломним моментом. З кожним роком поняття фрактала стає відоме все більш широкому колу людей. І зараз цей термін важко залишити без належної уваги. У природі є багато чого, що має прямий зв’язок до цього терміну.

Займаючись цією темою, я більш широко дізналася про об’єкт дослідження: його властивості, способи створення та використання. З алгебраїчних фракталів я звернула увагу на множину Мандельброта, дракон Хартера-Хейтуея, які відрізняються один від одного за побудовою та своїми загальними формулами створення, на мою думку, найбільше досліджені в наш час. За допомогою їх з’являється більшість новостворених фракталів.

Сподіваюсь, що і після закінчення школи, у мене залишиться велике бажання продовжити досліджувати загальні формули побудови фракталів і за допомогою цих формул створювати нові фрактали та захоплюватися їхньою незрівнянною красою.

 

СПИСОК ЛІТЕРАТУРИ

 

 

1.  Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002.
2. Фоменко А. Т. Наглядная геометрия и топология. — М.: изд-во МГУ, 1993.
3.  Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М.: «Мир», 1993.
4. Фракталы в физике. Труды 6-го международного симпозиума по фракталам в физике, 1985. — М.: «Мир», 1988.
5. Федер Є. Фрактали. - М: "Мир", 1991.