Функція. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції
Тема уроку. Функція. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції
Мета уроку: сформувати знання учнів про нулі функцій, проміжки знакосталості, проміжки спадання, зростання функції; навчити знаходити нулі функції, проміжки знакосталості, досліджувати функцію на зростання, спадання; розвивати увагу, пам’ять, уміння аналізувати; виховувати працьовитість, дисциплінованість.
Очікувані результати: учні повинні вміти знаходити нулі функції, проміжки знакосталості, досліджувати функцію на зростання, спадання.
Тип уроку: урок засвоєння нових знань.
Хід уроку
■ I. Організаційний етап
▪ Привітання
▪ Перевірка готовності учнів та кабінету до уроку
■ II. Перевірка домашнього завдання
▪ Перевірка письмового завдання біля дошки
▪ Математичний диктант
1. Знайдіть значення функції ![]() , якщо
, якщо ![]() .
.
2. Укажіть область визначення функції ![]() .
.
3. Укажіть область значень функції ![]() .
.
4. Функцію задано формулою ![]() . Знайдіть
. Знайдіть ![]() .
.
5. Функцію задано формулою ![]() . Знайдіть значення аргумента, якщо значення функції дорівнює 1.
. Знайдіть значення аргумента, якщо значення функції дорівнює 1.
6. Знайдіть область визначення функції ![]() .
.
Відповіді до математичного диктанту
1. 1. 2. Всі дійсні числа. 3. Множина невід’ємних чисел. 4. 3. 5. 0. 6. ![]() .
.
Запропонувати учням здійснити самоперевірку за відповідями, заздалегідь підготовленими на відкидній дошці.
■ III. Формулювання мети й завдань уроку, мотивація навчальної діяльності
▪ Оголошення теми уроку
▪ Формулювання разом з учнями мети й завдань уроку
▪ Мотивація навчальної діяльності
Сьогодні ми познайомимося з властивостями функції, що дозволить говорити про функції в ширшому значенні, будемо вчитися застосовувати властивості функції під час розв’язування задач.
 ■ IV. Актуалізація опорних знань
■ IV. Актуалізація опорних знань
▪ Фронтальне опитування
1. Розв’яжіть рівняння:
а) ![]() ; б)
; б) ![]() .
.
2. Розв’яжіть нерівність:
а) ![]() ; б)
; б) ![]() .
.
3. За якого значення аргумента x ![]() ?
?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
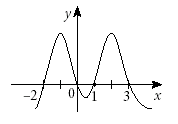
4. Знайдіть координати точок перетину графіка функції ![]() з віссю абсцис (див. рисунок).
з віссю абсцис (див. рисунок).
■ V. Засвоєння нових знань
План викладання нового матеріалу
1. Нулі функції. Проміжки знакосталості.
2. Зростання та спадання функції.
3. Приклади розв’язування вправ.
1. Нулі функції. Проміжки знакосталості.
Значення аргумента, при якому значення функції дорівнює нулю, називають нулем функції.
Щоб знайти нулі функції ![]() , потрібно розв’язати рівняння
, потрібно розв’язати рівняння ![]() .
.
Розглянемо функцію ![]() , графік якої зображено на рисунку.
, графік якої зображено на рисунку.
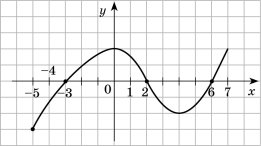
Нулями цієї функції є числа –3, 2, 6. Зауважимо, що на проміжках ![]() і
і ![]() графік розташований над віссю абсцис, а на кожному з проміжків
графік розташований над віссю абсцис, а на кожному з проміжків ![]() і
і ![]() — під віссю абсцис, тобто на кожному з проміжків
— під віссю абсцис, тобто на кожному з проміжків ![]() і
і ![]() функція набуває лише додатних значень, а на кожному з проміжків
функція набуває лише додатних значень, а на кожному з проміжків ![]() і
і ![]() — тільки від’ємних значень. Кожен із зазначених проміжків є проміжком знакосталості функції f.
— тільки від’ємних значень. Кожен із зазначених проміжків є проміжком знакосталості функції f.
Таким чином, кожен із проміжків, на якому функція набуває значень того самого знака, називають проміжком знакосталості функції f.
2. Зростання і спадання функції.
Розглянемо графік функції, наведений на рисунку. На проміжку ![]() графік «іде вгору»: зі збільшенням значень аргумента із цього проміжку відповідні значення функції збільшуються. Тоді кажуть, що на проміжку
графік «іде вгору»: зі збільшенням значень аргумента із цього проміжку відповідні значення функції збільшуються. Тоді кажуть, що на проміжку ![]() функція зростає.
функція зростає.
Функція f зростає на певному проміжку, якщо для будь-яких двох значень аргумента з цього проміжку більшому значенню аргумента відповідає більше значення функції.
Функція f спадає на певному проміжку, якщо для будь-яких двох значень аргумента з цього проміжку більшому значенню аргумента відповідає менше значення функції.
Якщо функція зростає на всій області визначення, то її називають зростаючою, аналогічно, якщо функція спадає на всій області визначення, то її називають спадною.
Наприклад, зростаючими є функції ![]() ,
, ![]() ; спадними — функції
; спадними — функції ![]() ,
, ![]() .
.
3. Приклади розв’язування вправ.
Розглянемо декілька прикладів.
1) Знайдемо нулі функції ![]() .
.
Розв’язання
Розв’яжемо рівняння ![]() ;
; ![]() Отже, функція має два нулі:
Отже, функція має два нулі: ![]() ;
; ![]() .
.
Відповідь: 3; 6.
2) Доведемо, що якщо ![]() , то функція
, то функція ![]() є зростаючою, а якщо
є зростаючою, а якщо ![]() — спадною.
— спадною.
Доведення
Нехай ![]() і
і ![]() — довільні значення аргумента, причому
— довільні значення аргумента, причому ![]() . Позначимо через
. Позначимо через ![]() і
і ![]() відповідні їм значення функції.
відповідні їм значення функції. ![]() і
і ![]() . Розглянемо різницю
. Розглянемо різницю ![]() :
: ![]()
![]() .
. ![]() , оскільки
, оскільки ![]() , тому знак добутку
, тому знак добутку ![]() визначається знаком коефіцієнта k. Якщо
визначається знаком коефіцієнта k. Якщо ![]() , то
, то ![]() і
і ![]() , отже, якщо
, отже, якщо ![]() , функція
, функція ![]() є зростаючою.
є зростаючою.
Якщо ![]() , то
, то ![]() і
і ![]() . Якщо
. Якщо ![]() , функція
, функція ![]() є спадною, що і треба було довести.
є спадною, що і треба було довести.
■ VI. Первинне закріплення знань
▪ Усні завдання
Підручник ___________________________________________________
▪ Робота учнів біля дошки
Підручник ___________________________________________________
Дидактичні матеріали
▪ Індивідуальна робота за картками
Картка 1
1. Знайдіть нулі функції:
а) ![]() ; б)
; б) ![]() .
.
2. При якому найбільшому цілому значенні а функція ![]() є зростаючою?
є зростаючою?
3. Знайдіть проміжки знакосталості функції ![]() .
.
Картка 2
1. При яких значеннях а функція ![]() є спадною?
є спадною?
2. Доведіть, що функція ![]() спадає на проміжку
спадає на проміжку ![]() .
.
3. При яких значеннях а функція ![]() має два нулі?
має два нулі?
Розв’язання та відповіді до карток
Картка 1
1. а) ![]() ;
;
![]() :
: ![]() ;
;
![]() .
.
![]() ;
; ![]()
![]()
![]() — нуль даної функції.
— нуль даної функції.
Відповідь: 1.
б) ![]() ;
;
![]() ;
; ![]()
![]()
![]() — нуль даної функції.
— нуль даної функції.
Відповідь: 4.
2. ![]() .
.
Функція зростає, якщо ![]() ,
, ![]() ;
; ![]() . Найбільше ціле значення:
. Найбільше ціле значення: ![]() .
.
Відповідь: 2.
3. ![]() . Якщо
. Якщо ![]() , то
, то ![]() ;
; ![]() ;
; ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Відповідь: ![]() при
при ![]() ;
; ![]() при
при ![]() .
.
Картка 2
1. ![]() .
.
![]() . Функція спадна, якщо
. Функція спадна, якщо ![]() , тобто при
, тобто при ![]() .
.
Відповідь: при ![]() .
.
2. Нехай ![]() і
і ![]() — довільні значення аргумента з проміжку
— довільні значення аргумента з проміжку ![]() , причому
, причому ![]() . Покажемо, що
. Покажемо, що ![]() . Маємо:
. Маємо: ![]() , тоді
, тоді ![]() . Обидві частини останньої нерівності є невід’ємними числами, отже,
. Обидві частини останньої нерівності є невід’ємними числами, отже, ![]() , тобто
, тобто ![]() .
.
3. ![]() .
.
Два нулі функція матиме, якщо ![]() .
.
![]()
![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
Відповідь: при ![]() .
.
Перевірити й оцінити робіти учнів.
■ VII. Підбиття підсумків уроку
▪ Бесіда
 1. Яке значення аргумента називають нулем функції?
1. Яке значення аргумента називають нулем функції?
2. Що називають проміжком знакосталості функції?
3. Яку функцію на певному проміжку називають зростаючою; спадною?
4. Яку функцію називають зростаючою; спадною?
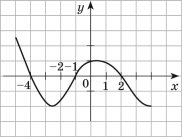
5. На рисунку зображено графік ![]() , визначений на множині дійсних чисел.
, визначений на множині дійсних чисел.
Користуючись графіком, знайдіть:
а) нулі функції;
б) значення аргумента, за яких значення функції додатні; від’ємні;
в) проміжки зростання та спадання функції.
■ VIII. Домашнє завдання, інструктаж щодо його виконання
▪ Завдання для всього класу
Підручник __________________________________________________
Дидактичні матеріали
▪ Індивідуальне завдання
При яких значеннях а функція ![]() має тільки один нуль?
має тільки один нуль?
Розв’язання
Якщо ![]() ,
, ![]() , то функція буде лінійною і матиме тільки один нуль.
, то функція буде лінійною і матиме тільки один нуль.
Якщо ![]() ,
, ![]() , то функція матиме тільки один нуль,
, то функція матиме тільки один нуль, ![]() .
.
![]()
![]() ;
; ![]() ;
; ![]()
Відповідь: при ![]() ; 1,5; 2.
; 1,5; 2.
|
Картка 1 1. Знайдіть нулі функції:
а)
2. При якому найбільшому цілому значенні а функція
3. Знайдіть проміжки знакосталості функції
|
|
Картка 2
1. При яких значеннях а функція
2. Доведіть, що функція
3. При яких значеннях а функція
|


про публікацію авторської розробки
Додати розробку
