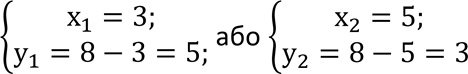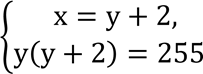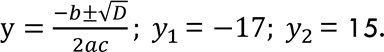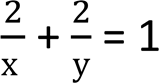"Математичне моделювання. Прикладні задачі. Презентація"
|
Все на світі піддається упорядкуванню та обчисленню… |
МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ.
ПРИКЛАДНІ ЗАДАЧІ
 |
 |
ЗВЕДЕННЯ ДО МАТЕМАТИЧНИХ ТВЕРДЖЕНЬ
МАТЕМАТИЧНА МОДЕЛЬ – ЦЕ ОПИС
ДЕЯКОГО РЕАЛЬНОГО ПРОЦЕСУ ЗАСОБАМИ
МАТЕМАТИКИ
Математичне моделювання – складання математичної моделі задачі
ЕТАПИ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ:
1. побудова математичної моделі;
2. робота з математичною моделлю;
3. 
складання відповіді до задачі в термінах її сюжету
ЯКІ БУВАЮТЬ ЗАДАЧІ:
Математична задача – це абстрактна задача, не прив’язана до жодної життєвої ситуації.
Наприклад:
vЗнайти площу прямокутника зі сторонами 9 см та 12 см.
vСума чисел дорівнює 25. Одне з чисел на 7 менше за інше. Знайти ці числа.
Прикладна задача – це задача, сюжет якої не пов’язаний з математикою.
Наприклад:
vЯка довжина паркану навколо ділянки землі прямокутної форми, що має розміри 12,5м Х 6,8м ? Яка площа цієї ділянки?
v
Два потяги виїхали одночасно назустріч один одному з Харкова та Києва і зустрілись через 5 годин. Яка відстань між містами, якщо швидкість першого потяга 54 км/год, а швидкість другого – 62 км/год?
МАТЕМАТИЧНА ЗАДАЧА № 1
|
|
МОДЕЛЬ - СИСТЕМА |
|
Сума двох чисел дорівнює 8, а їхній добуток 15. Знайти ці числа. Розв'язання 1 етап – побудова математичної моделі х та у – шукані числа. За умовою х + у = 8; ху = 15. Маємо систему: х + у = 8; ቊ ху = 15. 2 етап – робота з математичною моделлю Розв'яжемо систему способом підстановки: х + у = 8; у = 8 − х (1) Підставимо замість у його значення у друге рівняння: х Розв'яжемо друге рівняння: 8х − х2 = 15; −𝑥2 + 8х − 15 = 0 | • (− 1); 𝑥2 − 8𝑥 + 15 = 0. За теоремою, оберненою до теореми Вієта маємо: х1 + х2 = 8; х1х2 = 15. |
|
|
|
|
ПРИКЛАДНА ЗАДАЧА № 1. МОДЕЛЬ – РІВНЯННЯ…
|
Оберіть математичну модель задачі: На двох стоянках 82 автомобілі, причому на першій на шість автомобілів менше, ніж на другій. Скільки автомобілів на кожній стоянці? А. х+ В. Х – (82 – х) = 6 Г. (у – 6) + у = 82. |
ПРИКЛАДНА ЗАДАЧА № 2 МОДЕЛЬ - СИСТЕМА
У яблуневому саду на прямокутній ділянці землі посадили нові дерева, причому кількість рядів на 2 більша, ніж кількість дерев у кожному ряді. Скільки рядів у новому саду і скільки дерев посаджено у кожному ряді, якщо всього посадили 255 дерев?
РОЗВ'ЯЗАННЯ:
|
І ЕТАП: Побудуємо математичну модель ситуації у вигляді системи рівнянь. Введемо змінні х та у. Нехай посадили х рядів по у яблунь у кожному ряді. За умовою х>y на 2. Маємо І рівняння: х – у = 2. Відомо, що посадили 255 яблунь. Маємо ІІ рівняння: ху = 255. х − у = 2 Отримали систему рівнянь: ቊ ху = 255 |
|
х − у = 2, Розв’язуємо систему рівнянь: ቊ ху = 255. У І рівнянні виразимо змінну х через змінну у : х = у + 2. Підставимо вираз у + 2 замість х у друге рівняння системи:
Розв’яжемо ІІ рівняння: у2 + 2у − 255 = 0. a = 1, b = 2, 𝑐 = −255. 𝐷 = 𝑏2 − 4ac = 22 + 4•255 = 1024.
|
ІІ ЕТАП
ПРИКЛАДНА 3АДАЧА № 3.
МОДЕЛЬ – СИСТЕМА
(ЗАДАЧА НА СПІЛЬНУ РОБОТУ)
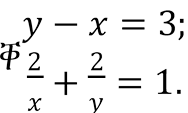
Через дві труби басейн можна наповнити за 2 години. Через першу трубу цей басейн може наповнитися на 3 години швидше, ніж через другу. За скільки годин може наповнитись цей басейн через кожну трубу окремо?
ДО РОЗВ'ЯЗАННЯ ЗАДАЧІ:
Побудова математичної моделі.
Х год – час наповнення басейну через І трубу.
У год – час наповнення басейну через ІІ трубу.
За умовою х < y на 3. Маємо І рівняння: у – х = 3.
|
труби |
p |
t |
A |
|
перша |
1
𝑥 |
2 |
2/x 1 = ቐ + 2/y |
|
друга |
1
𝑦 |
2 |
|
Одержали систему рівнянь – математичну модель задачі:
|
Підсумок уроку:
§ Що таке моделювання?
§ Що таке математичне моделювання?
§ Назвати етапи математичного моделювання.
§ Назвати приклади математичних моделей.
§ Чим відрізняються прикладні задачі від математичних?
|
|
|
-
Дякую!!! -
Дякую за логічність і простоту викладу.
про публікацію авторської розробки
Додати розробку