Головоломки з математики для учнів 6-9 класів
Курйози, загадки, головоломки. Їх роль – це корисний відпочинок. Розв'язуючи їх, можна тренувати свої здібності логічного мислення, не гірше, ніж при розв'язуванні задач, що потребують складання рівнянь.
Головоломки, загадки
Новорічна головоломка
Чотири друга Едуард, Федір, Юрій і Костянтин разом зі своїми дружинами пішли на Новорічне свято. Спочатку кожен танцював зі своєю дружиною. Але потім пари перемішалися. Варя танцювала з Едуардом, Аліна з чоловіком Ольги, Таня з чоловіком Аліни, Федір з жінкою Юри, а Юра з жінкою Едуарда. Спробуйте визначити хто з ким одружений і хто з ким танцював.
Розв’язок
Перш за все, впорядкуємо те, що нам відомо з умови задачі:
- Варя танцювала з Едуардом;
- Аліна танцювала з чоловіком Ольги;
- Таня танцювала з чоловіком Аліни;
- Федір танцював з дружиною Юрія;
- Юрій танцював з дружиною Едуарда.
Перш за все, встановимо, хто дружина Едуарда: це не Варя (див.1 і 5); це не Аліна (див.1 і 3); це не Ольга (див. 1 і 2), отже це Таня. Тепер и знаємо, що Юрій танцював з Танею (див. 5), але за (3) Таня танцювала з чоловіком Аліни. Отже Юра чоловік Аліни. Потім з (4) випливає, що Федір танцював з Аліною, але Аліна (2) танцювала з чоловіком Ольги. Отже, Федір чоловік Ольги. Таким чином, в нас залишилась одна пара Варя і Костя.
13 маленьких питань
- Як отримати 50, відняв від 40 десять?
- Які натуральні числа, що записані за допомогою двох цифр, збільшуються при видаленні одної цифри, що стоїть ліворуч?
- Що за дріб, у якого чисельник менше за знаменник і який не зміниться, якщо його записати вверх ногами.
- Як зменшити число 989 на 303, нічого з нього не віднімаючи?
- В одній родині п’ятеро братів. Кожен з них має сестру. Скільки дітей в цій родині?
- Одного разу Іванова запитали, хто зображений на портреті, що на стінці.
Іванов відповів:
- Батько, зображеного на портреті обличчя, є
єдиним сином того, хто це каже. Чий це портрет?
- Число 12 можна розділити на 2, 3, 4, 6 частин. На скільки частин необхідно розділити 12, аби добуток цих частин був найбільшим.
- 1 кг яблук, 1 кг слив і 1 кг помідорів коштують разом 4 грн; 2 кг яблук, 1 кг слив і 1 кг помідорів коштують 4 грн 80 коп; 1 кг яблук, 2 кг слив і 1 кг помідор коштують 5 грн 20 коп. скільки коштують 1 кг яблук, скільки 1 кг слив, а скільки 1 кг помідорів?
- Напишіть число, яке складається з 22 тисяч, 22 сотні і 22 одиниці.
- Різниця двох додатних чисел 1, а їх сума 6. Назвіть ці числа.
- Добуток трьох послідовних натуральних чисел дорівнює 120, добуток крайніх чисел дорівнює 24. Вкажіть ці числа.
- Коли сину виповнилося 6 років. його батькові було 30 років. Зараз батько в чотири рази старший від сина. Скільки років сину?
- Яке найбільше число можна написати за допомогою чотирьох одиниць?
Відповіді
- XL=40, якщо тепер видалимо X від XL, то залишиться L=50.
- Якщо римське число XIII розріжемо навпіл горизонтальною рискою, то отримаємо VIII , тобто 8.
-
Дріб
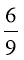 , повернувши його «вверх ногами» знову отримаємо
, повернувши його «вверх ногами» знову отримаємо 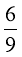 .
.
- Число 989 потрібно повернути на 180°, отримаємо 686, а 989–686=303.
- Шестеро.
- Це був портрет внука Іванова.
- На чотири частини, оскільки найбільшим добутком буде 3·3·3·3=81.
- 1 кг яблук коштує 80 коп., слив – 1 грн 20 коп., помідорів 2 грн.
- 24 222.
- Це пара чисел 3,5 і 2,5.
- Це числа 4; 5; 6.
- 8 років сину, 32 роки батькові.
-
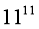 Це число, яке має 12 знаків. Але 1111! (факторіал) – більше!
Це число, яке має 12 знаків. Але 1111! (факторіал) – більше!
Запишіть
- Запишіть найбільше число трьома цифрами.
- Виразіть 1000 за допомогою:
а) п’яти або дев’яти дев’яток,
б) шести тройок,
в) тринадцяти п’ятірок,
г) всіх десяти цифр.
3. Виразіть 1 за допомогою:
а) цифр 1, 2, 3;
б) всіх десяти цифр.
4. Виразіть 100, використовуючи для цього п’ять одиниць, п’ять трійок і п’ять шісток.
Розв’язок
-
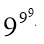 ;
;
-
а)
 ;
; 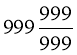 ;
;
б) 333·3+![]() ;
;
в) 5·5·5·5+5·5·5+5·5·5+5·5·5;
г) 90·5·4:2+87+16–3.
-
а)
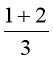 ,
, 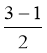 ,
, 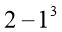 ;
;
б) ![]() або
або 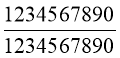 ;
;
4. 111–11=33·3+![]() =5·5·5–5·5.
=5·5·5–5·5.
Які арифметичні дії?
Між цифрами поставте знаки таких арифметичних дій. Щоб рівності були вірними.
а) 12=2; д) 123456=2;
б) 123=2; е) 1234567=2;
в) 1234=2; ж) 12345678=2;
г) 12345=2; з) 123456789=2.
Розв’язок
а) 1·2=2; д) (1+2)·3+4–5–6=2;
б) 1–2+3=2; е) 1·2·3+4+5–6–7=2;
в) 1·2·3–4=24 ж) (1+23):4+5+6–7–8=2;
г) (1·2·3+4):5=2; з) 1+2–3+4·5+6–7–8–9=
Розшифруй
Польське експортне підприємство, що займається експортом деревини, відправило своєму представнику в Лондон зашифровану телеграму наступного складу « маємо на складі Гора-Лєр кубічних метрів соснових дощок , Гера кубічних метрів дубових дощок, Лаба-роба листків ольхової фанери. Ціни не понижати. За бажанням можемо доставити Ірен куб.метрів дубової стружки » . Представник мав , звичайно ключ для розшифрування цієї телеграми. Пропонуємо вам знайти цей ключ за допомогою наступних вказівок:
- Ключ математичний термін з 9 літер.
- Кожна буква цього слова позначає цифру
- Необхідно замінити кожну літеру цього слова послідовним рядом цифр від 1 до 9
- Ключ потрібно скласти з перших літер слів, значення яких зазначені нижче:
- Наука про фігури, взаємне їх розташування і розміри їх части та елементів.
- Дванадцятигранник.
- Математичний знак для позначення дії додавання.
- Древньогрецький математик, автор «начал».
- Одне з понять комбінаторики.
- Видатний математик 17 століття, один з основоположників теорії ймовірності, розв’язав задачу про брахистохрону
- Крива в площині Лобачевского що є геометричним місцем кінців січних однакового нахилу , проведених з деякої точки А прямої а до прямих, що паралельні її в визначеному напрямку і лежать з нею в одній площині.
- Видатний Російський математик, основоположник неевклідової геометрії.
- Дошка для рахування у древніх греків та римлян.
Вказати повний текст телеграми.
Розв’язок
1) Геометрія; 2) Ікосаедр; 3) Плюс;
4) Евклід; 5) Розміщення; 6) Бернуллі; 7) Орицикл ; 8) Лобачевский; 9) Акаба.
З перших літер цих слів складається слово «ГІПЕРБОЛА». Тепер згідно ключа, маємо наступні значення літер Г=1, І=2, П=3, Е=4, Р=5, Б=6, О=7, Л=8, А=9. Залишається тільки вставити в телеграму замість літер ці цифри, аби повністю її розшифрувати.
Чотиризначна головоломка
Визначте число:
- Воно чотиризначне;
- Перша цифра вдвічі більша від другої;
- Сума першої і другої цифр дорівнює третій;
- Якщо додамо всі чотири цифри, то отримаємо число, в якому перша цифра дорівнює різниці четвертої і третьої, а її добуток на другу цифру заданого числа, дорівнює першій цифрі заданого числа.
Розв’язок
Нехай нашими цифрами будуть a, b, c, d.
Тоді a=2b; c=a+b=3b.
Оскільки кожна цифра менша або дорівнює 9, то цифрою b може бути 1, 2 або 3.
Нехай першою цифрою суми a+b+c+d буде a1. Тоді a1b=a, тобто a1b=2b , з цього a1=2. Тепер a1=d–c=d–3b. Підставимо 2 замість a1 і послідовно 1, 2 і 3 – замість b знайдемо послідовно три значення для d: d=5, d=8, d=11 (не підходить)
Після перевірки отримаємо a=4, b=2, c=6, d=8 . Шукане число 4268.
Відповідь: 4268.
Гра з цифрами
1)З дев’яти цифр 1, 2, 3, …, 9 скласти такі числа, аби їх сума дорівнювала 100. Цифри, що утворюють кожну складену вами суму, повинні зустрічатися в ній лише один раз і розташовуватись в натуральній послідовності. Між числами можна ставити знаки плюс і мінус. Перед першим числом мінус стояти не може.
2) виконати те саме завдання, але за умови, що цифри повинні розташовуватися в зворотній послідовності, тобто від 9 до 1.
Розв’язок
1)
123–45–67+89=100;
123+4–5+67–89=100;
123+45–67+8–9=100;
123–4–5–6–7+8–9=100;
12–3–4+5–6+7+89=100;
1+23–4+5+6+78–9=100;
1+2+34–5+67–8+9=100;
12+3–4+5+67+8+9=100;
1+23–4+56+7+8+9=100;
1+2+3–4+5+6+78+9=100.
2)
98–76+54+3+21=100;
98+76+54–32+1=100;
98–7–6–5–4+3+21=100;
9–8+7+65–4+32–1=100;
9–8+76–5+4+3+21=100;
98–7+6+5+4–3–2–1=100;
98+7–6+5–4+3–2–1=100;
98+7+6–5–4–3+2–1=100;
98+7–6+5–4–3+2+1=100;
98–7+6+5–4+3–2+1=100;
98–7+6–5+4+3+2–1=100;
98+7–6–5+4+3–2+1=100;
98–7–6+5+4+3+2+1=100;
9+8+76+5+4–3+2–1=100;
9+8+76+5–4+3+2+1=100.
Скільки сторінок?
Для того, аби пронумерувати сторінки одного роману використали 3389 цифр. Скільки сторінок в цій книзі?
Розв’язок
Для того аби пронумерувати сторінки від 1 до 9, необхідно 1·9=9 цифр. Для того, щоб пронумерувати сторінки від 10 до 99, необхідно
2·90=180 цифр.
Для того, щоб пронумерувати сторінки від 100 до 999, необхідно 3·900=2700 цифр. Отже, щоб пронумерувати сторінки від 1 до 999 необхідно 9+180+2700=2889 цифр. Залишок 3389–2889=500 цифр використали для нумерації наступних сторінок, починаючи зі сторінки 1000. Цих сторінок було 500:4=125. Тобто, всього в книзі 999+125=1124 сторінки.
Відповідь: 1124
Без кохання
Чотири юнака : Андрій, Борис, Кирило та Дмитро закохані (без взаємності) в чотирьох дівчат: Таню, Машу, Зіну та Галю, які теж закохані без взаємності. Андрій кохає дівчину, закохану в юнака, який кохає Таню. В Машу закоханий юнак, якого кохає дівчина, яку кохає Борис. Кирило закоханий в дівчину, яка кохає Дмитра. Якщо Бориса не любить Зіна, і юнак, якого кохає Галя не кохає Зіна, то кого кохає Андрій?
Розв’язок.
Нехай символ х → у позначає, що х кохає у, а символ х ← у - х не кохає у.
Отже маємо:
І. А → ?→ ?→ Т → ?
ІІ. Б → ? → ? → М → ?
ІІІ. К → ? → Д
ІV. З ← Б
V. Г → ? ← З
Умова, що без взаємного кохання неможна очікувати взаємності, дозволяє нам передбачити , що маємо справу з замкнутим колом, що складається з 8 людей, або з двома замкнутими колами, що складаються з 4 людей. Нехай вірне друге міркування . З цього випливає, що оскільки К і Д належать одному колу (умова ІІІ), то А і Б також повинні належати до того ж кола. Тепер А → М → Б → Т → А. але оскільки З і Г також належать до цього ж кола то стає неможлива умова V. З цього випливає, що всі вісім чоловік належать одному колу.
Тепер ми можемо сказати, що Таню не кохає Андрій (умова І), і не Дмитро (умова ІІІ), і не Кирило, що б суперечило умові V. Отже, Таню кохає Борис.
Далі, Андрій любить Галю, Галя любить Бориса, Борис любить Таню, Таня кохає Кирила, Кирило любить Машу, Маша кохає Дмитра, Дмитро кохає Зіну, Зіна любить Андрія.
В залі
В залі клубу 320 місць, розміщених рядами. Після того, як число місць у кожному ряду збільшили на 4 і додали ще один такий ряд, в залі стало 420 місць. Скільки стало рядів в залі?
Розв’язок
Нехай в залі х рядів по у місць у кожному. Тоді ху=320. Після збільшення місць в ряду їх стало у+4, а рядів х+1. отже, (х+1)(у+4)=420. маємо систему:

![]()
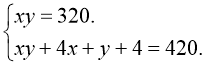
Її розв’язки 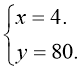 та
та 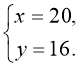
За змістом задачі в залі став 21 ряд (бо залів, в яких 4 ряди по 80 місць в кожному практично не буває).
Відповідь: 21 ряд.
Логічна головоломка
- Прізвище машиніста поїзда, помічника машиніста та кондуктора – але не в тій послідовності – Ковальов, Петров, Смірнов;
- Прізвище пасажирів: лікар Ковальов, лікар Петров, лікар Смірнов.
- Лікар Ковальов живе в Москві;
- Кондуктор живе посередині шляху від Москви до Санкт-Петербурга;
- Пасажир, що має теж прізвище, що і кондуктор, живе в Санкт-Петербурзі;
- Лікар Петров заробляє щомісяця 10000 рублів;
- Пасажир, що живе дуже близько біля кондуктора, заробляє рівно втричі більше, ніж кондуктор;
- Смірнов виграв партію шахів в помічника машиніста. Яке прізвище машиніста?
Розв’язок
Три пасажира живуть в різних містах. Лікар Петров – це не той, хто заробляє втричі більше від кондуктора, оскільки його заробітна плата не ділиться рівно на три, саме в цій умові є ключ до розв’язку задачі. Лікар Петров також не той, хто живе в Москві, отже Петров це пасажир, який живе в Санкт-Петербурзі. А з цього випливає, що прізвище кондуктора Петров. Тепер прізвище машиніста або Смірнов, або Ковальов. Але нам відомо, що Смірнов виграв у помічника машиніста партію в шахи, отже Смірнов і є машиністом.
Старик Хоттабич
Вік старика Хоттабича записується числом з різними числами. Відомо, якщо першу і останню цифри закреслити, то отримаємо двоцифрове число, сума цифр якого дорівнює 13 і є найбільшою. Перша цифра більша за останню і 4 рази. Скільки років Хоттабичу?
Розв’язок
Найбільше двоцифрове число з сумою цифр 13 є число 94. Нехай остання цифра 1, тоді перша буде 1·4=4 – не задовольняє умову, бо в цьому числі цифри повторюються. Нехай остання цифра 2, тоді 2·4=8. Отже, дане число 8942.
Відповідь: 8942
Скільки років дяді?
- Дядя, скільки тобі років?
- Вдвічі більше ніж тьоті Валі.
- А скільки років тьоті Валі?
- Втричі менше, ніж тьоті Галі.
- А скільки років тьоті Галі?
- Тьотя Галя на 20 років старша Нюри.
- Дядя, а скільки років Нюрі?
- Нюра в п’ять разів старша Ані.
- А скільки років Ані?
- Не набридай. Через рік їй виповниться шість років.
- Дядя, а хочете я скажу, скільки вам років.
А й справді, скільки років дяді?
Розв’язок
Ані 5 років.
Нюрі 5·5=25 років.
Тьоті Галі 25+20=45 років.
Тьоті Валі 45:3=15
Років.
Дяді 15·2=30 років.
Відповідь: 30 років.
Як розділити спадок?
Один римлянин, помираючи, залишив заповіт на користь своєї дружини і дитини, яка мала скоро народитися. Якщо на світ з’явиться хлопчик, то він має отримати дві третини спадку, а дружина одну третину. Якщо ж народиться дівчинка, то вона мала отримати одну третину, а дві третини – мати. Але на світ народилися близнята: хлопчик і дівчинка. Як тепер поділити спадок?
Розв’язок
Римський юрист Сальвій так розв’язав цю задачу: спадок необхідно розділити на 7 частин;
![]() отримує син,
отримує син, ![]() жінка,
жінка, ![]() дочка. При такому розділі буде виконуватися воля батька, аби син отримав вдвічі більше, ніж мати, а дочка – вдвічі менше, ніж мати.
дочка. При такому розділі буде виконуватися воля батька, аби син отримав вдвічі більше, ніж мати, а дочка – вдвічі менше, ніж мати.
Як вона справилась?
В каструлю потрібно налити 4 літра води. У господині є лише два сосуди: один об’ємом 5 літрів, а другий об’ємом 3 літри. Як вчинила господиня?
Розв’язок
Господиня заповнила 5-літрову посудину. З неї перелила 3 літра в 3-літрову і потім ці три літра вилила взагалі. Ті 2 літри, що залишилися в 5-літровому сосуді вона вилила в 3-літровий сосуд. Потім вона знову наповнила 5-літрову каструлю водою і з неї один літр перелила в 3-літрову посудину. В великій каструлі залишилось рівно 5 літрів.
Екзамени
Студент за 5 років навчання склав 31 екзамен. Кожного наступного року він складав більше екзаменів, ніж у попередньому. На п’ятому курсі екзаменів було втричі більше, ніж на першому. Скільки екзаменів було на четвертому курсі?
Розв’язок
Студент не міг мат и на першому курсі два екзамени, тому, що в цьому випадку за п’ять років загальна кількість екзаменів була б менша за 31. чотири екзамени і більше він теж не міг мати на першому курсі. Справді, тоді він мав би не менше ніж 4+5+6+7+12=34 екзамени, тобто більше ніж 31. отже на першому курсі студент мав тільки три екзамени, а на останньому 9. в цьому випадку він міг мати на четвертому курсі тільки 8 екзаменів.
Відповідь: 8 екзаменів.
Скільки років?
Івану, Петру, Семену та їх дружинам Ользі, Ірині і Анні всім разом 151 рік, причому кожен чоловік старший за свою дружину на п’ять років.
Іван на один рік старший від Ірини; Ользі і Івану разом 48 років, а Семену і Ользі разом 52 роки.
Пропоную дізнатися, хто з ким одружений і скільки кожному років.
Розв’язок
Нехай Івану – Х років, Петру –Y і Семену Z років. Тоді вік їх дружин відповідно Х–5, Y–5,
Z – 5.
Іван не може бути чоловіком Ірини, за умови. Отже його дружина або Ольга, або Анна. Якщо міркувати, що вік кожного має бути цілим числом, то Ольга не може бути дружиною Івана, оскільки сума їх років разом (48) не може бути виражена сумою двох цілих чисел, різниця яких 5. тому, дружина Івана Анна, якій було Х–5 років. Розмірковуючи так далі, знайдемо, що Ольга не може бути дружиною Семена, тому вона дружина Петра, її вік (Y–5 років).А Семен відповідно одружений на Ірині (Z - 5)
За умовою задач:
- X+Y+Z+X–5+Y–5+Z–5=151
aбо X+Y+Z=83;
- X+Y–5=48 або X+Y=53;
- Z+Y–5=52 або Z+Y= 57.
Розв’язуючи ці рівняння, знаходимо з 1-го і 3-го, що Z=30, тобто Семену 30 років і Ірині 25. З 2-го рівняння X=26, тобто Івані 26 років і Анні 21 рік; Y=27, тобто Петру 27 років і Ользі 22 роки.
Як написати?
- одиницю трьома п’ятірками;
- нуль трьома п’ятірками;
- два трьома п’ятірками;
- 31 п’ятьома трійками.
Розв’язок
1) 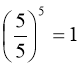 тому, що
тому, що 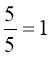 і 15 = 1;
і 15 = 1;
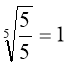 тому, що
тому, що 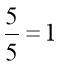 і
і ![]()
- (5-5)5=0 тому, що 5–5=0, а 05=0;
5·(5-5)=0;
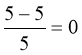
![]()
-
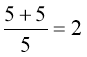 ;
;
-
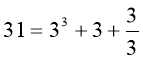 ;
;
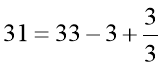 ;
; 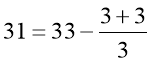 .
.
Прилив
Біля берега стоїть корабель зі мотузковою драбиною, що спущена вздовж борту. У драбини 10 сходинок. Відстань між сходинками 30 см. Найнижча сходинка дотикається поверхні водою океан сьогодні спокійний, але почався прилив, що піднімає воду за кожну годину на 15 см. Через скільки часу покриється водою третя сходинка?
Розв’язок
Вода ніколи не покриє третю сходинку, оскільки разом з водою буде підніматися і корабель і драбина.
У буфеті
У черзі в шкільному буфеті стоять Юра, Коля, Володя, Саша та Олег. Юра стоїть перед Колею, але після Олега. Володя і Олег не стоять поруч, а Саша не знаходиться поруч ні з Олегом, ні з Володею. В якому порядку стоять хлопчики? Розв’язок
Якби Саша стояв всередині черги, він був би поряд з двома якими-небудь хлопчиками. Але за умовою відомо, що він не стоїть поряд ні з Юрою, ні з Володею, ні з Олегом, а хлопчиків всього п’ять. Отже, Саша стоїть або на початку або в кінці черги, а поряд з ним (другим або четвертим) стоїть Коля. Але відомо, що Юра стоїть перед Колею, отже Коля не стоїть другим (тоді перед ним стояв би тільки Саша) і, отже, стоїть четвертим (а Саша п’ятим). Якби Юра стояв перед Колею, то першим і другим стояли б Володя і Олег. Але відомо, що вони поряд не стоять. Отже, Юра стоїть другим, Олег першим, а Володя – третім.
Відповідь: хлопчики стоять в такому порядку: Олег, Юра, Володя, Коля, Саша.
Годинники
Як можна відміряти 9 хвилин за допомогою пісочних годинників на 5 хвилин та на 7 хвилин?
Розв’язок
Встановлюємо обидва годинника і , коли пройде 5 хвилин, перевертаємо п’ятихвилинний годинник, а потім, коли закінчить йти семихвилинний годинник, п’ятихвилинний потрібно перевернути знову, і чекати поки він знову зупиниться. Таким чином відмірюється 9 хвилин.
Коробки
У мене в трьох коробках лежать цвяхи, гвинти і гайки. На кришці кожної коробки було написано, що в ній лежить. Одного разу мій молодший братик переставив кришки коробок так, що надписи на них перестали відповідати вмістові коробок. Чи можна, відкривши одну з коробок, визначити, що лежить в кожній коробці?
Розв’язок
Нехай ми відкрили коробку з надписом «Гвинти», а в ній виявились цвяхи, отже, в тій коробці, на якій надпис «Гайки», будуть гвинти, а в тій, на якій надпис «Цвяхи», будуть гайки, тому що за умовою відомо, що надписи на коробках перестали відповідати вмістові коробок. Отже, можна, відкривши одну з коробок, визначити, що лежить в кожній коробці.
Відповідь: так.
Закресліть
У числі 12345123451234512345 закресліть 10 цифр так, щоб залишилося найбільше можливе число.
Відповідь: 5534512345.


про публікацію авторської розробки
Додати розробку
