Підсумкові контрольні роботи, математика 9 клас
Про матеріал
Дані завдання розироблені для проведення ДПА з математики в 9 класі. Зміст усіх завдань відповідає чинній програмі - «Навчальна програма з математики для 5-9-х класів для загальноосвітніх навчальних закладів затверджена наказом МОН від 07.06.2017 № 804».
Перегляд файлу
Підсумкові контрольні роботи з математики 9 клас
2017-2018 навчальний рік
Підготувала
вчитель математики та інформатики
Тарасівської загальноосвітньої школи І-ІІІ ступенів
Зіньківської районної ради
Полтавської області
Пояснювальна записка
Зміст усіх завдань відповідає чинній програмі - «Навчальна програма з математики для 5-9-х класів для загальноосвітніх навчальних закладів затверджена наказом МОН від 07.06.2017 № 804».
Для виконання підсумкової контрольної роботи з математики для учнів загальноосвітніх навчальних закладів рекомендовано відвести 135 хвилин, час який учні використають підчас підписання бланку відповідей не враховується у вище зазначений.
Перша частина підсумкової контрольної роботи містить 12 тестових завдань завдань закритого типу (8 завдань з алгебри і 4 з геометрії) з можливістю вибору однієї правильної відповіді з чотирьох запропонованих. Якщо учень указав у бланку правильну відповідь то йому нараховують 2 бали, якщо вказана неправильна відповідь – 0 балів. Максимальна кількість балів за розв’язання завдань першої частини – 24.
Друга частина підсумкової контрольної роботи містить 4 тестові завдання відкритого типу(3 завдання з алгебри й 1 завдання з геометрії) із записом короткої відповіді. Завдання цієї частини вважаються розв’язаними правильно, якщо учень у бланку записав коротку відповідь у вигляді виразу, числа, координат точки, розв’язків рівнянь тощо. Якщо учень записав у бланку правильну відповідь, то йому нараховують 3 бали, у випадку неповної відповіді на розсуд учителя (наприклад, указано один із коренів рівняння тощо) він може одержати 1 чи 2 бали, неправильна відповідь – 0 балів. Максимальна кількість балів за розв’язання завдань другої частини 12.
Третя частина підсумкової контрольної роботи містить 3 завдання відкритого типу (2 завдання з алгебри й 1 завдання з геометрії) із записом повної відповіді. Завдання вважатиметься розв’язаним правильно, якщо учень виконав обґрунтування кожного кроку розв’язання і записав правильну відповідь. За розв’язання кожного завдання цієї частини учневі нараховують від 4 до 0 балів. Максимальна кількість балів за розв’язання завдань третьої частини – 12.
Максимальна кількість балів, яку може отримати учень – 48. Для виставлення оцінки за виконання підсумкової контрольної роботи у 12-бальній шкалі оцінювання набрану учнем кількість балів слід поділити на 4.
Бланк відповідей
державної підсумкової атестації з математики
учня (учениці) 9 ____ класу
____________________________________
____________________________________
назва навчально закладу
__________________________________
прізвище, ім’я, по батькові учня (учениці)
Варіант № ________
Увага! Відмічайте один варіант відповіді до кожного завдання. Якщо потрібно змінити відповідь у деяких завданнях, то правильну відповідь зазначте у відведеному місці
У завданнях 1.1 – 1.12 правильну відповідь позначайте так: 
А Б В Г



 1.1.
1.1.




 1.2.
1.2.






 1.3.
1.3.
1.4.
А Б В Г



 1.5.
1.5.




 1.6.
1.6.






 1.7.
1.7.
1.8.
А Б В Г



 1.9.
1.9.




 1.10.
1.10.






 1.11.
1.11.
1.12.
У завданнях 2.1 – 2.4 запишіть правильну відповідь:
2.1._______________________
2.2._______________________
2.3._______________________
2.4._______________________
Для виправлень
Завдання 1.1 – 1.12
номер
завдання А Б В Г



 1.
1. 





 1.
1. 







 1.
1. 

1. 

Завдання 2.1 – 2.4
номер
завдання
2.  ____________________
____________________
2.  _____________________
_____________________
ВАРІАНТ №1
Частина перша
У завданнях 1.1 – 1.12 серед чотирьох варіантів відповідей виберіть один ПРАВИЛЬНИЙ і позначте його у бланку відповідей.
1.1. Укажіть число, яке ділиться на 5 і на 9.
А 8253 Б 2585 В 2358 Г 2835
1.2. Коренем якого рівняння є число 6?
А х – 13=30 Б 6 ∙ х = 56 В 49 : х=7 Г 25 – х = 19
1.3. Знайдіть значення функції у=2х – 3 у точці 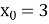 .
.
А – 9 Б 9 В 3 Г – 3
1.4. Спростіть вираз  .
.
А  Б
Б 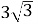 В
В 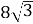 Г
Г 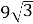
1.5. Вкажіть вираз, який не набуває додатних значень.
А 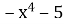 Б
Б 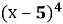 В
В 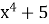 Г
Г 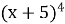
1.6. Чому дорівнює добуток коренів квадратного рівняння 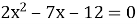 ?
?
А 12 Б –12 В –7 Г –6
1.7. Кутовий коефіцієнт якої з наведених прямих дорівнює 5?
А 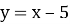
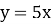
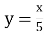 Г
Г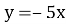
1.8. Чому дорівнює середнє значення вибірки 4, 5, 6, 7, 8, 8, 9, 12, 13?
А 7 Б 8 В 9 Г 11
1.9. Знайдіть уписаний у коло кут, якщо він спирається на дугу, яка становить  кола.
кола.
А 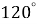 Б
Б 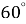 В
В 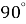 Г
Г 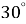
1.10. Сторони прямокутника дорівнюють 32 см і 24 см. Знайдіть довжину діагоналі прямокутника.
А 40 см Б 80 см В  см Г
см Г 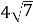 см
см
1.11. Дві сторони трикутника дорівнюють 3 см і 4 см, а кут між ними - 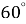 . Знайдіть невідому сторону трикутника.
. Знайдіть невідому сторону трикутника.
А 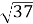 см Б
см Б  см В
см В 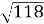 см Г
см Г 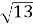 см
см
1.12. Які координати має образ точки А (–2; 5) при симетрії відносно початку координат?
А (2; 5) Б (2; –5) В (–2; –5) Г (5; –2)
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Відповідь запишіть у бланк відповідей.
2.1. Яку суму грошей слід поставити в банк під 10% річних, щоб через 2 роки на рахунку стало 4840 грн?
2.2. Перетворіть вираз 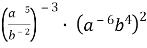 так, щоб він не містив степенів з від’ємним показником.
так, щоб він не містив степенів з від’ємним показником.
2.3. На чотирьох карточках записано числа 3, 6, 7 і 10. Яка ймовірність того, що добуток чисел, записаних на двох навмання вибраних картках, буде кратним числу 14.
2.4. Обчисліть площу ромба, одна з діагоналей якого дорівнює 12 см, а сторона – 10 см.
Частина третя
Розв’яжіть завдання 3.1 – 3.3, запишіть повне обґрунтування.
3.1. Для класу закупили 30 ручок і 25 олівців, заплативши за все 140 грн. Скільки коштує ручка і скільки – олівець, якщо 10 ручок коштують стільки ж, скільки 15 олівців?
3.2. Знайдіть суму всіх від’ємних членів арифметичної прогресії –3,8; –3,5; –3,2; –2,9… .
3.3. Доведіть, що чотирикутник ABCD з вершинами у точках А(2; 1), В(1; –3), С(–3; –2), D(–2; 2) є прямокутнкиком.
ВАРІАНТ №2
Частина перша
У завданнях 1.1 – 1.12 серед чотирьох варіантів відповідей виберіть один ПРАВИЛЬНИЙ і позначте його у бланку відповідей.
1.1. Обчисліть значення виразу (1602–102) : 50.
А 300 Б 75000 В 30 Г 7500
1.2. Яку частину хвилини становить 23 с?
А 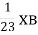 Б
Б 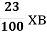 В
В  Г
Г 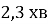
1.3. Якому одночлену дорівнює вираз 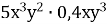 ?
?
А 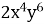 Б
Б 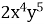 В
В 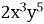 Г
Г 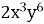
1.4. Скоротіть дріб 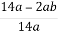 .
.
А 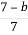 Б
Б 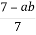 В
В 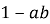
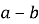
1.5. Функцію задано формулою 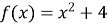 . Знайдіть
. Знайдіть 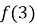
А 4 Б –13 В 13 Г –5
1.6. Вершини якої з парабол належать осі ординат?
А 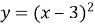 Б
Б  В
В 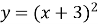 Г
Г 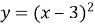 +1
+1
1.7. Розв’яжіть рівняння 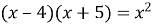 .
.
А –20 Б 4; 5 В 20 Г –4;
1.8. Дано вибірку 1, 2, 3, 4, 5, 7, 7, 8, 9. Знайдіть медіану цієї вибірки.
А 2 Б 4 В 7 Г 5
1.9. Знайдіть найменший з кутів чотирикутника, якщо величини його кутів пропорційні числам 2, 5, 6 і 7.
А 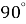 Б
Б 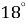 В
В 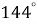 Г
Г 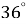
1.10. Катети прямокутного трикутника дорівнюють 2 см і 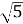 см. Знайдіть косинус меншого гострого кута цього трикутника.
см. Знайдіть косинус меншого гострого кута цього трикутника.
А 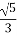 Б
Б 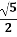 В
В  Г
Г 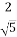
1.11. Знайдіть координати вектора 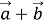 , якщо
, якщо 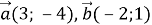 .
.
А А(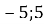
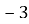
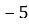
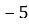
1.12. Точка С – середина відрізка АВ. Знайдіть координати точки В, якщо А(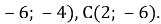
А А(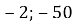
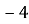
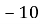
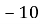

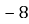
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Відповідь запишіть у бланк відповідей.
2.1. Щоб ліквідувати запізнення на 24 хв, потяг на перегоні завдовжки 120 км збільшив швидкість на 10 км/год порівняно із запланованою. З якою швидкістю мав їхати потяг?
2.2. Скільки цілих чисел містить множина розв’язків нерівності 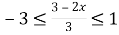 .
.
2.3. Скоротіть дріб  .
.
2.4. Відрізок МК – середня лінія трикутника ABC (MK||BC). Площа трикутника AMK дорівнює 36  . Чому дорівнює площа чотирикутника BMKC?
. Чому дорівнює площа чотирикутника BMKC?
Частина третя
Розв’яжіть завдання 3.1 – 3.3, запишіть повне обґрунтування.
3.1. Розв’яжіть систему рівнянь 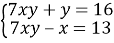 .
.
3.2. Знайдіть область визначення функції 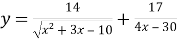 .
.
3.3. Бічна сторона рівнобедреного трикутника точкою дотику вписаного кола ділиться у співвідношенні 8 : 9, рахуючи від вершини кута при основі трикутника. Знайдіть периметр трикутника, якщо радіус вписаного кола дорівнює 16 см.
ВАРІАНТ №3
Частина перша
У завданнях 1.1 – 1.12 серед чотирьох варіантів відповідей виберіть один ПРАВИЛЬНИЙ і позначте його у бланку відповідей.
1.1. Якщо задумане число помножити на 3 і до одержаного результату додати 5, то матимемо 56. Яке число задумали?
А 183 Б 17 В 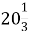 Г 7
Г 7
1.2. Довжина автомобільної траси становить 360 км. Знайдіть довжину цієї траси на карті з масштабом 1:10 000 000.
А 36 см Б 9 см В 3,6 см Г 90 см
1.3. Обчисліть значення виразу 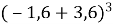 .
.
А 8 Б 16 В 4 Г 3
1.4. Спростіть вираз 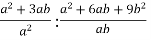 .
.
А 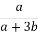 Б
Б 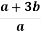 В
В 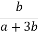 Г
Г 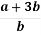
1.5. Обчисліть значення виразу 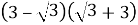 .
.
А 6 Б 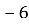
1.6. Знайдіть дискримінант квадратного рівняння 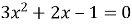 .
.
А 1 Б 16 В 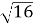 Г 3
Г 3
1.7. Яка з нерівностей є хибною при всіх значеннях x.
А 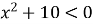 Б
Б 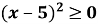 В
В 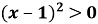 Г
Г 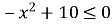
1.8. У коробці є 42 картки, пронумеровані числами від 1 до 42. Яка ймовірність того, що номер навмання взятої картки не буде кратним числу 7?
А  Б
Б  В
В  Г
Г 
1.9. Один з кутів ромба дорівнює 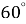 . Знайдіть меншу діагональ ромба, якщо його сторона дорівнює 15 см.
. Знайдіть меншу діагональ ромба, якщо його сторона дорівнює 15 см.
А 15 см Б 7,5 см В 10 см Г 30 см
1.10. Знайдіть вписаний кут, який спирається на дугу, що становить  кола.
кола.
А 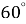 Б
Б  В
В 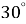 Г
Г 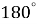
1.11. Знайдіть зовнішній кут при вершині правильного шестикутника.
А 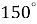 Б
Б 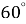 В
В 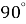 Г
Г 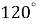
1.12. Знайдіть координати вектора 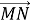 , якщо
, якщо 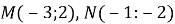 .
.
А (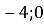

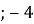
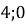
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Відповідь запишіть у бланк відповідей.
2.1. Знайдіть координати точок перетину прямої 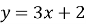
2.2. Чому дорівнює сума десяти перших членів арифметичної прогресії 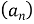 , якщо
, якщо 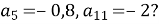
2.3. Підкидають дві монети. Яка ймовірність, що випаде два герби?
2.4. Один з катетів прямокутного трикутника дорівнює 15 см, а медіана, проведена до гіпотенузи, 8,5 см. Обчисліть площу даного трикутника.
Частина третя
Розв’яжіть завдання 3.1 – 3.3, запишіть повне обґрунтування.
3.1. Два оператори комп'ютерного набору, працюючи разом, набрали рукопис посібника за 12 год. За скільки годин може виконати це завдання кожен оператор, працюючи самостійно, якщо один з них може це зробити на год швидше від іншого?
3.2. Відомо, що 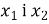 – корені рівняння
– корені рівняння 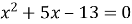 . Не розв'язуючи цього рівняння, знайдіть значення виразу
. Не розв'язуючи цього рівняння, знайдіть значення виразу 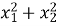 .
.
3.3. Основи рівнобічної трапеції дорівнює 5 см і 13 см, а діагональ ділить її гострий її гострий кут навпіл. Знайдіть площу трапеції.
docx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
