Презентація "У кого бджоли - у того й мед" (заняття математичного гуртка для учнів 8-9 класів)

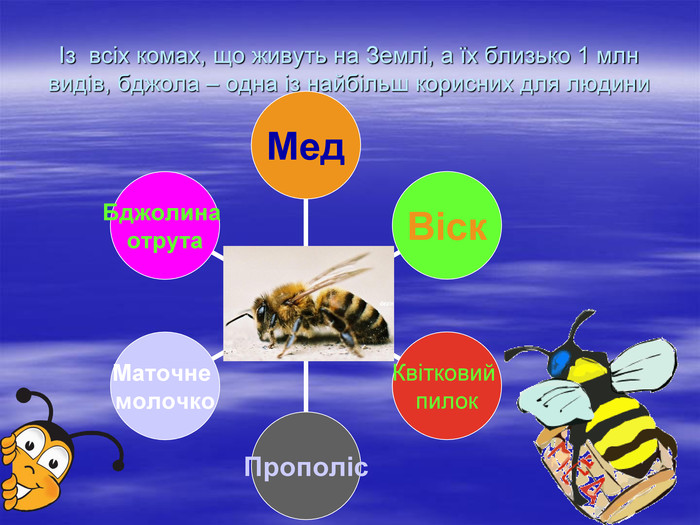
КЗ «БЛАГОДАТНЕНСЬКА ЗШ І-ІІІ СТУПЕНІВ» БОБРИНЕЦЬКОЇ РАЙОННОЇ РАДИ КІРОВОГРАДСЬКОЇ ОБЛАСТІ ВЧИТЕЛЬ КОРОВІНА НАДІЯ ІВАНІВНА Заняття математичного гуртка «Піфагорчики»

Мета заняття опанування змісту математичних законів шляхом спостереження за проявами закономірностей в навколишньому середовищі, що сприяє усвідомленню практичного застосування набутих теоретичних знань.

Мёд есть сок с росы небесной, который пчёлы собирают во время доброе с цветов благоуханных, и от того имеет в себе силу многу и угоден бывает к лекарству от многих болезней» (із старовинного рукописного російського травника)

В стародавній Греції і Римі мед вважали подарунком неба, їжою богів. Бджіл, як священних тварин, зображали на скалах, монетах, викарбовували на гробницях, пірамідах.

В Єгипті медоносна бджола – символ вірності, хоробрості і зневаги до смерті. Адже бджоли, захищаючи свій дім, ніколи не відступають перед небезпекою і не втікають

Із всіх комах, що живуть на Землі, а їх близько 1 млн видів, бджола – одна із найбільш корисних для людини Бджолина отрута Маточне молочко Прополіс Квітковий пилок Віск Мед

Люди Охорона Бджоли Довкілля

1. Можливо вибір бджо-лами такої форми сот зумовлений більшою вмісткістю порівняно з сотами іншої форми. 2. Або ж це зв’язано з економією воску, необ-хідного для створення комірок сот

Серед багатьох ін-стинктивних про-явів, властивих дивним створінням – бджолам, найбіль-ше захоплення ви-кликає створення ними ідеальних за формою сот

Правильні многокутники зустрічаються в природі. Один із прикладів – бджолині соти, які мають вигляд многокутника, покритого правильними шестикутниками. На цих шестикутниках бджоли вирощують із воску соти. В них бджоли відклада-ють мед, а потім знову накривають суцільним прямокутником із воску.

Соти можуть мати форму правильних трикутних, чотирикутних та шестикутних призм і кількість меду в сотах буде залежати від об’єму призми, а кількість воску, необхідного на ці соти, – від площі бічної поверхні призми

“Далі цієї сходинки досконалості в архітектурі природний відбір не міг йти, тому що соти бджіл абсолютно досконалі з точки зору економії праці і воску” Чарльз Дарвін З усіх правильних мно-гокутників тільки трикут-никами, квадратами і шестикутниками можна заповнити площину без пробілів і накладань. Тому, щоб заповнити вулик сотами без пустот, бджоли повинні були “вибрати “ одну із цих форм.

Об’єм меду, що міститься в одній комірці, буде залежати від площі основи комірки і її висоти. Тому, якщо ці комірки різної форми і однакової висоти, то меду в них буде вміщатися однакова кількість. Так як соти займають увесь вулик, то незалежно від того, яку вони мають форму, об’єм, тобто кількість меду, в них буде однаковий. Отже, вибір форми зв’язаний з кількістю воску, що витрачається на соти.

Як вже було сказано, кількість воску, необхідного для сот залежить від площі бічної поверхні призми, яка в свою чергу залежить від периметра основи призми і її висоти. Висоти у призм однакові, а ось периметри – різні. Знайшовши периметри правильного трикутника, чотирикутника і шестикутника з рівними площами, результати занесли в таблицю. І ось що одержали!

Порівняємо периметри різних многокутників з однаковими площами Вид многокутника Площа S Сторона а Периметр Р Трикутник Чотирикутник Шестикутник

“Інженерне мистецтво” бджолиної спільноти Отже, бджоли, не знаю-чи математики, вірно “визначили”, що пра-вильний шестикутник має найменший приметр серед фігур з рівними площами. Будуючи соти, бджоли інстинктивно намага-ються зробити їх об’єм-нішими, витративши при цьому якомога менше воску

Вчені не можуть пояснити такі “пізнання” бджіл в області геометрії Пояснення одне: для створення су-дини такої доско-налої форми робочі бджоли забезпечені унікальною врод-женою програмою і напрочуд складною, чітко координова-ною інстинктивною поведінкою

Надійні помічники агрономів Перелітаючи з квітки на квітку – бджоли запилюють рослини, чим сприяють найбільшій зав’язі плодів і поліпшенню їх якості

Крилаті “селекціонери” Тисячі тонн гречки, насіння соняшнику, фруктів і ягід одержують люди лише від того, що бджоли працюють у садах і на полях, коли цвітуть ці культури