Інтегрований урок за темою "Розв’язування задач на прогресії, у тому числі прикладного змісту"

9 клас

Інтегрований урок застосування знань на практиці.

Інтеграція: біологія

Тема. Розв’язування задач на прогресії, у тому числі прикладного змісту.

Мета:

• формування в учнів цілісного світогляду про навколишній світ;
• підвищення якості засвоєння матеріалу;
• створення творчої атмосфери;
• застосування знань про прогресії при вивченні біології.

Очікувані результати:

• здібність учнів до творчого поєднання знань математики та біології;
• уміння застосовувати знання у новій життєвій ситуації;
• виховувати життєві компетенції;
• розвивати логічне мислення та цікавість.

Хід уроку

1. Мотивація навчальної діяльності.

Знання з математики потрібні у житті. Математика дуже тісно пов’язана з фізикою, хімією, астрономією й економікою. На уроці ми застосуємо знання про прогресії для розв’язання задач пов’язаних з біологією.

2. Актуалізація знань.

Арифметична прогресія

(­­ – перший член; – різниця; – кількість членів; – -й член;

– сума перших членів)

Геометрична прогресія

( – перший член; – знаменник; – кількість членів; – -й член;

– сума перших членів)

Перегляд відеороликів:

1. Розподіл бактеріальної клітини

https://www.youtube.com/watch?v=qsxQwRIuBuA

https://www.youtube.com/watch?v=aU4exdTl7J8

https://www.youtube.com/watch?v=g9XGYO94Ot0

2. Розподіл інфузорії-туфельки

https://www.youtube.com/watch?v=YbUyC7UYYhA

https://www.youtube.com/watch?v=e2zYIc9FW_U

3. Основна частина уроку.

Учитель:

-У вас на партах лежать інтелект-картки, протягом уроку треба заповнювати порожню частинку картки, вписуючи інформацію про інтеграцію математики в біологію.

Поділ на групи відбувається за допомогою кольорових карток. Учні з червоними картками – перша група, з синіми – друга.

Робота в групах.

Завдання: кожна група повинна розв’язати по 4 задачі, вибрати доповідача й зробити звіт.

Перша група — 1 – 4 задача.

Друга група — 5 – 8 задача.

Послідовність Фібоначчі.

1;1;2;3;5;8…..

Перші два члени – одиниці, і кожний член, починаючи з третього, дорівнює сумі двох попередніх.»

Практичне застосування знань.

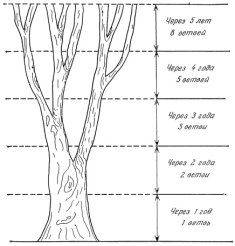Задача № 1.

Дерево зростає так, що кожна нова гілка в перший рік тягнеться до сонечка, а потім починаючи з другого року дає по одній бічній гілці. Скільки гілок буде на дереві через 1, 2, 3, 4 і т.д. років?

Розв’язання.

Нехай деяке дерево росте так, що кожна нова гілка в перший рік тільки тягнеться вгору або в сторону, а потім (починаючи з другого року) щорічно дає по одному боковому пагону. Питається, скільки гілок буде на дереві, яке виросло з саджанця без єдиного бічного пагона, через 1, 2, 3, 4 роки і т.д.? Таке дерево, яке виросло в повній відповідності з умовами завдання, зображено на рис. 1. У дворічного дерева є лише 1 гілка, у трирічного дерева число гілок зросте до 2, у чотирирічного - до 3, у п'ятирічного - до 5, у шестирічного - до 8. Якщо виписати ці числа поспіль, то вийде послідовність (1). Неважко зрозуміти, чому виконується правило, за яким будь-який член послідовності дорівнює сумі двох попередніх. Якого б віку не досягло дерево, число гілок у нього дорівнює сумі числа гілок, які були рік тому, і числа новопосталих бічних пагонів. Останнє ж в точності збігається з числом гілок, які були в дерева два роки тому, так як нові пагони могли пустити ті і тільки ті гілки, вік яких не менше двох років.

Задача № 2.

Достигла маківка повна крихітних зернинок, їх приблизно 3000. Скільки маків було б на землі, якщо кожне зернятко проросте через 5 років?

Розв’язання.

Це геометрична прогресія. ;

1 рік — рослин

2 рік —  рослин

4 рік — рослин

5 рік —

Поверхня усієї суші становить це ≈ у 2000 разів менше, ніж виросло маків.

Задача № 3.

Зробимо подібний розрахунок не для маку, а для будь-якої іншої рослини, яка дає менше насіння, ми дійшли б до такого ж результату, але тільки потомство її вкрило б усю Землю не за п’ять років, а за трохи більший строк. Візьмемо хоч би кульбабу, яка щороку дає 100 сім’янок.  Скільки кульбаб буде на всій земній суші через 9 років? І скільки кульбаб буде на кожному квадратному метрі?

Розв’язання.

За 1 рік            .   .   .   .  .   .   .  .   .   .  .   .   .  .   .   .  .   .   .  .   .   .   .   .   .  .   .           1  рослина

»   2 роки          .   .   .   .   .   .  .   .   .  .   .   .  .   .   .  .   .   .  .   .   .   .   .   .  .   .          100 рослин

»   3       »   .   .   .   .   .   .  .   .   .  .   .   .  .   .   .  .   .   .  .   .   .   .   .   .              10 000      »

»   4       »    .   .   .   .   .   .  .   .   .  .   .   .  .   .   .  .   .   .  .   .   .   .   .             1 000 000      »

»   5 років  .   .   .   .   .   .  .   .   .  .   .   .  .   .   .  .   .   .  .   .   .   .   .   .  .  100 000 000      »

»   6       »   .   .   .    .   .   .  .   .   .  .   .   .  .   .   .  .   .   .  .   .   .   .   .   10 000 000 000      »

»   7       »   .   .   .    .   .   .  .   .   .  .   .   .  .   .   .  .   .   .  .   .   .   .  1 000 000 000 000      »

»   8       »   .   .   .    .   .   .  .   .   .  .   .   .  .   .   .  .   .   .  .   .   .  100 000 000 000 000      »

»   9       »    .   .   .    .   .   .  .   .   .  .   .   .  .   .   .  .   .   .  .   . 10 000 000 000 000 000      »

Це у 70 разів більше, ніж є квадратних метрів на всій суші. Таким чином, на 9-й рік материки земної кулі були б вкриті кульбабами, по 70 на кожному квадратному метрі.

Задача № 4.

Нехай кожна муха відкладає 120 яєчок, а протягом літа встигає з’явитися 7 поколінь мух, половина яких – самиці. За початок першої кладки приймаємо 15 квітня  й будемо вважати, що муха-самиця за 20 днів виростає настільки, що сама кладе яєчка. Скільки з’явиться мух з 15 квітня до 1 вересня?

Розв’язання.

15 квітня – самиця відклала 120 яєчок; на початку травня – вийшло 120 мух, із них 60 самиць;

5 травня кожна самиця кладе 120 яєчок: у середині травня – виходить мух, із них 3600 самиць;

25 травня –  кожна з 3600 самиць кладе по 120 яєчок; на початку червня – виходить мух, із них 216 000 самиць;

14 червня – кожна з 216 000 самиць кладе по 120 яєчок; наприкінці червня виходить 25 920 000 мух, у їх числі 12 960 000 самиць;

5 липня – 12 960 00 самиць кладуть по 120 яєчок; у липні – виходить 1 555 200 000 мух, серед них 777 600 000 самиць;

25 липня – виходить 93 312 000 000 мух, серед них 46 656 000 000 самиць;

13 серпня – виходить 5 598 720 000 000 мух, серед них 2 799 360 000 000 самиць;

1 вересня – виходить 355 923 200 000 000 мух. Щоб краще уявити собі цю величезну кількість мух протягом одного літа, припустимо, що вони вишикувані у пряму лінію. Оскільки довжина мухи 5мм , то всі ці мухи простяглися б на 2500 млн. км — на відстань від Землі до далекої планети Уран.

Задача № 5.

У сприятливих умовах бактерії розмножуються так, що протягом 15 сек одна з них ділиться на дві. Укажіть кількість  бактерій, народжених однією бактерією за 7 хвилин?

Розв’язання.

Дано: геометрична прогресія . Знайти:

15 сек = ¼ хв.

Відповідь: 134217728 бактерій.

Задача № 6.

Бактерія, потрапивши в організм, до кінця 20 хвилини ділиться на дві, кожна з яких до кінця 20 хвилини знову ділиться на дві і т.д. Скільки бактерій буде в організмі через добу?

Розв’язання.

Кількість бактерій кожні 20 хвилин збільшується в 2 рази, тому маємо: 1,2,4,8, ... геометрична прогресія, у якій                         

За формулою знайдемо 

бактерій

Відповідь:      бактерій.        

Задача № 7.

Нехай у нас є одне зерно пшениці. Посадимо його в землю. З нього виросте рослина, у колосі якої буде 2 зерна. Висадимо їх знову і т. д. Скільки рослин у нас буде через 64 покоління?

Розв'язання.

Уявімо в вигляді прогресії. Дано: , . Знайти:

Відповідь: 9223372036854775808 рослин.

Задача № 8

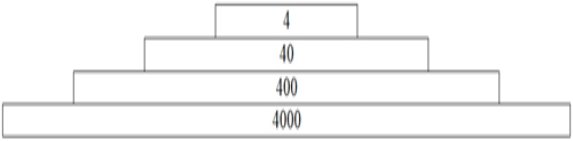
На узліссі живуть 4 куниці, які харчуються білками. Білки харчуються горіхами. Одна куниця з'їдає 10 білок. Для поліпшення родючості сосни потрібні ґрунтові бактерії. Скільки потрібно білок, горіхів, бактерій, щоб побудувати екологічну піраміду даної ділянки лісу, використовуючи геометричну прогресію.

Розв’язання.

;

Для екологічної рівноваги цієї ділянки лісу необхідно на 4 куниці 40 білок, 400 горіхів, 4000 бактерій.

Звіт представників груп.

Історична хвилинка з біології

1.В Америці  не було горобців. Цей такий звичайний у нас птах був завезений у Сполучені Штати з наміром знищувати  шкідливих комах. Горобець, як відомо, поїдає багато ненажерливої гусені та  комах, які завдають шкоди садам і городам. Нове оточення сподобалося горобцям: в Америці не знайшлося хижаків, які знищували б цих птахів, і горобець почав швидко розмножуватися. Кількість шкідливих комах почала помітно зменшуватися, але незабаром горобці так розмножилися, що — через нестачу тваринної їжи — прийнялися за рослинну, почали знищувати посіви. Довелося приступити до боротьби з горобцями.  Ця боротьба коштувала американцям так дорого, що надалі було видано закон, який забороняв завезення до Америки будь-яких птахів та тварин.

2.Другий приклад. У Австралії не існувало кролів, коли цей материк було відкрито європейцями. Кріль завезений туди наприкінці XVIII століття, і оскільки там немає хижаків, які живляться кролями, то розмноження пішло надзвичайно швидким темпом. Незабаром полчища кролів заповнили всю Австралію, завдаючи страшенної шкоди сільському господарству і перетворившися на справжнє лихо. На боротьбу з цим лихом сільського господарства було кинуто величезні кошти, і тільки завдяки енергійним заходам вдалося справитися з бідою. Приблизно те саме повторилося пізніше з кролями у Каліфорнії.

3.Третя навчальна історія сталася на острові Ямайці. Тут у великій кількості водилися отруйні змії. Щоб позбавитися їх, було вирішено завезти на острів птаха-секретаря, лютого винищувача отруйних змій. Число змій справді незабаром зменшилося, зате надзвичайно швидко розплодилися польові щури, яких раніше поїдали змії. Щури завдали такої шкоди плантаціям цукрової тростини, що довелося серйозно подумати про їх знищення. Відомо, що ворогам щурів є індійська мангуста. Вирішено було завезти на острів 4 пари цих тварин і дати їм вільно розмножуватися. Мангусти добре пристосувалися до нової батьківщини й швидко заселили весь острів. Не минуло й десяти років, як вони майже знищили на цьому острові всіх щурів. Та на жаль, знищивши щурів, мангусти стали годуватися чим трапиться, і зробилися всеїдними тваринами: нападали на цуценят, козенят, поросят, свійську птицю та поїдали їх яйця. А розмножившися ще більше, взялися за плодові сади, хлібні поля, плантації. Жителі приступили до знищення своїх недавніх спільників, але їм вдалося лише до деякої міри обмежити шкоду, якої завдавали мангусти.

Підсумок уроку.

Рефлексія

1. Які знання з математики ви застосовували при розв’язанні задач із біології?
2. Які знання з біології вам знадобилися для розв’язання математичних задач?
3. Заповніть інтелект-картки.

За законами математики побудована природа, законам математики підкоряється Всесвіт.