Інтелект-шоу в 8 класі по темі: "Діофантові рівняння"

        Інтелект-шоу в 8 класі по темі:

" Діофантові рівняння"

•                                 

з переважно середніми та низькими здібностями до вивчення математики був задуманий як урок-експеримент по вивченню деяких сторін загального інтелекту учнів за параметрами:

       І – числові індикатори-бали

ІІ – характеристика процесів розумової діяльності.

Форма проведення уроку-математичне кафе «Зустрічі, зустрічі...».

• з однокласницею, але через складання тотожностей
• з вченими минулого: Ейлером, Діофантом, Піфагором...
• з задачами з наукового багажу цих вчених, але на рівні     можливостей учнів 8 класу
• з незвичними рівняннями
• з квадратами, які звуться магічними
• з трійками, але піфагорійськими.

Додаю сценарій цього уроку, завдання, якого можна ускладнювати в залежності від рівня класу.

    Оформлення кабінету

• кабінет перетворюється у затишне кафе з кавою та печивом; новорічне оформлення;

музика Р. Паулюса.

• столик для жюрі, на якому листки з прізвищами учнів і назвою конкурсів, з вказаним максимальним числовим індикатором.
• на столах учнів листки досліджень інтелекту в яких фіксуються всі етапи розумової діяльності учнів та ще стіл мозкової атаки для бажаючих прийняти участь у “ важких ” конкурсах.

1. Хід уроку

Вступне слово учителя, після чого об’явлюється: конкурс №1 –

“Склади тотожність”

 

Ліва частина-картки для дівчат	Права частина-картки для хлопців
1)	1)
2)	2)
3)	3)
4)	4)
5)	5)
6)	6)
7)	7)
8)	8)
9)	9)
10)	10)
11)	11)
12)	12)
13)	13)

 

Ті пари, що склали тотожність за визначений час, підходять до столу жюрі і одержують бали.

І – пара по 5 балів

ІІ – пара по 4 бали

ІІІ – пара по 3 бали

IV – пара по 2 бали

Всі інші, які правильно склали тотожність, одержують по 1 балу.

Тим, хто розгубився, консультанти у жюрі допомагають знайти пару.

• Конкурс №2 “ Діофантове рівняння ”

а) Учень одягнутий під Діофанта розповідає його біографію-вірш, з якого учні повинні скласти рівняння і розв’язавши його знаходять скільки років прожив Діофант. Цей вірш був написаний на його могильній плиті:

 

Подорожній! Поховано тут Діофанта. І числа розкажуть тобі;

Який довгий шлях він пройшов. Шосту частину його становило веселе дитинство. Минула частина дванадцята – й пухом покрилося його підборіддя. Сьому в бездітному шлюбі прожив Діофант. Минуло п’ять літ. Ощасливлений він був народженням пер венця –сина. Якому судилося лише половина життя його батька. І в глибокій журбі старець закінчив свій шлях на землі, ще проживши років 4 з часу, коли сина не стало. Скажи: Віку якого досягши славетний прожив Діофант?

 

( 1/6х + 1/12х + 1/7х + 5 + 1/2х + 4 = х; х = 84 )

За певний час жюрі оцінює роботу.

Інформація вчителя. Діофант написав велику працю під загальною назвою “ Арифметика ”, що складається з 13 книг. Особливо цікавою була теорія рівнянь з цілими коефіцієнтами, розв’язки яких цілі, або раціональні. Ось діофантове рівняння першого ступеню: ах + by = c { a,b,c }ЄZ.

 

Розглянемо простеньку задачу, з умови якої можна скласти діофантове рівняння:

 

Скільки марок вартістю 40 коп. і 25 коп. можно купить на     5 грн., якщо у продавця немає здачі.

 

Позначимо х – кількість марок номіналом

40 коп.у – кількість марок номіналом 25 коп.

 

 

За умовою задачі х > 0, у > 0 I { х, у } Є N.

Рівняння:

40 х + 25 у = 500

8 х + 5 у = 100

у = ( 100 – 8 х ) / 5

 

Враховуючи допустимі значення х і у можна знайти тільки 2 розв’язки.

 

( х, у ) / { (5; 2) ; ( 10; 4 ) }

 

Конкурс №3

Пропонуються задачі на дослідження двох рівнів складності на діофантові рівняння

• а) Якими способами можна заплатити 79 грн., якщо маємо купюри 2 грн. та 5 грн. номіналу.
• б) На складі є цвяхи у ящиках місткістю 16 кг, 17 кг, 40 кг. Чи може комірник видати 100 кг цвяхів не розкриваючи ящиків.

Задачу б) розв’язують за столиком мозкової атаки, є можливість спілкування.

По закінченню певного часу жюрі перевіряє та оцінює роботи.

 

Вчитель оголошує відкрите засідання

 “піфагорійської школи ”.

За стіл мозкової атаки сідають учні з зірковими п’ятикутниками на одягу , це ознака піфагорійців.

 

Засідання веде учень

 

Розглядається Піфагорові рівняння або діофантове рівняння ІІ степеня х² + у² = z² { х, у,z } Є N. (1)

Використовуючи теорему – кожне непарне число є різницею послідовних квадратів, знаходять піфагорійські трійки           ( множину розв’язків рівняння (1)).

 

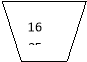
1 4 9                    36 49 64 81 100 121 

3 5 7                   11 13 15 17 19 21 23 

 

В нижній строчці знаходимо “квадратні” числа та знаходимо Піфагорійські трійки ( множину розв’язків ).

( х, у,z ) / { ( 3, 4, 5 ); ( 12, 5, 13 ) ....}

Якщо х непарне, краще знаходити за формулами:

Y = ( x² – 1 ) /2; z = ( х² + 1 ) /2;

Наприклад ( 9, 40, 41).

 

В загальному випадку складаються таблиці піфагорових трійок; використовуються інші формули:

 

х² + у² = z²

х² = ( х + у ) ( z – у )

 

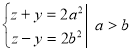
Приклад:

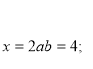
Конкурс №4 “Де риба?”

 

Два птаха сидять на верхівках дерев висотою 10 м та 15 м., що ростуть по різних берегах річки шириною 25 м.

 

На якій відстані від берегів  виринала на поверхню риба, якщо птахи одночасно опинилися біля неї?

 

 

 

 

 

 

 

 

 

 

 Позначимо ДО = х; ОС = у тоді

х = у = 25; х = 25 – у, але АО² = АD² + DО²;

ОВ² = ВС² + ОС²

АО = ОВ   15² + х² = 10² + у²; х = 10, у = 15

Відповідь: ДО = 10 м.; ОС = 15 м.

Жюрі оцінює

 

Подається печиво, кава

Оголошується математичне меню

 

Конкурс №5 “ Математичне меню ”

 

1 страва

суп харчо, який не їв ніхто

Щоб його замовити, треба підрахувати кількість складових частин: 1 морква, 2 цибулини, 3 картоплини...

1+ 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + ... + 50

 

2 страва “ Салат “Фантазер” – для його замовлення треба обрати на дошці вдалу відповідь на запитання

Запитання дає вчитель	Відповідь на дошці треба обрати
1. Інкогніто з математики	1. Безнадьога. точка. Ру.
2. Що загрожує неучу	2. х
3. Фронтальне опитування	3. Сова
4. Символ мудрості	4. Небезпека знову стати мавпою
5. До контрольної не готовий	5. один проти 30

 

Відповіді: (1– 2); (2 – 4); (3 – 5); (4 – 3); (5 – 1)

 

2. Страва – “ коктейль Фантазер ”

Для його замовлення треба виконати математичний танець           

тим хто зробив замовлення – нараховуються бали.

 

Слово жюрі – оголошуються результати

 

3. Страва – десерт – “Корона”:

Жюрі оголошують результати конкурсів.

Вручаються сувеніри: сова, як символ мудрості, грамоти, солодкі призи, учні танцюють під музику Вівальді.

 

Збираються листки досліджень на інтелект для обробки одержаної інформації.

 

При наявності часу можна ознайомити учнів з деякими цікавими задачами, які вперше ввів

Леонард Ейлер ( 1707 – 1783 ).

Вони пов’язані з магічними та латинськими квадратами, теорією графів.

 

Інформує учитель

Магічні квадрати – це квадратні таблиці натуральних чисел розміром п х п , в яких певним чином розташовані числа: суми чисел по горизонталі, по вертикалі та по діагоналі рівні. Цікаво те, що магнічного квадрату розміром 2 х 2 не існує, а розміром 3 х 3 існує тільки один:

 

 

2	9	4
7	5	3
6	1	8

 

Конкурс № 1 : 3 магічного квадрату розміром 3 х 3 ( мал. 1) одержати інші відображення від осей симетрії, або поворотом біля центру.

 

Латинські магічні квадрати характеризуються тим, що числа в квадраті не повторюються. Якщо при наладанні двох латинських квадратів один на одного, всі одержані пари чисел різні, такі латинські квадрати вважають ортогональними.

 

З ортогональними латинськими квадратами пов’язана задача, яку вперше розв’язав Ейлер:

 

Серед 25 офіцерів порівну уланів, драгунів, гусарів, кавалеристів та гренадерів, а також порівну генералів, полковників, майорів, капітанів, поручиків причому кожний рід військ представлений офіцерами всіх 5 рангів. Чи можна вистроїти цих офіцерів в квадрат 5 х 5, щоб в кожній колоні і  в кожній шерензі зустрічались офіцери всіх 5 рангів.

 

На цю задачу краще підготувати кольоровий плакат.

 

Аналогічна задача для 36 офіцерів не була розв’язана Ейлером, але в 1901 р. було доведено, що ортогональних квадратів розміром 6 х 6 не існує.

 

Теорія латинських квадратів знайшла застосування не тільки в самій математиці, а і у галузях народного господарства.