Інтелектуальна гра для учнів 8 класу "Математичний турнір"

Інтелектуальна гра «Математичний турнір»

Мета: поглибити і розширити знання учнів з математики; розвивати пізнавальний інтерес, логічне мислення учнів, допитливість, творчу активність.

Девіз:  «Предмет математики настільки серйозний, що не варто втрачати нагоди зробити його трохи цікавішим».                      Блез Паскаль

Хід гри

У грі беруть участь учні 8 класів. Учні розповідають про себе, займають місця за ігровими столами. Розпочинається відбірковий тур, за результатами якого визначають, у якій послідовності учасники будуть обирати теми та відповідні запитання.

 У кожній із запропонованих тем – кути, трикутники, кола, тригонометрія, рівняння, історія математики – 8 запитань. Кожне запитання 1 бал. Якщо учень дає правильну відповідь на всі запитання, то він отримує додатково ще  5 балів. Якщо учень відповів на одне з них неправильно, то припиняє подальшу участь у цьому конкурсі.

 У фінальному конкурсі визначають найсильнішого учасника.

Відбіркова гра

1. Давньогрецький математик, автор книги «Початки». (Евклід)
2. Розв’язати рівняння |х-2|=-5 ()
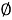
3. Геометричне місце точок, координати яких задовольняють рівняння х²+у²=100. (Коло)
4. Яке ціле число без остачі ділиться на будь-яке інше число? (0)
5. На яке число слід поділити 2, щоб дістати 4? (На ½)
6. Точка перетину висот трикутника знаходиться в середині трикутника. Який це трикутник? (Гострокутний)
7. Один з найдавніших обчислювальних приладів. (Пальці)
8. Що більше а чи 2а? (а>0, а<2а; а<0, а>2а)

Історія математики

1. Йому приписують вислів: «Все є число». До числа він хотів звести весь світ і математику. На його дослідження великий вплив мала філософія та релігія Сходу. Він вперше розділив числа на парні і непарні, прості і складені. (Піфагор)
2. Відомий український математик, методи якого використані в США, Японії та інших країнах при моделюванні кібернетичної техніки. Наукові праці цього вченого широко використовували американські автори першого у світі комп'ютера. (М.П.Кравчук)
3. Першим написав книгу арабською мовою про розв’язування рівнянь, де вперше прозвучало слово «алгебра». (Мухаммад ібн Муса ал-Хорезмі)
4. Він був знаменитим математиком, його називали «батьком алгебри». Він настільки захоплювався математикою, що інколи засиджувався до трьох діб без сну та їжі. (Вієт)
5. Видатний український математик, механік, фізик, член-кореспондент Паризької Академії наук, Російської, Туринської, Римської, Американської академій, почесний доктор Київського, Московського та багатьох інших університетів. Приятелював з Тарасом Шевченком. (М.В.Остроградський)
6. Він прожив 25 років. Лише 5 років займався математикою. Математичні роботи, які прославили його ім’я, займають 60 сторінок. Йому було 17, коли вчитель сказав: «Він працює лише у вищих галузях математики». (Галуа)
7. Про себе він говорив: «Я навчився рахувати раніше, ніж читати». Сучасники розуміли його велич, про що свідчить напис на медалі «Король математики». (Гаусс)
8. Український математик, який розв'язав п'яту узагальнену проблему Гільберта, одну з найскладніших в сучасній алгебрі. Важливі результати дістав в теорії цифрових автоматів, в галузі застосувань обчислювальної техніки в керівництві виробничими процесами та економіці. Під його керівництвом були створені універсальні електронно-обчислювальні машини "Київ", "Дніпро", серії машин „Мир” та інші ЕОМ. (В.М.Глушков)
9. Перший давньогрецький філософ і математик, вчитель Піфагора, автор теореми про пропорційні відрізки. (Фалес)

Кути

1. Який кут називають розгорнутим? (180⁰)
2. В яких одиницях вимірюють кути? (Градус, радіан)
3. Як називають прямі, що перетинаються під прямим кутом? (Перпендикулярні)
4. 2²=4, 3²=9, а чому дорівнює кут у квадраті? (90⁰)
5. Як називаються сторони прямокутного трикутника, які утворюють прямий кут? (Катети)
6. Відношення протилежного катета до гіпотенузи у прямокутному трикутнику називається… (Синусом кута)
7. Сторона навпроти прямого кута в прямокутному трикутнику називається… (Гіпотенуза)
8. Яка властивість кутів рівнобедреного трикутника? (Кути при основі рівні)
9. Скільки мінут у одному градусі? (60)

Трикутники

1. Трикутник, у якого дві сторони рівні, називається… (Рівнобедреним)
2. Яка сторона в рівнобедреному трикутнику називається основою?
3. Прямокутний трикутник зі сторонами 3,4.5 одиниць називається… (Єгипетським)
4. Яка фігура називається трикутником?
5. Теорема, названа на честь математика і стосується прямокутного трикутника. (Теорема Піфагора)
6. Яку властивість має медіана, проведена до основи в рівнобедреному трикутнику?
7. Відношення протилежного катета до прилеглого в прямокутному трикутнику називається… (Тангенсом кута)
8. Чи можна побудувати трикутник зі сторонами 9м, 11м і 24м?

Коло

1. Яка пряма називається дотичною до кола?
2. Яке коло називається описаним навколо трикутника?
3. Де заходиться центр кола, описаного навколо трикутника?
4. Що називається діаметром кола?
5. Чому дорівнює відношення довжини кола до діаметра?
6. Де знаходиться центр кола, вписаного в трикутник?
7. Що таке центральний кут?
8. Як обчислити довжину кола?
9. Що таке вписаний кут?

Чотирикутники

1. Яка фігура називається чотирикутником?
2. Що таке діагоналі чотирикутника?
3. Як називається чотирикутник, у якого діагоналі перетинаються і точкою перетину діляться навпіл?
4. Що таке прямокутник, його властивості?
5. Що таке ромб, його властивості?
6. Що таке квадрат, його властивості?
7. Який чотирикутник називається трапецією?
8. Чому дорівнює середня лінія трапеції?
9. Що називається паралелограмом?

Тригонометрія

1. Основна тригонометрична тотожність. (cos²α+sin²α=1)
2. cos 30^o=… (√3/2)
3. sin 60^o=…(√3/2)
4. Як виражається катет прямокутного трикутника через гіпотенузу і гострий кут? (a=csinα)
5. Як виражається катет прямокутного трикутника через гострий кут і другий катет?
6. Чому дорівнює sin(90^o-α)? (cos α)
7. sin 45^o=… (√2/2)
8. Що називається косинусом гострого кута прямокутного трикутника?

Рівняння

1. Що таке рівняння?
2. Які рівняння називають лінійними?
3. Що являє собою графік лінійного рівняння з двома змінними?
4. Які рівняння називають рівносильними?
5. Що означає розв’язати рівняння?
6. Які рівняння називають квадратними?
7. Що таке дискримінант квадратного рівняння?
8. Сформулюйте теорему Вієта.
9. Що називається розв’язком рівняння з двома змінними?

Фінал

1. З трьох спроб учасники повинні відгадати, про яку теорему йдеться у підказках. За правильну відповідь після першої підказки учасники отримують 3 бали, після другої – 2 бали, після третьої – 1 бал.

Перша підказка.

Важливість цієї теореми ілюструє такий цікавий факт. Наприкінці ХІХ ст. на Марсі було відкрито «канали», які тривалий час вважалися штучними. Для налагодження зв’язку з марсіанами вчені запропонували на величезному просторі Західносибірської рівнини побудувати гігантську геометричну фігуру, яка б світилася у вершинах, бо вважали, що теорема, яку ілюструє фігура, справедлива скрізь і що жителі будь-якої планети повинні зрозуміти такий сигнал. Вони сподівалися, що, побачивши зображення, марсіани зроблять висновок, що на Землі живуть розумні істоти і проінформують про це також мовою математики (адже математику вважають універсальною мовою Всесвіту!) По яку теорему йдеться?

На обдумування 30 с.

(Учні записують варіанти відповідей і віддають їх журі.)

Друга підказка.

Стародавні єгиптяни. Вавилоняни та інші народи стародавнього Сходу ще за 2000 р. до н.е. знали про божественну властивість числа 5, її використовували землеміри та будівельники. З історії відомо, що ця теорема зустрічається у вавилонських текстах, які було написано за 1200 років до того, як це зробив автор теореми. Знали її і в Стародавній Індії. На обдумування 30с.

Третя підказка.

Ця теорема має дуже широке практичне застосування. За допомогою неї можна геометрично знаходити значення квадратних коренів з цілих чисел, а також визначати степені цілих чисел. У наш час нараховується більш ніж 100 доведень цієї теореми.

Правильна відповідь – теорема Піфагора.

2. Про одне й те саме число було зроблено такі заяви:

а) воно є точним квадратом;

б) у ньому три цифри, причому дві з них однакові;

в) сума його цифр дорівнює 9;

г) воно ділиться на суму своїх цифр без остачі. Назвіть число. (144)

Підводяться підсумки гри. Оголошується переможець.