Урок (конспект уроку з геометрії для 8 класу на тему "Середня лінія трапеції. Властивості середньої лінії трапеції").

Тема уроку.  Середня лінія трапеції. Властивості середньої лінії трапеції.

Мета уроку: ввести поняття «середня лінія трапеції», довести теорему про властивість середньої лінії трапеції; розвивати вміння розв’язувати задачі, застосовуючи теорему про середню лінію трапеції; формувати вміння учнів застосовувати здобуті знання на практиці та показати практичне застосування геометрії в повсякденному житті; формувати просторові уявлення, розвивати логічне мислення.

 

Епіграф: «Розум людський має три ключі, що все відмикають: знання, думку, уяву» (В. Гюго).

 

ХІД УРОКУ

1.           Організаційний момент.
2.        Мотивація навчальної діяльності.

Сьогодні наш урок присвячено трапеції. Дайте, будь ласка, означення трапеції українською, російською та англійською мовами.

Існує особлива мова, що зрозуміла кожній людині, якою б мовою та не володіла. Це – рисунок. Сьогодні на уроці ми будемо постійно звертатися до рисунків, розв’язувати задачі за готовими рисунками. Ви продемонструєте вміння застосовувати знання під час розв’язування задач на трапеції.

3. Актуалізація опорних знань (слайд 1).

 

 

 

 

 

 

 

 

 

Запитання до учнів:

1. Чим є для даного трикутника відрізок  MN?
2. Дайте означення середньої  лінії трикутника.
3. Назвіть властивість середньої лінії трикутника.
4. Сформулюйте теорему Фалеса.
5. Що можна сказати про довжину відрізків В₁В₂  і В₂С?
6. На які фігури поділяє трикутник АВС відрізок MN?
7. Який чотирикутник називається трапецією?
8. Які ж добудови можемо робити при розв’язуванні задач?

(використання програмного забезпечення

GeoGebra)  

 

 

  

 

  

 

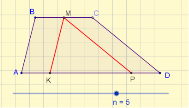
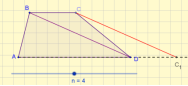
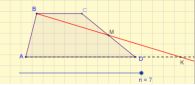
4. Проблемне питання.

Умова задачі (слайд 2):

Над входом у дачний будинок є навіс. Згодом виникла потреба поставити підпори до середини навісу. Як, не вимірюючи, можна знайти довжину підпори, якщо відповідні краї навісу віддалені від поверхні землі на 2,5 м і 3,5 м?

Поміркуйте і зробіть геометричний малюнок до цієї задачі так, щоб за готовим кресленням ми могли розв’язати задачу.

 

 

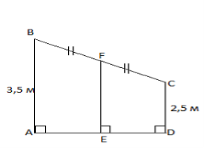
Мал.1

  Як ви вважаєте, чи можна на практиці, не застосовуючи безпосередню вимірювання, а використовуючи тільки знання з геометрії, визначити довжину підпори?

 На це питання ми зможемо дати відповідь, після того як розглянемо тему «Середня лінія трапеції. Властивості середньої лінії трапеції» (слайд 3).

5. Вивчення нового матеріалу.

1. Сформулювати означення  середньої лінії трапеції (слайд 4).

 

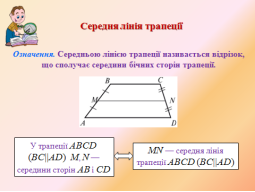
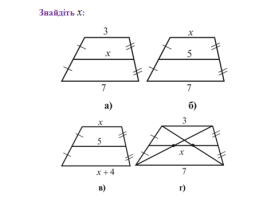
Усні вправи (слайд 5) .

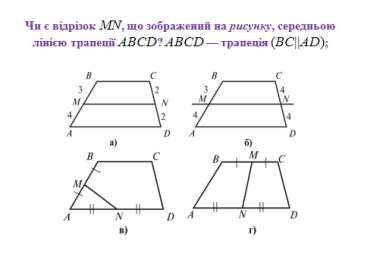
 На (рис. г) відрізок MN називається другою середньою лінією трапеції  і знаходиться за формулами MN = (AD-BC) або MN =(АВ + CD)

(слайд 6)

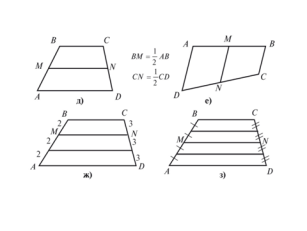
2. Сформулювати та довести властивість середньої лінії трапеції (використання програмного забезпечення GeoGebra).

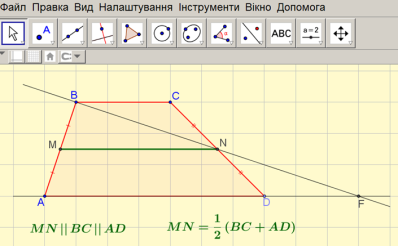
Усні вправи (слайд 7).

(слайд 8)

 

 

 

 

 

 

 

6. Розв’язування вправ за допомогою програми

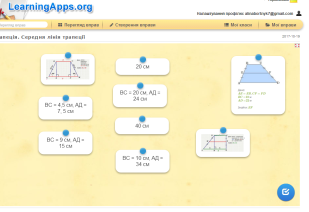
7. Розв’язування задач, які є властивостями середньої лінії трапеції.

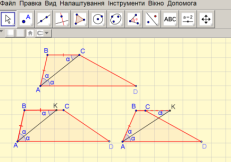
Задача 1. (Розв’язати задачу кількома способами, обґрунтувати раціональність та правильність свого вибору).

У рівнобічній трапеції  ABCD  MN – середня лінія, з вершини В на основу AD опущена висота ВК. Довести, що відрізок KD дорівнює середній лінії трапеції (слайд 9).

 

 

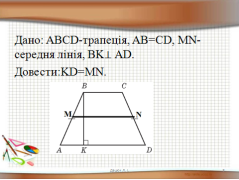
Перший спосіб. Перша група пропонує довести дану рівність провівши відрізок СЕ ВК, та використавши властивість середньої лінії трапеції (слайд 10).  

 

                       

Другий спосіб.  Провести уАВКмедіану МК, розглянути чотирикутник MNDK, довести що він – паралелограм, за його властивостями з’ясувати, що KD = MN (слайд 11).

 

 

Третій спосіб (слайд 12).  

 

 

Задача 2 (394)

(використання програмного забезпечення GeoGebra)

 

 

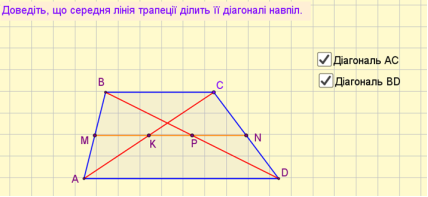
Задача 3 (слайд 13).

 

    Задача 4.

(використання програмного забезпечення GeoGebra)

 

 

 

 

 

 

 

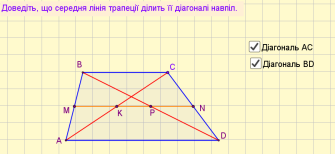
Задача 5.

(використання програмного забезпечення GeoGebra)

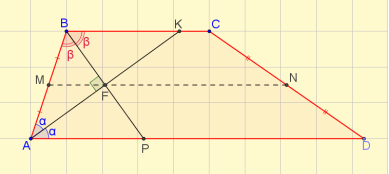
Задача 6 (слайд 14).

7.        Розв’язування «проблемної задачі» (слайд 15)

1. Учні пояснюють, чому саме такий малюнок (чому треба зобразити прямокутну трапецію, чому FE – середня лінія).

2. Обчислюють довжину підпори  FE як довжину середньої лінії трапеції.

FE = (2,5+3,5)/2.

Відповідь: довжина підпори 3 метри.

 

VIII. Застосовування вмінь та навичок. Виконання практичних завдань (слайд 16)

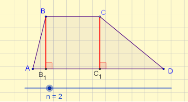
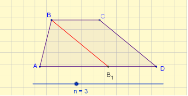
 Уявіть, що ви будівельники. Як знайти довжину паркану (тобто периметр трапеції ABXC), яким огороджено дитячий майданчик, якщо вершина X недоступна та купою піску частково присипано сторони BX і XC (див. рис.)? Ви повинні поміркувати та розв’язати цю проблему. (Учні працюють у парах)

Розв’язання:

1. Поділити сторону AB на три рівні частини та провести прямі KK1, MM1 паралельно AC.
2. Виміряти M1C, тоді XC=3M1C
3. Виміряти AC, MM1 та знайти BX.

 

                        В                                     Х

                 

                   К                                               К₁

 

             М                                                      М₁

 

             А                                                         С

IX. Підсумок уроку (слайд 17).

Вправа «Відшукай помилку» .

• Середня лінія трапеції сполучає середини двох сторін трапеції.
• Середня лінія сполучає середини основ трапеції.
• Середня лінія трапеції сполучає бічні сторони трапеції.
• Середня лінія трапеції дорівнює сумі основ.
• Середня лінія трапеції дорівнює півсумі сторін трапеції.
• Середня лінія трапеції паралельна до сторони трапеції.
• Середня лінія трапеції проходить через точку перетину діагоналей трапеції.

Домашнє завдання:

п.8, вправи № 244, 245, 247.