Розробка уроку геометрії в 8 класі на тему: «Розв’язування задач на застосування подібності трикутників»

Розробка уроку геометрії в 8 класі на тему: «Розв’язування задач на застосування подібності трикутників»

Тема: Розв’язування задач на застосування подібності трикутників

Мета: освітня: продовжити формувати вміння і навички учнів застосовувати вивчені ознаки подібності трикутників до розв’язування задач, удосконалити навички розв’язування задач практичного змісту;

розвиваюча: розвивати логічне мислення, математичну грамотність мовлення, культуру креслень;

виховна: виховувати пізнавальну активність, культуру спілкування, формування культури праці, сумлінного ставлення до матеріальних і духовних цінностей.

Тип уроку: формування вмінь та навичок.

Обладнання: комп’ютер, презентація, роздатковий матеріал, аркуш самоконтролю, креслярське приладдя.  

Епіграф уроку.

Навчання мистецтву розв’язувати задачі – це виховання волі.

(Д. Пойа)

Очікувані результати:

Після уроку учні зможуть:

• дати означення подібних трикутників;
• формулювати ознаки подібності трикутників та ознаки подібності прямокутних трикутників;
• свідомо застосовувати вивчений  матеріал під час розв’язування задач;
• робити логічні висновки, аналізувати вивчений матеріал;
• творчо мислити та самостійно працювати.

Хід уроку

1.      Організація класу

1.     Привітання з класом.
2.     Учні готуються до уроку.
3.     Психологічне налаштування учнів на роботу. Релаксація.

Учитель. Покладіть руки на парту або на коліна. Очі заплющені, тіло розслаблене, дихання повільне, ритмічне. Уявіть простір навколо себе. У кожний бік зверніть побажання (учитель промовляє слова, учні повторюють їх про себе):

                «Миру, любові, добра всім, хто праворуч.

                 Миру, любові, добра всім, хто ліворуч.

                 Миру, любові, добра всім, хто попереду.

                 Миру, любові, добра всім, хто позаду.»

Розплющте очі, посміхніться один одному, почнемо урок із гарним настроєм, повні сил.

2.                 Мотивація навчальної діяльності, повідомлення теми, мети уроку.

Тема нашого уроку « Розв’язування задач на застосування подібності трикутників», тому епіграфом до уроку я взяла слова великого Пойа «Навчання мистецтву розв’язувати задачі – це виховання волі». Видатний французький математик Жан Лерон Д’аламбер помітив, що «математика щедра, вона часто дає більше, ніж у неї просять».

Уявіть собі, що ви пішли зустрічати Новий рік у ліс. Побачивши найвищу ялинку, вирішили її прикрасити гірляндою і, головне, яскравою зіркою.  Знаючи свої фізичні можливості, ви зрозуміли: щоб не витрачати зайвих зусиль, потрібно спочатку з’ясувати чи це можливо.

Проблема? Так! Наше життя складається із таких маленьких проблем, які ми можемо на сьогоднішній день розв’язати, використовуючи ті знання, яких набуваємо під час уроків.

Отже маємо конкретну мету: знайти висоту ялинки, не піднімаючись на вершину.

Мета уроку – навчитисязастосовувати ознаки подібності трикутників до розв’язування задач. І я сподіваюсь, що наприкінці уроку ви зможете розв’язати цю проблему.

3.             Актуалізація опорних знань

Інтерактивна технологія «Інтерв’ю».

Один «учень-журналіст» збирає матеріал для математичної стіннівки. Які трикутники називаються подібними?

• Сформулюйте ознаку подібності трикутників за двома кутами.
• Сформулюйте ознаку подібності  трикутників за трьома сторонами.
• Сформулюйте ознаку подібності трикутників за двома сторонами і кутом між ними.
• Сформулюйте ознаки подібності прямокутних трикутників.
• Який досвід ти здобув, спілкуючись із учителем?
• Що б ти побажав однокласникам?

Отже, ми повторили ознаки подібності трикутників, а зараз пропоную застосувати ці знання до розв’язування базових задач, які нам допоможуть у більш складних ситуаціях.

Умови задач пропонуються у вигляді презентації. Учні розв’язують задачі усно, із докладними міркуваннями та коментарями. Обрані літери правильних відповідей учні записують у зошити. Потрібно скласти ключове слово із літер правильних відповідей до задач.

Задача №1

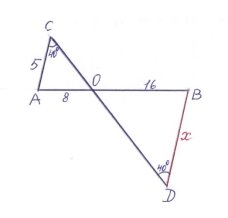    Знайти х

Розв’язання. ∆АCO~ ∆BDO за двома кутами.

Відповідь: 10

Задача №2

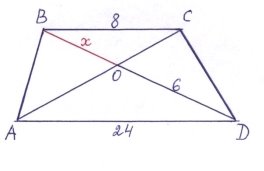   Знайти х

                                                 Розв’язання

за двома кутами. = ;   = ;  x = = 2.

                                                                        Відповідь: 2.

Задача №3

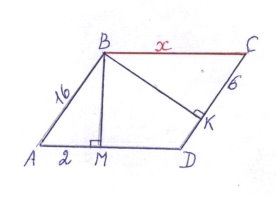  ABCD – паралелограм. Знайти х

                                                   Розв’язання

Трикутники  ABM і  CBK прямокутні, подібні за гострим кутом (А = за властивістю паралелограма).

= ;   = ;  x = = 48.

                                                                          Відповідь: 48

Яке слово зашифроване?

Яке слово було зашифроване? (Фалес)

Ми не вперше на уроках геометрії зустрічаємось з ім’ямдавногрецького математика, філософа Фалеса Мілетського.

Презентація «Фалес Мілетський−«колумб» математики»

Ще раз хочу нагадати, що саме узагальнену теорему Фалеса було покладено в основу вивчення подібності фігур, що дало змогу розв’язати багато практичних задач.

ІІІ. Формування вмінь і навичок.

Задача №480 (Г. П. Бевз, Геометрія−8)

Слайд 6.

За рисунком знайдіть відстань АВ, якщо АС=300м, DC=10м, ВС=360м, СF=12м, DF=13м.

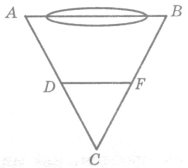    Розв’язання. Розглянемо  ∆АВС і ∆DCF.

Тому  ∆АВС~ ∆DFC за двома сторонами і кутом між ними. Отже

AB=30×13=390(м).

                                                        Відповідь: 390 м

Задача №44.(О. В. Погорєлов, Геометрія 7−9)

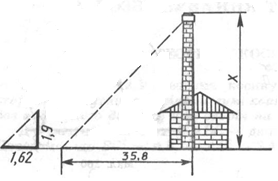Довжина тіні фабричної труби дорівнює 35,8 м. У той самий час вертикально поставлена жердина завдовжки 1,9 м дає тінь довжиною 1,62 м. Знайдіть висоту труби.

Розв’язання. Зробимо математичну модель до задачі

    B                    ВС−труба, АС− тінь труби,

                                                         МК− жердина, АК− тінь жердини.

М                              ВС

              K                          

С             К            А                 ∆АВС ~ ∆АМК,

 х=

Чи можемо ми з вами дати відповідь на поставлене на початку уроку питання: як виміряти довжину ялинки?

Якщо учні не запропонують цього способу, то вчитель розповідає як це зробити. У лісі можна знайти жердину, увіткнути її в землю. Дочекатися, коли тінь від ялинки і тінь від жердини збігатимуться. Тоді ми розглянемо відношення й знайдемо висоту ялинки.

4.              Діагностика знань і умінь. Самостійна робота.

Варіант 1.

1.                   Дано ∆AВF~∆CDF. Якщо АВ=12см, АF=8см,СF=6см, то CD дорівнює …(4б)

В

   С                 

                                                        А.8см.   Б.9см.   В.11см.   Г. Інша відповідь.

А                                  

D

2.               Доведіть подібність трикутників  ABC  і  DKF. (4б)

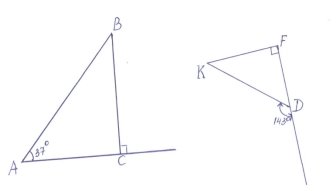
3.Відкрита ділянка дороги має ширину АВ = 10м. Пункт спостереження знаходиться на вежі висотою MN = 30м. На відстані 150м від вежі вздовж дороги побудовано паркан. Якої висоти він повинен бути, щоб закривати дорогу від спостерігача на вежі. (4б)

Варіант 2.

1. Дано: ABCD−трапеція. ∆ВОС~∆АОD. Якщо АD=16см, АО=6см, то менша основа ВС дорівнює … (4б)

A                   D                А.8,5см.   Б.9,6см.   В.10см.   Г.Інша відповідь.

    B               C

3. Доведіть подібність трикутників  ABC і  DKF. (4б)

3.Тенісний м’яч, що подали з висоти 2м10см, пролетів по прямій над самою сіткою, висота якої 90см. На якій відстані від сітки м’яч удариться об землю, якщо його подали з лінії, що знаходиться на відстані 12м від сітки? (4б)

V. Підсумки уроку. Домашнє завдання.

Чи можемо зробити висновок: ознаки подібності трикутників дають можливість вирішити багато практичних питань?

Домашнє завдання:

1.Повторити п.19,20.

2.Розв’язати задачі №6(а), 7(а), ст.130

3.Творча задача.

У 7 класі на уроках фізики ви вивчали закони відбиття світла та використовували їх для побудови зображення в дзеркалі. Спробуйте застосувати свої знання з фізики та геометрії для розв’язування такої задачі:як можна визначити висоту сосни за допомогою дзеркала?

Картка контролю