Урок (конспнкт уроку з геометрії для 8 класу на тему "Центральні та вписані кути")

Тема уроку. Центральні та вписані кути

Мета уроку: сформувати поняття центрального та вписаного кутів; довести теорему про вписані кути; вчити застосовувати отримані теоретичні знання під час розв'язування задач; розвивати вміння робити припущення, працювати з текстом і використовувати необхідну інформацію, правильно і чітко висловлювати свої думки; виховувати позитивне ставлення до навчання, наполегливість у досягненні мети.

Хід уроку

I. Організаційний момент.

II. Перевірка домашнього завдання.

3.         Формування теми, мети і завдань уроку. Мотивація навчальної діяльності.

• Які види кутів ви вже знаєте?

• Прямі
• Гострі
• Розгорнуті
• Тупі
• Вертикальні
• Суміжні
• Зовнішні
• Внутрішні односторонні
• Внутрішні різносторонні
• Відповідні

Отож, кутів ви знаєте вже багато, але для того щоб розв’язати задачу, (слайд 1)

 

 

ми повинні вивчити ще один вид кутів та їх властивості. Тож розпочинаємо вивчення нової теми.

Тема уроку: «Центральні та вписані  кути». (слайд 2)

Тема є важливою в курсі геометрії. Знання властивостей центральних та вписаних кутів будуть необхідні при вивченні теми «Вписані чотирикутники», а також при розв’язуванні задач стереометрії.

4. Актуалізація опорних понять.

Пригадаємо ті теоретичні відомості, які будуть необхідні при вивченні нового матеріалу:

1. Що називають кутом?
2. Назвіть елементи кута?
3. Який кут називається розгорнутий?
4. Який кут називається прямий?
5. Який кут називають зовнішнім кутом трикутника?
6. Яка властивість зовнішнього кута?

Також ми будемо використовувати коло, тому пригадаємо:

1. Що називають колом?
2. Що називають радіусом кола?
3. Що називають діаметром кола?
4. Що називають дугою кола?

 

5. Вивчення нового матеріалу.
   1. Практична робота ( в парах)

На ваших стола є аркуш, на якому зображені кола. Пропоную вам показати усі можливі взаємні розміщення кола та кута. Перший ряд будує тільки гострі кути, другий – прямі, третій – тупі. Працюючи в парі з сусідом по парті, обговоріть, де може розміщуватися вершина кута, та організуйте вашу співпрацю так, щоб зображення не повторювалися.(Учні виконують побудову кутів) 

2. Введення поняття центрального кута.

•  Чи є серед ваших малюнків схожі на ті, що зображені на слайді? Що їх об’єднує? ( слайд 3)

• Означення центрального кута (центральним кутом кола називають кут з вершиною у центрі кола).
• Дуги та їх позначення  (слайд 4)  (позначення     АВ відноситься до дуги, якій точка М не належить).
• Дати поняття вислову: «Центральний кут спирається на дугу».
• Градусна міра (Кожна дуга, як і все коло, має градусну міру. Градусною мірою дуги кола називають градусну міру відповідного центрального кута. Градусну міру всього кола вважають рівною 360°)
• Дуга, яка називається півколом.
• Пояснення вислову «хорда стягує дугу». (Будь-яка хорда стягує дві дуги, сума градусних мір яких дорівнює 360°).

3.   Введення поняття вписаного кута.

•               Яка особливість об’єднує кути у четвертому рядку?

(слайд 5)

•   Означення вписаного кута (вписаним кутом кола називають кут, вершина якого належить колу, а сторони перетинають коло).

(використання програмного забезпечення GeoGebra);

 

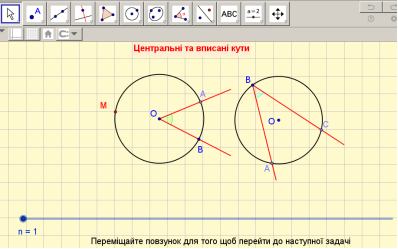
• Дуга, на яку спирається кут.

 

4. Властивість вписаного кута. Доведення теореми

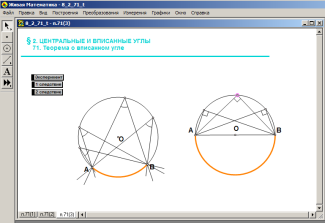
Розглянемо властивість, яка поєднує вписаний та центральний кут. ( слайд 6)

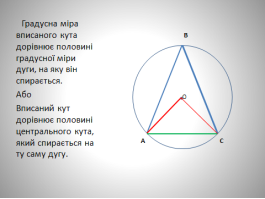
Для доведення теореми необхідно розглянути три випадки розміщення центра кола відносно сторін вписаного кута.(Теорія. Вписані кути. 71-2)

(використання програмного забезпечення «Жива математика)

 

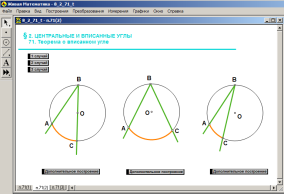
 Ще раз розглянемо залежність вписаного кута від градусної міри центрального кута.

(використання програмного забезпечення GeoGebra)

 

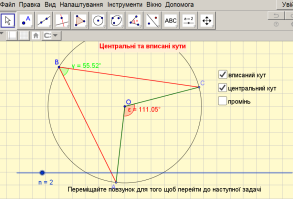
5. Наслідки з теорем

! Вписані кути, які спираються на одну й ту саму дугу, рівні.

! Вписаний кут, який спирається на діаметр (півколо), - прямий, і навпаки: будь-який прямий вписаний кут спирається на півколо. (Теорія. Вписані кути. 71-3)

(використання програмного забезпечення «Жива математика)

6. Осмислення нового матеріалу
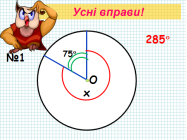
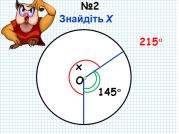
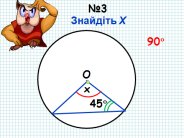
   1.               Колективне розв’язання усних задач під керівництвом учителя.

Кажуть, що загублений той час, який не використовується для навчання, а для математики найкраще навчання – розв’язування задач. Попрацюємо над розв’язуванням задач за готовими малюнками.

 

   

 

    

                 

    

 

               

 

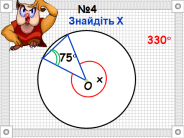
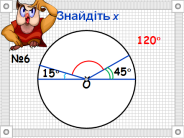
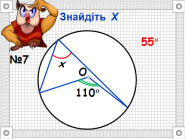
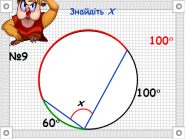
2.               Розв’язування задач з підручника.

№287.

Задача 1. (Базова задача, n=1)

(використання програмного забезпечення GeoGebra);

 

 

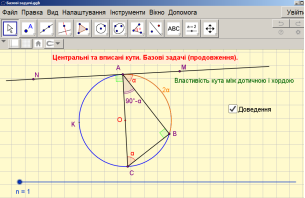
№290.

№292.

№297.( Базова задача, n=2)

(використання програмного забезпечення GeoGebra);

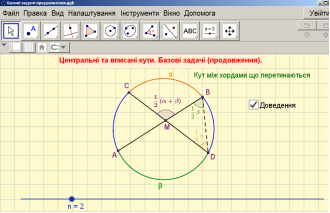
№298. ( Базова задача, n=3)

(використання програмного забезпечення GeoGebra);

 

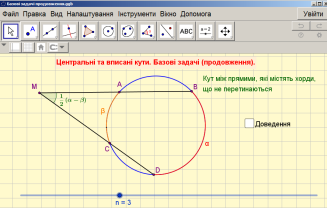
№304.(«Жива математика» №659, вписані кути)

(використання програмного забезпечення «Жива математика)

 

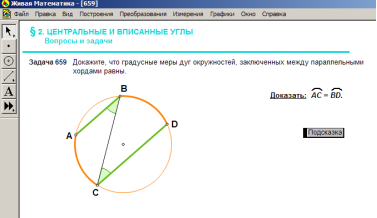
Задача 2.

(використання програмного забезпечення GeoGebra);

3.               Розв’язування задачі про футболіста.
4.               Графічний диктант.

1. Коло, що проходить через три вершини трикутника, є основним навколо даного трикутника. (Так)
2. Радіус – це відрізок, який сполучає дві точки кола. (Ні)
3. Відрізки дотичних, проведених з однієї точки до кола, рівні між собою. (Так)
4. Градусною мірою центрального кута є градусна міра відповідної дуги кола. (Так)
5. Вписані кути, що спираються на діаметр, не завжди є прямими. (Ні)
6. Сума протилежних кутів вписаного чотирикутника дорівнює 180°. (Так)
7. Якщо центральний кут спирається на дугу, яка становить ¼ кола, то його величина дорівнює 45°. (Ні)
8. Якщо градусна міра дуги, на яку спирається вписаний кут дорівнює 140°, то величина кута також 140°. (Ні)
9. Величина центрального кута удвічі більша за величину кута, що спирається на ту саму дугу кола. (Так)
10.  Величина вписаного кута дорівнює двом центральним кутам, що спираються на одну і ту ж дугу кола. (Ні)
11.  У колі проведемо два радіуси. Якщо один з утворених центральних кутів у 3 рази більше другого, то їх величини будуть 90° і 270°. (Так)
12.  Величина вписаного кута 70°, а величина відповідної йому дуги 35°. (Ні)

 

                                                           

VII.  Домашнє завдання.

§1 п.9, вправа 291, 295, 301.