Кейс "Систематизація та поглиблення знань з курсу алгебри ", 7 клас
Завдання допоможуть учителям організувати підсумкове повторення з поглибленням курсу математики сьомого класу, а також їх можна застосовувати для індивідуальної роботи з учнями при підготовці до олімпіад.
1
7 клас. Алгебра (поглиблене) Акимова А.Л.
НВК «гімназія-школа» № 1
Систематизація
та поглиблення знань з курсу алгебри
7 клас
Підготувала:
Акимова Алла Леонідівна
Маріуполь, 2018 р
Завдання допоможуть учителям організувати підсумкове повторення з поглибленням курсу математики сьомого класу, а також їх можна застосовувати для індивідуальної роботи з учнями при підготовці до олімпіад.
Тема : Числові вирази.
1.Знайдіть значення виразу:
a)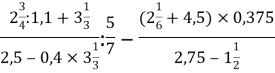 ;
;
б)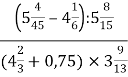 ×34
×34![]() +
+![]() +
+![]() ;
;
2.
а)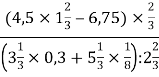 +
+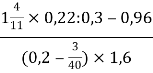 ;
;
б)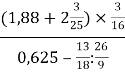 +
+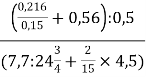 ;
;
3.Скільки відсотків складає число А від числа В, якщо:
а) А= ;
;
В=(16![]() ;
;
б) А=(2:3![]() (3
(3![]() ):
):![]() (2
(2![]() )×
)×![]() ;
;
В= .
.
4. а) Знайдіть ![]()
a=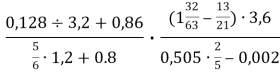 ;
;
б) Знайдіть число, ![]()
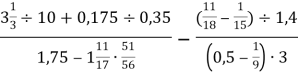 ;
;
5. Знайдіть значення змінної x із пропорції:
а) 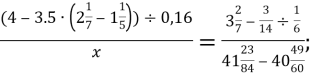
б)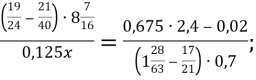
6. а) На скільки відсотків в значення змінної x, яке можна знайти з пропорції
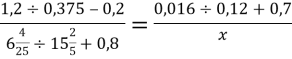 , менше за значення виразу
, менше за значення виразу ![]()
б) Знайдіть відношення ![]()
![]()
![]()
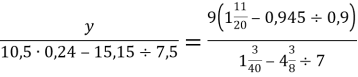
7. Знайдіть значення числових виразів:
а) ![]() ;
;
б)![]() ;
;
8. а)![]()
б)![]()
9.а)(1-![]() )(1-
)(1- ![]() )(1-
)(1- ![]() )…..(1-
)…..(1- ![]() );
);
б)(1- ![]() )(1-
)(1- ![]() )(1-
)(1- ![]() )…..(1-
)…..(1- ![]() ).
).
10.а)3(22+1)(24+1)(28+1)(216+1)(232+1)-2568;
б)8(32+1)(34+1)(38+1)(316+1)-818.
11.а)1+2+22+23+…..+212;
б)1+3+32+33+…..+39.
12.а)![]() -
- ![]() ;
;
б)![]() +
+ ![]() .
.
13.а)1997×2004×2011-2003(2005×2004+1)+49×2004;
б)156×161×166-159(161×163-20).
14.а)20005-19992(20003+2×20002+3×2000+4);
б)20044-2003×2005(20044+1).
15.а)1+ ![]() +
+ ![]() +
+ ![]() +…..
+….. ![]() +
+ ![]() ;
;
б)1-![]() +
+ ![]() -
- ![]() + ….. -
+ ….. -![]() +
+ ![]() -
- ![]() .
.
16.а)![]() -
- ![]() ;
;
б)![]() -
- ![]() .
.
17.а)20042004×200720072007-20072007×200420042004;
б)198198198×205205205205-205205205×198198198198.
18.(![]() +
+ ![]() )(
)(![]() -
- ![]() ).
).
Тема: Степінь з цілим невід’ємним показником
Знайдіть значення виразів:
1. а ) ![]()
б) –(-![]() : ( - (-
: ( - (-![]() : (-(-(-
: (-(-(-![]() ;
;
2. а) (-![]()
б) 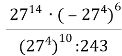 +
+ 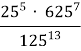 ;
;
3. а)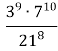
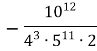 +
+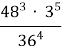 ;
;
б) 
4.а) (![]() ;
;
б) –(-![]()
5.а) (![]() де n є N;
де n є N;
б) (![]()
6.а)![]() ;
;
б) ![]()
7. а) 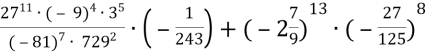 + (
+ (![]() ;
;
б) 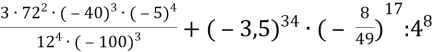
Приведить одночлени до стандартного вигляду:
8.а) ![]() ;
;
б) ![]() ;
;
9. а) ![]() ;
;
б) ![]() ;
;
10. a) ![]()
![]() ;
;
б) ![]() ;
;
Якою цифрою закінчується число:
11. а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
д) ![]()
Тема: «Цілі раціональні вирази»
Подайте вирази у вигляді многочлена:
-
А)
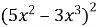 ; б)
; б) 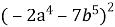 ; в)
; в) 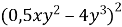 ;
;
Г) ![]() ; д)
; д) ![]() ; е)
; е)![]() ; ё)
; ё) ![]() ; ж)
; ж) ![]() ;
;
З) ![]() ;
;
и) ![]() ;
;
к) ![]() л)
л) ![]() ;
;
М) ![]() ; н)
; н) ![]() ;
;
О) ![]() ;
;
П) ![]() ;
;
Р) ![]()
С) ![]() ;
;
Т) ![]() ;
;
У) ![]() ;
;
2. а) ![]()
Б) ![]()
3. a) ![]()
б) 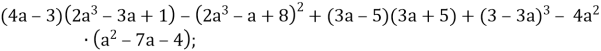
4. а) ![]()
Б) ![]()
Знайдіть значення виразу:
5. а) ![]() (
(![]() при
при
![]()
Б) 4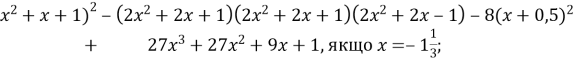
6. a) ![]()
Б) ![]() якщо
якщо ![]()
7. a) 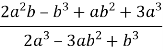 , якщо число а складає 40% числа b.
, якщо число а складає 40% числа b.
Б) 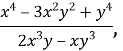 якщо число Y на 50% більше за число X.
якщо число Y на 50% більше за число X.
8. a) ![]() якщо
якщо ![]()
Б)![]() якщо
якщо ![]()
В) ![]() якщо
якщо ![]()
Г) ![]() якщо
якщо ![]()
9. Знайдіть найменше значення многочлена:
А) ![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г) ![]() д)
д) ![]() ; е)
; е)![]() ;
;
ж)![]() ; з)
; з) ![]() ;
;
10. Знайдіть найбільше значення многочлена:
А)![]() ; б)
; б)![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ;
;
11. Доведіть, що вирази набувають тільки додатних значень при будь-яких значеннях змінних:
А) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ;
;
д) ![]() ;
;
е) ![]() ;
;
12. Доведіть, що вирази набувають тільки від’ємних значень змінних:
А)![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ;
;
д) ![]() ; е)
; е) ![]() ;
;
13. Доведіть тотожність:
А) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) a2 – ((a –1)(a + 1)(a2 + a + 1) + (2 – a2)2 – a2(2a + 1) + 2a) : (2a2 – a – 3) = 1
14. Доведіть умовні тотожності:
a) Дано: x + y + z = 0, x2 + y2 + z2 = 1. Доведіть, що x4 + y4 + z4 = 0,5.
б) Дано: x + y + z = 0. Доведіть, що (x2 + y2 z2)2 = 2(x4 + y4 + z4).
в) Дано: x2 + y2 + 2z2 + 2t2 = 2xz + 2tz + 2yz. Доведіть, що x = y = z = t.
г) Дано: a + c = 2b, 2bd = bc + dc. Доведіть, що ad = bc;
15. Розкладіть многочлени на множники:
a) x2 – x – y2 – y; б) a2 – b2 – a – b; в) 4m2 – 2m + n – n2;
г) x2 – 2xc + c2 - d2; д) a2 + b2 – c2 + 2ab; е) p2 – x2 + 6x – 9;
ё) x2 – a2 – 10a – 25; і) 9 – c2 + a2 -6a; к) b2 – c2 -8b + 16;
л) bx2 + 2b2 – b3 - 2x2; м) x3 – 3y2 + 3x2 – xy2; н) 9( a + 1)2 – 1;
о) ( 7x – 4)2 – ( 2x + 1)2; п) 4 – 25( x – 3)2; р) 49( y – 4)2 – 9( y + 2)2;
с) 2( x – y)2 + 3( x2 – y2); т) 5a2 – 5 – 4( a + 1)2; у) 36 – b2 – c2 + 2bc;
ф) b2c2 – 4bc – b 2– c2 + 1; х) x3 – y3 – 5x( x2 + xy +y2); ц) p2 – 2p2 + 2p – 1;
ч) a2 – 4a2 + 20a – 125;
16. Розкладіть многочлен на множники:
1) x3 + y3 + 2x2 +2y2 – 2xy; 2) a4 + ab3 – a3b – b4; 3) a3 – b3 + 3a2 + 3ab + 3b2;
4) x4 + x3y – xy3 – y4; 5) ( 2a + 3b)3 – 18ab( 2a + 3b); 6) x4 – x2 – 2x – 1;
7) a5 – a2 – a – 1; 8) a128 – b128; 9) x4 – ( 1 + ab)x2 + ab;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() 15)
15)![]() 16)
16)![]() 17)
17) ![]() 18)
18)![]() ; 19)
; 19) ![]() 20)
20)![]()
17. Розкладіть многочлен на множники методом перегрупування:
1) ![]()
2)![]()
3)![]() ;
;
4) ![]()
5)![]()
6) ![]()
7) ![]()
8)![]()
9)![]()
10) ![]()
18. Розкладіть многочлен на множники зведенням до різниці квадратів:
![]() 2)
2)![]() 3)
3) ![]()
4) ![]() 5)
5)![]() 6)
6) ![]()
7)![]() ; 8) 4
; 8) 4![]() 9)
9) ![]()
10) ![]() ; 11)
; 11) ![]() 12)
12) ![]()
13) 4![]() 14) 25
14) 25![]()
19. Розкладіть на множники квадратні тричлени:
1)![]() 2)
2) ![]() 3)
3) ![]()
4) ![]() 5)
5) ![]() 6)
6) ![]()
7) ![]() 8)
8)![]() 9)
9) ![]()
Тема: «Рівняння»
- Розв’язати рівняння:
А) ![]() ;
;
Б) ![]()
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() ; е)
; е) ![]() ;
;
Ж) ![]() ;
;
З) ![]()
І) ![]() ;
;
К) ![]() ;
;
Л) ![]() ;
;
М) ![]() ;
;
Н) ![]() ;
;
О) 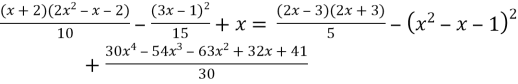 ;
;
2. 1) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ;
;
10) ![]() ; 11)
; 11) ![]() ;
;
12) ![]() ;
;
13) ![]() ;
;
14) ![]() ;
;
3. а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г)![]() ;
;
д) ![]()
4. Знайдіть пари чисел (x;y), які задовільняють рівняння:
А) ![]() б)
б) ![]() ; в)
; в)![]() г)
г)![]() ;
;
д) ![]() е)
е) ![]() ;
;
ж) ![]() ; з)
; з)![]() ;
;
і) ![]() ї)
ї)![]()


про публікацію авторської розробки
Додати розробку
