Позакласний виховний захід з математики на тему: «КОНКУРС ЮНИХ МАТЕМАТИКІВ»

Позакласний виховний захід з математики на тему: «КОНКУРС

ЮНИХ МАТЕМАТИКІВ»

Мета: навчальна: заохочувати учнів до вивчення матема­тики, активізувати й стимулювати розумову і пізна­вальну діяльність учнів;

          розвивальна: розвивати увагу, логічне мислення;

          виховна: виховувати працелюбність, акуратність.

Тип проведення: математична гра.

Обладнання. Вислови про математику, кросвор­ди, картки із завданням,

                       математичні малюнки, секундомір.

Література:

1.     Бевз Г.П. Конкурс юних математиків // Математика в школі. – 2008. - №16, - с. 6-8.
2.     Мерзляк А. Т., Болонський В.Б., Якір М.С. Алгебра: Підручник для 10 класу. –К.: Освіта – 2008. – 389с.

План

1.     Вступна частина.
2.     Основна частина (Проведення конкурсів).
3.     Заключна частина (Підсумки).

І. Вступна частина.

Учитель. Шановні учні! Багато важливих питань математики, зокрема й теоретичних, навіть входили в науку в формі цікавих задач, ігор та головоломок. Тож сьогодні ми з вами через гру будемо пізнавати цей цікавий світ, а знаряддями нашої гри будуть розум, кмітливість, увага.

Увага! Увага! Розпочинаємо наш математичний конкурс. Запрошуємо юних любителів математики! (Під музику входять команди.) Учнів класу об'єднано в три команди.

ІІ. Основна частина.

ХІД ГРИ

I. Привітання команд.

II. Конкурси.

«КРОСВОРД»

Командам пропонується математичний кросворд. Протягом 3 хв вони повинні дати найбільше від­повідей. Правильна відповідь оцінюється 1 балом.

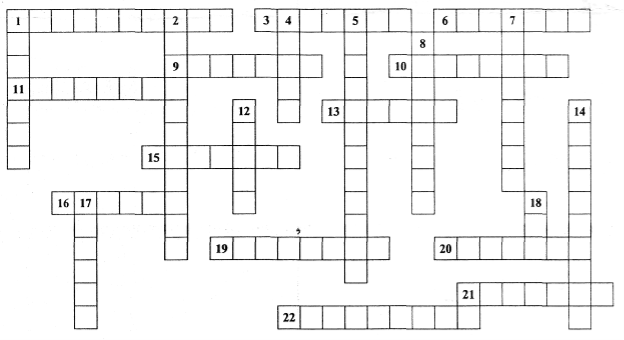
По горизонталі:

1. Два тотожно рівні вирази, сполучені знаком рівності. 3. Другий степінь числа. 6. Многочлен, який містить два доданки. 9. Наука про рівняння. 10. Два вирази, сполучені знаком рівності. 11. Добуток чисел, змінних та їх степенів. 13. Значення невідомого, при якому рівняння перетворюється на правильну рівність. 15. Многочлен, який містить три доданки. 16. Перетворення виразу, при якому даний вираз замінюється тотожним йому. 19. Число, яке показує, до якого степеня підноситься осно­ва. 20. Члени многочлена, що відрізняються тільки коефіцієнтами. 21. Добуток кількох рівних множ­ників. 22. Сума кількох одночленів.

По вертикалі:

1. Два вирази, відповідні значення яких рівні при будь-яких значеннях змінних. 2. Вигляд одночлена, що містить тільки один числовий множник, а кожна змінна входить тільки до одного множника. 4. За­пис, складений з чисел і букв, сполучених зна­ками дій. 5. Вираз, що не містить ніяких інших дій, крім додавання, віднімання, множення, під­несення до степеня і ділення. 7. Вираз, що містить лише числа. 8. Рівність, що містить невідоме. 12. Ра­ціональний вираз, який не містить ділення на ви­раз із змінною. 14. Числовий множник одночлена, записаного в стандартному вигляді. 17. Число, яке підносять до степеня. 18. Третій степінь числа.

Відповідь.

По горизонталі: 1. Тотожність. 3. Квадрат. 6. Двочлен. 9. Алгебра. 10. Рівність. 11. Одночлен. 13. Корінь. 15. Тричлен. 16. Тотожне. 19. Показник. 20. Подібні. 21. Степінь. 22. Многочлен.

По вертикалі: 1. Тотожні. 2. Стандартний. 4. Ви­раз. 5. Раціональний. 7. Числовий. 8. Рівняння. 12. Цілий. 14. Коефіцієнт. 17. Основа. 18. Куб.

«ХТО ШВИДШЕ?»

Командам у друкованому вигляді роздаються завдання. Яка команда швидше виконала та отримує 3 бали.

1.     Батько все своє майно, 17 верблюдiв, заповiдав синам, причому старший мав одержати половину, середнiй — третину а найменший — дев’яту частину. Пiсля смертi батька сини не знали, що робити, бо 17 не дiлилося без остачi нi на 2, нi на 3, нi на 9. Довго сперечалися брати, аж тут пiд’їхав до них на верблюдi мудрець. Довiдався про суперечку i дав братам мудру пораду, яка й допомогла роздiлити майно так, як заповiв батько. Що то була за порада?

Мiркування: Мудрець вiддав братам свого верблюда, верблюдiв стало 18. Тодi їх подiлили вiдповiдно до батькового заповiту. Старший одержав 9, середнiй 6, молодший 2. Усього 17. А мудрець забрав свого верблюда й поїхав далi.

2.     Висота дуба 20м. За день мурашка пiднiмається по ньому на 5м вверх, а за нiч спускається на 4м вниз. За скiльки днiв мурашка доповзе до вершини дуба?

Мiркування: За 16 днiв. За кожнi з перших 15 дiб мурашка пiднiмався на 1м. Отже, за 15 дiб вiн пiднявся вверх на 15м. А за 16-й день мурашка пiднiметься ще на 5м i досягне вершини.

3.     Три недiлi одного місяця припадають на непарнi дати. Причому одна з них — на 17 число. Скiльки днів у цьому мiсяцi?

Мiркування: Якщо одна недiля 17-го числа, то наступна — 24-го. До 17-го числа неділi були 10-го i 3-го. Таким чином, з 3-го до 24-го недiлi припадають на 2 непарнi дати, а тому третя недiля, яка припадає на непарну дату, буде 31-го числа. Отже, у мiсяцi 31 день.

4.     Який зараз день і котра година, якщо вiд дев’ятої години суботнього вечора хвилинна стрiлка годинника зробила рiвно 40 обертiв?

Мiркування: Кожний оберт хвилинна стрiлка робить за одну годину, а 40 обертiв — 40 годин. Через добу (24 години) була недiля, 9 годин вечора, а ще через 3 години — 12 годин ночi, пiсля чого почався понеділок. Таким чином, до дванадцятої години ночi пройшло 27 годин (24 + 3 = 27), залишилося 13 годин (40 — 27 = 13) на понеділок. Отже, маємо 1 годину дня, понеділок.

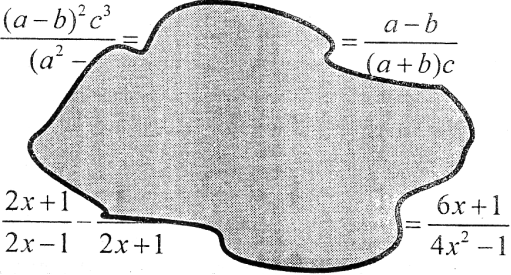
 «ВИТЕРТІ ЗАПИСИ»

Команди працюють у повному складі. Потрібно відновити записи на дошці. Час виконання — 10 хв. Правильна відповідь до кожного із записів оцінюється 5 балами.

 

«КАПІТАН»

Грають капітани команд. Правильна відповідь на кожне запитання оцінюється 1 балом.

Запитання для капітана І команди

1. Наука про властивості геометричних фігур. (Геометрія.)

2. Твердження, що потребує доведення. (Теорема.)

3. Що в геометрії позначають однією великою латинською літерою? (Точку.)

4. Сума одночленів. (Многочлен.)

5. Фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно сполучають ці точки і не лежать на одній прямій. (Чотирикутник.)

6. Сума кутів трикутника. (180°.)

7. Паралелограм, у якого всі сторони рівні. (Ромб.)

Запитання для капітана II команди

1. Промінь, який виходить з вершини кута, проходить між його сторонами і ділить кут навпіл. (Бісектриса.)

2. Твердження, яке не потребує доведення. (Аксіома.)

3. Кут, суміжний з прямим, дорівнює .... (90°.)

4. Значення змінної, при яких дріб має зміст. (Допустимі значення змінної.)

5. Відрізок, що сполучає дві протилежні вершини многокутника. (Діагональ.)

6. Чотирикутник, у якого протилежні сторони паралельні. (Паралелограм.)

7. Чотирикутник, у якого тільки дві сторони паралельні. (Трапеція.)

Запитання для капітана III команди

1. Прямі, які перетинаються під прямим кутом. (Перпендикулярні.)

2. Геометрична фігура, яка складається з точки і двох променів, що виходять з цієї точки. (Кут.)

3. Рівність з однією змінною. (Рівняння.)

4. Добуток однакових множників. (Степінь.)

5. Сума довжин усіх сторін фігури. (Периметр.)

6. Сума кутів чотирикутника. (360°.)

7. Прямокутник, у якого всі сторони рівні. (Квадрат.)

III. Заключна частина.

IV. Підбиття підсумків гри. Нагородження грамотами команд.