Кейс-урок "У світі призм"

ПРОФЕСІЙНО-ТЕХНІЧНЕ УЧИЛИЩЕ №36

смт НОВГОРОДКА

Номінація : STEM-урок

Тема: Кейс-урок « У світі призм»

Підготувала : викладач

 математики та фізики

 Шкварько Євгенія Іванівна

2024

КЕЙС-УРОК «У СВІТІ ПРИЗМ»

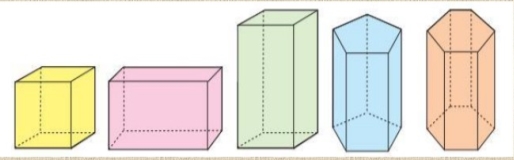
АКТУАЛЬНІСТЬ КЕЙСУ. Один з найпростіших многогранників – призма. Вона має різні види – пряма призма, паралелепіпед, куб, правильна призма. Не зважаючи на свою простоту,  вона відіграє важливу роль у нашому житті. На превеликий жаль теми про всі властивості і застосування даного геометричного тіла розкидані по різних предметах і самостійно учням досить складно об’єднати всі отримані знання в цілісне уявлення про дану фігуру. Є дуже важливим показати учням, як знання про властивості даної фігури використовуються у різних галузях нашого повсякденного життя, як знання з геометрії пояснюють різні процеси у фізиці, біології, інженерії, медицині та застосовуються в літературі.

Розділ: STEAM

Рівень:  для учнів ІІ курсу

Тема: Призма

Мета: Формувати поняття призми та її елементів;

Розвивати пізнавальну активність, розширювати кругозір учнів, життєві компетенції;

Виховувати наполегливість, самостійність, старанність у навчанні;

Підвищити  мотивацію до вивчення теми «Призма», розглянути призму не тільки як геометричну фігуру, а й різні аспекти її використання;

Усвідомити  цінність  знань для життя.

Отримані результати і напрацьовані компетенції:

      вміння швидко відшукати необхідну інформацію за темою;

      вміння креативно використовувати отриману інформацію з практичною метою;

      засвоєння конкретних знань з геометрії, алгебри, фізики, біології та інших розділів (наведені в розгортці);

      вміння «конструювати» отриманні знання на основі отриманих відомостей;

      розвиток інтелектуальних та комунікативних навичок.

Вступ.

ШІ згенерував зображення у яких закодовано прислів’я.

-          Погляньте на них, та назвіть ці прислів’я

-          Чи згодні ви з ШІ?

-          Можливо зображення повинне бути іншим?

-          Отримуючи нові знання, ми повинні  критично відноситися до всієї інформації.

Сьогодні на уроці ми застосуємо відомий у світі  «кейс – метод». Напередодні уроку кожен учень отримав завдання ознайомитися з певним набором інформації, що входить до складу узятого «кейсу». Використовуючи цю інформацію та знання, які ви отримали на попередніх уроках вам необхідно буде виконати завдання з метою розв’язання конкретних життєвих ситуацій. Отже, ми перенесемось у цікавий світ математики, а точніше у світ призм. Ми зрозуміємо, що математичні поняття, геометричні фігури, їх властивості широко застосовуються не лише у математиці а й у різних галузях нашого повсякденного життя.

РОЗГОРТКА КЕЙСУ ЗА НАПРЯМКАМИ:

    Історія

    Математика

    Фізика

    Оптична інженерія

    Медицина

    Біологія

    Література

    Архітектура

    Архітектор по імені природа

ІСТОРІЯ

В пам'ятниках вавілонської і древньоєгипетскої архітектури зустрічаються такі геометричні фігури, як куб, паралелепіпед, призма. Найважливішою задачею єгипетської і вавілонської геометрії було визначення об'єму різних просторових фігур. Ця задача відповідала необхідності будувати будинки, палаци, храми і інші споруди.

       Частина геометрії, в якій вивчаються властивості куба, призми, паралелепіпеда і інших геометричних тіл і просторових фігур, здавна називається стереометрією; Слово це грецького походження ( "стереос" - просторовий, "метрео" - вимірюю) і зустрічається ще у славнозвісного древньогрецького філософа Арістотеля.

Стереометрія виникла пізніше, ніж планіметрія. Евклід дає наступне визначення призми: "Призма є тілесна (тобто просторова) фігура, укладена між площинами, з яких дві протилежні рівні і паралельні, інші ж - паралелограми". Тут, як і в багатьох інших місцях, Евклід вживає термін "площина" не в значенні безмежно продовженої площини, а в значенні обмеженої її частини, грані, подібно тому як "пряма" означає у нього і відрізок прямий.

Термін "призма" грецького походження і буквально означає "відпиляне" (тіло).

Термін "паралелепіпедальне тіло" зустрічається уперше у Евкліда і означає дослівно "паралеле-площинне тіло". Грецьке слово "кубос" вживається Евклідом в тому ж значенні, що і наше слово "куб"

Визначення паралелепіпеда. Призма, основа якої - паралелограм, називається паралелепіпедом.

       У відповідності з визначенням паралелепіпед - це чотирикутна призма, всі грані якої - паралелограми. Паралелепіпеди, як і призми, можуть бути прямими та похилими.

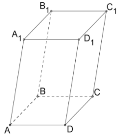             Прямий паралелепіпед, основою якого служить прямокутник, називають прямокутним  паралелепіпедом. У прямокутного паралелепіпеда всі грані - прямокутники. Моделями прямокутного паралелепіпеда служать класна кімната, цегла, сірникова коробка.

https://www.miyklas.com.ua/p/geometria/10-klas/paralelnist-priamikh-i-ploshchin-u-prostotri-14771/tetraedr-i-paralelepiped-14778/re-3873212a-91f2-4a9d-afa3-dcf2a8925a5f

Об'єми зернових комор і інших споруд у вигляді кубів, призм і циліндрів єгиптяни і вавилоняни, китайці і індійці обчислювали шляхом множення площі основи на висоту. Однак древньому Сходу були відомі в основному тільки окремі правила, знайдені дослідним шляхом, якими користувалися для знаходження об'ємів для площ фігур. У більш пізній час, коли геометрія сформувалася як наука, був знайдений загальний підхід до обчислення об'ємів многогранників.

ЗАВДАННЯ.

Фермер має споруду для зберігання сіна у формі призми з довжиною 10 м, шириною 5 м, і висотою 3м. Фермер хоче знати з якої площі можна зібрати сіно для зберігання у  цьому сіннику. (Нам відомо, що сіно стискається у приблизно в однорідну масу, можемо припустити, що його густина приблизно однакова. Зазвичай густина сіна коливається від 100 до 200 кг/м³.)

МАТЕМАТИКА

Призма — це многогранник, дві грані якого є рівними многокутниками, що знаходяться в паралельних площинах, а інші грані — паралелограми.

Грані, які знаходяться в паралельних площинах, називаються основами призми, а інші грані — бічними гранями призми.
Залежно від основи призми бувають: 

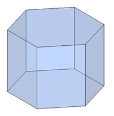
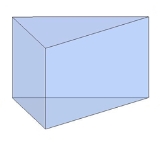 трикутними         шестикутними та ін.

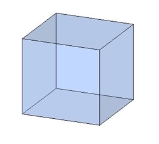
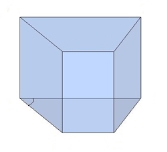
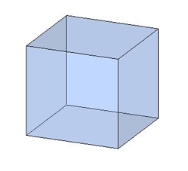
чотирикутними                                                        

Призма з бічними ребрами, перпендикулярними її основам, називається прямою призмою, як у попередніх малюнках.

Пряма призма називається правильною, якщо її основи — правильні многокутники.

Призма, бічні ребра якої не перпендикулярні основам, називається похилою призмою.

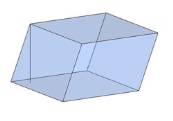
Відстань між основами призми називається висотою призми.

Зверни увагу!

Висота прямої призми збігається з боковим ребром.

Висота похилої призми — це перпендикуляр, проведений між основами призми. Часто перпендикуляр проводять з однієї з вершин верхньої основи.

Зверни увагу!

Без додаткових умов неможливо визначити, в яку точку проектується висота похилої призми.

 Паралелепіпед — це чотирикутна призма, всі грані якої є паралелограмами.

Паралелепіпеди — особлива група призм.
Як видно на даних малюнках, об'ємні малюнки прямих паралелепіпедів практично не відрізняються.
У паралелепіпеда 12 ребер і 6 граней.

Види паралелепіпедів

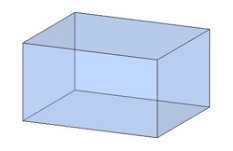
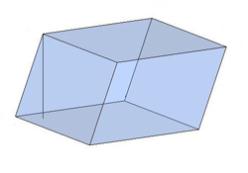
Похилий                                                    Прямий  

Види прямих паралелепіпедів

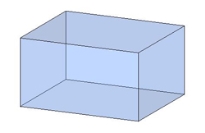
Прямий паралелепіпед, основа — паралелограм.  

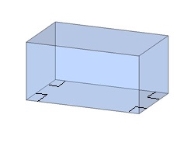Прямокутний паралелепіпед, основа — прямокутник.

Спеціальні випадки прямокутного паралелепіпеда

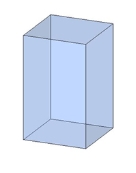
Правильна чотирикутна призма, основа — квадрат, висота призми не обов'язково дорівнює стороні основи.

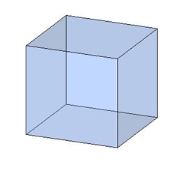
Куб, всі ребра куба рівні, всі грані — квадрати.

Діагональ призми  — це відрізок, який з'єднує дві вершини, які не належать одній грані.

Діагональ не існує тільки у трикутної призми.

Якщо діагоналі основи прямої призми рівні, тоді діагоналі самої призми теж рівні.

Наприклад, у куба, правильної чотирикутної призми, прямокутного паралелепіпеда діагоналі рівні DF=EC, оскільки DB=CA, 

а у паралелепіпеда, в основі якого знаходиться паралелограм, діагоналі тільки попарно рівні DF≠EC, оскільки DB≠CA

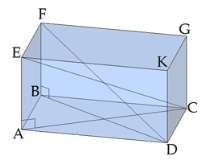
Діагональний переріз призми — це переріз площиною, що проходить через два бічних ребра, які не належать одній грані.

Кожний діагональний переріз містить дві діагоналі призми.

Діагональний переріз прямої призми є прямокутником.

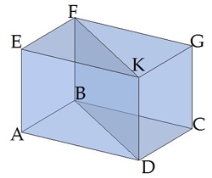
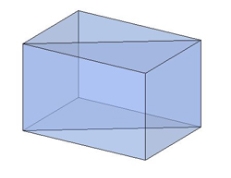Діагональний переріз похилої призми — паралелограм.

Зверни увагу!

У правильного шестикутника діагоналі бувають двох видів — короткі і довгі.
У зв'язку з цим існує два види діагональних перерізів шестикутної призми:

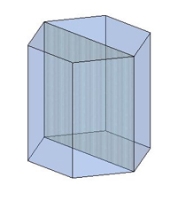
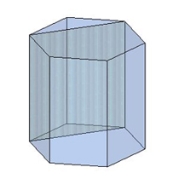
Приклад:

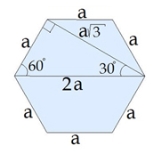
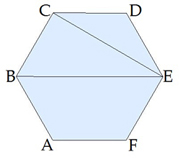
Як знайти діагоналі правильного шестикутника, якщо відома довжина його сторони?
CE — одна з коротких діагоналей шестикутника, BE — одна з довгих діагоналей.
Враховуючи те, що кути правильного шестикутника дорівнюють 120 градусів,
легко знайти прямокутний трикутник, в якому є кут 30 градусів, й використати співвідношення в цьому трикутнику.

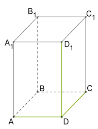
Пряма призма, основою якої є прямокутник, називається прямокутним паралелепіпедом.

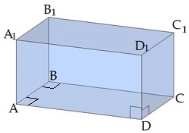Довжини трьох ребер, що мають спільну вершину, називаються вимірами прямокутного паралелепіпеда.

Наприклад, три виміри — це довжини трьох ребер DA, DC, DD₁.

Квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірів: 

D²=a²+b²+c²

де a,b,c — виміри прямокутного паралелепіпеда, тобто, його довжина, ширина і висота.

На малюнку: DB₁₂=DA₂+DC₂+DD₁₂

Зверни увагу!

У прямокутного паралелепіпеда всі діагоналі рівні:

DB₁=CA₁=AC₁=BD₁

Приклад:

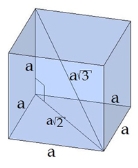Формула діагоналей куба

Оскільки у куба всі виміри рівні, позначаємо їх за a, тоді

D²=a²+a²+a²=3a².

Спрощуємо і отримуємо формулу діагоналі куба:

D=a√3

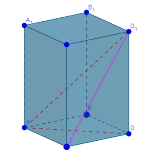
        - Подивіться уважно  на цей многогранник і скажіть, який вид призми тут    зображено.

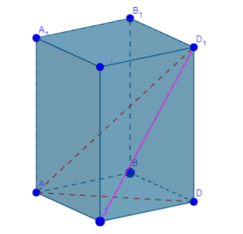
-  Назвіть бічну грань , яким многокутником є ця грань?

-  Назвіть діагональ призми, діагональ бічної грані, кут між діагоналлю і площиною основи, кут між діагоналлю бічної грані і площиною основи.

-  Чи може цей многогранник бути зображенням правильної чотирикутної призми?

-  Назвіть вид цього многогранника?

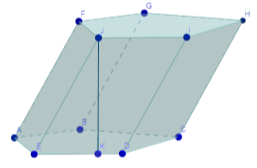-  Яким видом многокутника є його бічна грань?

-  Назвіть висоту, бічне ребро цього многогранника. Чи може цей многогранник бути зображенням правильної  призми?

В даній ментальній карті зібрано всі властивості призми. Згадайте їх.

https://www.miyklas.com.ua/p/geometria/11-klas/mnogogranniki-15488/poniattia-mnogogrannika-prizma-15489/re-89bb0a96-d7c4-4d24-918c-91f9e847386e

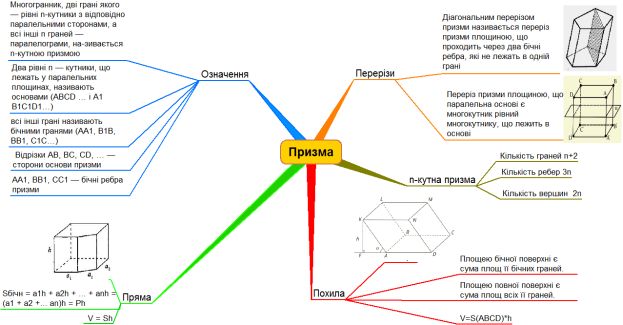
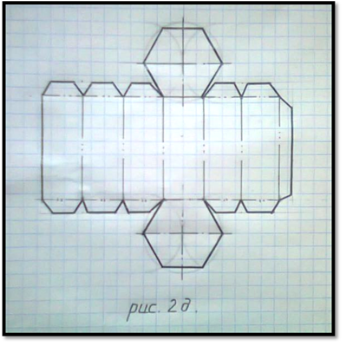ЗАВДАННЯ.

За розгорткою, зображеною на рисунку, зробіть модель шестикутної призми. Виконайте необхідні виміри, обчисліть  площу бічної поверхні, повної поверхні та об’єм призми.

 (Модель виконайте у масштабі 1:3)

https://jak.bono.odessa.ua/articles/pobudova-rozgortki-shestikutnoi-prizmi.php

ФІЗИКА

У 1665-1666 році юний Ісаак Ньютон, тільки-но закінчивши кембріджський Трініті-коледж, бився над проблемою удосконалення телескопа. Головним недоліком тодішніх телескопів було райдужне забарвлення країв зображень. Намагаючись зрозуміти природу цього явища, Ньютон використав скляну призму. 

Він закрив вікна щільними віконницями, в яких  зробив невеликий отвір. Пучок променів, що проходив через цей отвір, він направив на протилежну стіну, поставивши на його шляху призму. Світло, пройшовши через призму, потрапляло на екран на стіні у вигляді різнобарвної смуги, подібної до веселки. Ньютон пізніше назвав її спектром. Він провів кілька серій подібних дослідів, які навели його на думку, що всі кольори є у світлі спочатку, і саме призма розкладає їх на спектр.

Це відбувається за рахунок того, що світло, яке щойно проходило через повітря, потрапляючи на грань скляної призми, заломлюється. Таке заломлення світла відбувається при потраплянні його на кордон будь-яких двох середовищ («повітря-скло», «повітря-вода», тощо). Це добре видно, якщо подивитися на ложечку в склянці з водою. Вона теж виглядає начебто переламаною.

Так само переломлюються промені світла в призмі. А кут, під яким вони переломлюються, залежить від довжини хвилі. А ще — саме від довжини хвилі залежить колір. Виходить, що промені з різною довжиною хвилі заломлюються під різними кутами. І розкладаються на спектр. 

Саме цей феномен зображено на знаменитому альбомі групи «Пінк Флойд» «Темна сторона місяця».

Так, до речі, і з'являється веселка. 

Після дощу в повітрі висять мільйони маленьких крапель, кожна з яких є своєрідною маленькою призмою, що переломлює промені сонця і розкладає їх на спектр. Це явище і називається дисперсією світла.

«Harpe de Lumière», фотография Georges Noblet

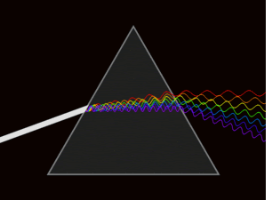Дисперсійні призми

Дисперсійні призми використовуються в спектральних приладах для просторового розділення випромінювань різних довжин хвиль.

Проста тригранна призма

Призма Броунінга-Рузерфорда

Дисперсійна призма Аббе

Призма Амічі (призма прямого зору)

Відбивальні призми

Відбивальні призми використовують для зміни ходу променів, зміни напряму оптичної осі, зміни ліній візування, для зменшення габаритних розмірів приладів. Класифікують відбивальні призми за кількома ознаками:

кількістю відбивань в призмі;

наявністю або відсутністю «даху»;

характером конструкції призми;

кутом злому оптичної осі.

Також, окрему нішу серед відбиваючих призм займають призми, які складаються з кількох частин, розділених повітряними проміжками. Деякі широко використовуванні призми отримали власні імена:

Пентапризма;

Призма Порро;

Призма Аббе-Порро;

Призма Аббе;

Призма Пехана-Шмідта;

Призма Дове;

Призми з «дахом»;

Дихроїдна призма.

Назва призми позначається двома або трьома літерами і числом, записаним через дефіс. Перша літера означає кількість відбиваючих граней в призмі:

А — одна;

Б — дві;

В — три і т. д.

«Дах», умовно, вважають як одну грань і для неї ставлять індекс «к» після першої літери (наприклад, Ак, Бк). Друга буква вказує на характер конструкції:

Р — рівнобедренна;

С — ромбічна;

П — пентапризма;

У — напівпентапризма;

М — далекомірна;

Л — призма Лемана.

Цифри, які записані через дефіс, вказують на кут злому оптичної осі. (0°,90°,180°). Наприклад, «ВкР-45°» — рівнобедренна призма з трьома відбивальними гранями і «дахом», з кутом злому 45°.

Складені призми вказуються за їхніми власними іменами і кутами злому осі. Наприклад, «А-0°» — Призма Аббе, «Бк-90°» — башмачна призма з «дахом», «К-0°» — призма-куб.

Поляризаційні призми

• Призма Ніколя
• Призма Волластона
• Призма Аренса
• Призма Глана-Фуко
• Призма Глазебрука
• Призма Рошона

ЗАВДАННЯ.

1.У якому з випадків а-г на рисунку правильно по­казано хід світлового променя, що зазнав заломлен­ня, падаючи з повітря на поверхню прозорого ма­теріалу?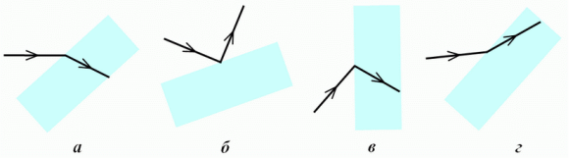

2.Чи можна створити плащ-невидимку, як у Гаррі Поттера?

ОПТИЧНА ІНЖЕНЕРІЯ

Оптична інженерія — область дослідження, яка фокусується на застосуванні оптики. Оптична техніка займається розробкою оптичних приладів, таких як лінзи, мікроскопи, телескопи та інше обладнання, яке використовує властивості світла за допомогою фізики та хімії.

Інженери-оптики використовують переваги оптики, одного з фундаментальних предметів фізики, і працюють у широкому діапазоні областей від медицини до автомобільної промисловості. Оптична інженерія, яка є однією з міждисциплінарних інженерних галузей, може працювати в будь-якій галузі, включаючи світло. Інженерам-оптикам необхідно мати знання в таких галузях, як математика, фізика, геометрія.

Властивість призми розкладати світло на спектри лежить в основі принципу роботи оптичних приладів.

Призми використовуються в оптичних системах для вигинання та фокусування світла, для зміни напрямку світла, розділення на кольори та інших цілей. Наприклад, в призматичних біноклях, телескопах, мікроскопах.

У біноклях призми використовуються для зміни напрямку світла, що дозволяє зображенню з обох об'єктивів потрапляти в обидві окуляри.

У телескопах призми використовуються для фокусування та збільшення зображення, а також для зміни напрямку світла у трубі телескопа.

У мікроскопах призми використовуються для фокусування світла на досліджуваному об'єкті та для створення збільшеного зображення.

У фото- та відеокамерах призми використовуються для направлення світла в об'єктив, фокусування та корекції зображення.

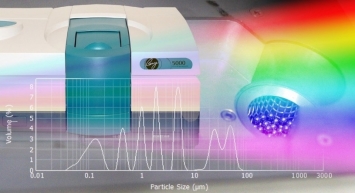Спектроскопія: Призми грають ключову роль в спектроскопії, де вони використовуються для розбиття світла на його складові кольори (спектр) та аналізу цього спектра. Ось деякі основні застосування призм в спектроскопії:

Дисперсія світла: Призма розбиває біле світло на спектральні компоненти (кольори) через явище дисперсії світла, де кожен колір відповідає певній довжині хвилі світла.

Спектральний аналіз: Призми використовуються для аналізу складу речовини за її спектральним відбиттям, поглинанням або розсіюванням світла. Це дозволяє визначати хімічний склад та фізичні властивості речовини.

Спектроскопічні прилади: Призми використовуються у спектроскопах для розбиття спектральних ліній на окремі компоненти для подальшого аналізу. Такі прилади дозволяють вивчати властивості атомів, молекул та інших об'єктів.

Визначення відстаней: У високоточних спектроскопічних методах, таких як астрофізична спектроскопія, призми використовуються для визначення відстаней до далеких об'єктів за спектральним зсувом їхніх спектрів.

Ультрафіолетова спектроскопія: У спектроскопії ультрафіолетового (УФ) діапазону призми використовуються для розбиття та аналізу УФ-випромінювання, що є важливим для досліджень у хімії, біології та фізиці.

Інтерференційні прилади: У деяких спектроскопічних методах, наприклад у фур'є-спектроскопії, призми використовуються для створення інтерференційних смуг, які дозволяють отримувати дуже високу роздільну здатність у спектрах.

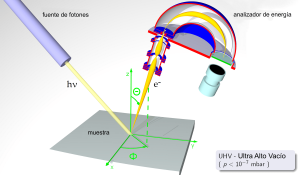Хімічна аналітика: У спектроскопії, фотометрії та інших методах аналізу призми використовуються для вимірювання властивостей речовин за їх взаємодією зі світлом.

Комунікації: У деяких типах оптичних волокон для передачі даних використовуються призми для збільшення ефективності передачі світлового сигналу.

Лазерна техніка: Призми використовуються в лазерних системах для вирівнювання, розсіювання та фокусування лазерного променя.

У лазерних приладах призми відіграють кілька важливих ролей:

Формування лазерного променя: Призми допомагають формувати лазерний промінь, зазвичай вирівнюючи його або концентруючи. Це важливо для забезпечення прямолінійності та інтенсивності променя.

Регулювання напрямку та фокусування: Призми використовуються для направлення лазерного променя у потрібному напрямку та для фокусування його на місці дії.

Розділення променя: Деякі призми використовуються для розділення лазерного променя на декілька променів, що може бути корисним для додаткових застосувань, наприклад, в області наукових досліджень.

Модифікація властивостей променя: Призми можуть бути використані для зміни поляризації, частоти або інших властивостей лазерного променя, що дозволяє отримувати потрібні для конкретних застосувань характеристики.

Захист оптичних елементів: Призми також можуть використовуватися для захисту інших оптичних елементів в лазерному пристрої, наприклад, від небажаного впливу пилу або інших домішок.

У загальному, призми у лазерних приладах використовуються для керування, формування та оптимізації роботи лазерного пристрою, що дозволяє досягти потрібних характеристик променя та підвищити ефективність його застосування.

Проекція: Призми використовуються у проекційних системах для розбиття та направлення світлового променя для створення зображень.

У проекційних апаратах призми використовуються для різних цілей, ось деякі з них:

Зміна напрямку світла: Призми використовуються для зміни напрямку світла у проекційних апаратах. Наприклад, вони можуть використовуватися для відбиття світла від джерела на екран або іншу поверхню.

Корекція зображення: Призми можуть використовуватися для корекції та підвищення якості зображення у проекційних апаратах. Наприклад, вони можуть використовуватися для корекції аберрацій та інших спотворень зображення.

Перетворення зображення: У деяких проекційних апаратах призми використовуються для перетворення зображення, наприклад, для збільшення або зменшення його розміру або для створення інших ефектів.

Розділення кольорів: У кольорових проекційних апаратах призми використовуються для розділення світла на складові кольори (червоний, зелений, синій) для подальшого комбінування їх для створення кольорового зображення на екрані.

Керування світлом: Призми можуть використовуватися для керування інтенсивністю світла, його розподілом або напрямком в проекційних апаратах.

Створення спеціальних ефектів: У деяких випадках призми використовуються для створення спеціальних ефектів у проекційних апаратах, таких як розсіювання світла або створення геометричних малюнків.

Це лише декілька прикладів застосування призм у проекційних апаратах. Вони дозволяють покращити якість зображення та забезпечити більш гнучке управління світлом у таких пристроях.

ЗАВДАННЯ

1.На скляну призму з кутом заломлення α=60° падає промінь світла. Визначте показник заломлення n, якщо при симетричному ході променя в призмі кут відхилення γ=40°. Для побудови ходу променя в призмі перегляньте відео https://www.youtube.com/watch?v=GXdbDBJnAuI

2. Перегляньте відео https://www.youtube.com/watch?v=sdfP2JuWN7g

Створіть саморобний спектроскоп.

МЕДИЦИНА

У медичній діагностиці призми використовуються для вивчення внутрішніх органів, а також для створення оптичних інструментів, які допомагають у хірургічних операціях.

Призми мають кілька важливих застосувань в медицині, особливо в оптиці та обладнанні для досліджень. Ось деякі з них:

Лікарські дослідження: Призми використовуються в медичних дослідженнях для аналізу складу тканин, вивчення морфології клітин, виявлення патологічних змін та інших діагностичних цілей.

Оптичні прилади: У медичній оптиці призми використовуються для створення оптичних систем, таких як мікроскопи, ендоскопи та інші обладнання для дослідження внутрішніх органів та тканин.

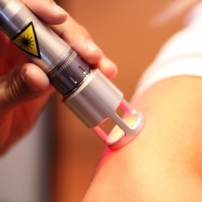Лазерна терапія: У лазерній медицині призми використовуються для управління шляхом лазерного променя та фокусування його на певній області для здійснення хірургічних або терапевтичних процедур.

Діагностика: Призми використовуються для створення різних типів діагностичних приладів, таких як спектроскопи, оптичні камери, системи зображення та інші, які допомагають у виявленні та діагностиці хвороб.

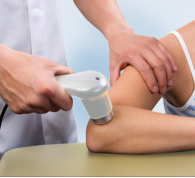Фізіотерапія: У фізіотерапії призми можуть використовуватися для створення спеціальних оптичних систем, що допомагають відновлювати функції м'язів та суглобів після травм або операцій.

Окуляри: Оптичні призми використовуються для корекції рефракції ока та лікування різних офтальмологічних захворювань, таких як страбізм, амбліопія та інші.

Призматичні окуляри: принцип дії та за яких очних захворювань потрібні

Закриваєте одне око, щоб не відчувати двоїння? Якщо ви відчуваєте симптоми, такі як головні болі, розмитий зір або важкість у фокусуванні, подвоєння обʼєктів це може бути ознакою того, що вам потрібні окуляри з призматичною корекцією.

Призматичні окуляри – це спеціальні окуляри з лінзами, які містять призми, що змінюють напрямок ходу світла. Вони можуть бути використані для різних медичних станів, де виникають проблеми із бінокулярним зором.

Як працюють призматичні окуляри?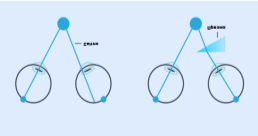 Призматичні окуляри працюють за допомогою спеціальних лінз з призмами, які змінюють напрямок світла, що проходить через них. Це допомагає вирівняти зорову вісь.

Для кого підходять?

•             Для тих, у кого двоїться в очах. Призматичні окуляри можуть бути призначені для людей, які мають проблеми що призводить до подвійного бачення (подвоєння зображення). Призми в окулярах допомагають зіставити зображення з обох очей, щоб уникнути подвоєного зображення.
•             Для людей з косоокістю. У деяких випадках призматичні окуляри можуть бути використані для корекції проблем коли окорухові мʼязи не працюють належним чином.
•             При діагнозі “форія” (або прихована косоокість). Людина може помітити форію сама. Наприклад, на фото або коли вона замислюється, очі відходять убік, як тільки з’являється об’єкт фіксації, тобто пацієнт перемикає увагу на когось або щось, очі стоять рівно.

* Призматичні окуляри призначаються при декомпенсованій форії.

Загалом, призматичні окуляри можуть бути важливим інструментом для корекції різних зорових проблем, але вони повинні бути призначені і підготовлені фахівцем, який проведе оцінку вашого зору та визначить необхідність використання призматичних окулярів.

Підбір призматичних окулярів є важливим процесом, оскільки вони використовуються для корекції проблем з бінокулярним зором, таких як страбізм або амбліопія. Цей процес зазвичай виконується окулістом або ортоптометром. Для визначення величини та орієнтації призми окуліст може використовувати різні методи та формули, в залежності від конкретного випадку. Одними з найпоширеніших є методи Маддокса та методи скрінінгу Френеля. Формула для обчислення величини та орієнтації призми може бути такою: