Повторення. Розв’язування задач на обчислення площ многокутників

Про матеріал

Урок з використанням елементів STEAM – освіти Завдання Протягом уроку учні зможуть: - повторити означення та властивості вивчених многокутників та формули обчислення їх площ; - закріпити уміння знаходити площі фігур; - закріпити уміння застосовувати формули для розв'язування прикладних задач; - поглибити свої знання цікавими фактами з життя; - удосконалювати вміння оцінювати свої знання, працювати в парах та в групах.

Перегляд файлу

Save the Date! STEAM Night | Technology News

Геометрія 11 клас

Розробила вчитель інформатики та математики Галак С.О.

2024

Тема: Повторення. Розв’язування задач на обчислення площ многокутників

Формування компетентностей:

предметна компетентність:

 навчальна: закріплення в учнів навичок розв’язування типових задач з теми «Площі многокутників», навичок застосування програмних засобів для спрощення розрахунків при розв’язанні задач; формування навичок використання вбудованих функцій табличного процесора; розвиток уважності, логічного та алгоритмічного мислення; виховання активності, самостійності, вміння працювати у групі, критично оцінювати свою роботу;

 розвивальна: розвивати інформаційну культуру учнів;

 виховна: виховувати інформаційну культуру, виховання уміння працювати в групі; формування позитивного ставлення до навчання.

ключові компетентності:

 спілкування державною мовою: формувати вміння висловлюватись та спілкуватися із використанням відповідної термінології;

 основні компетентності у природничих науках і технологіях: формувати вміння застосовувати логічне, алгоритмічне мислення для розв’язування життєвих проблемних ситуацій;

 уміння вчитися впродовж життя: формувати вміння організовувати свою діяльність із використанням програмних засобів для планування та структурування роботи;

 соціальна та громадянська компетентності: формувати вміння дотримуватися правил безпеки життєдіяльності під час роботи з ІТ-пристроями;

Очікувані результати:

У процесі уроку учні зможуть:

повторити основний теоретичний матеріал з теми;
удосконалити свої вміння та навички знаходити площі фігур;
поглибити свої знання історичним матеріалом;
розвивати техніку обчислення, просторову уяву.

Обладнання: комп’ютери, ноутбук, проектор, роздавальний матеріал.

Тип уроку: комбінований.

Форма проведення: практичне заняття.

Хід уроку

І. Організаційний момент

ІІ. Повідомлення теми та завдань уроку

$C:\Users\Світлана\Desktop\Word Art.jpeg$

Завдання

Протягом уроку учні зможуть:

- повторити означення та властивості вивчених многокутників та формули обчислення їх площ;

- закріпити уміння знаходити площі фігур;

- закріпити уміння застосовувати формули для розв'язування прикладних задач;

- поглибити свої знання цікавими фактами з життя;

- удосконалювати вміння оцінювати свої знання, працювати в парах та в групах.

$C:\Users\Світлана\AppData\Local\Microsoft\Windows\INetCache\Content.MSO\CAA679B9.tmp$

Вправа «Очікування».

Учні на переходять за посиланням або QR-кодом і залишають стікер, де одним словом висловлюють свої очікування від уроку.

https://cutt.ly/OxRRD4A

ІІІ. Мотивація навчальної діяльності

Діти, сьогодні ми дізнаємось про те, як геометрія допомагає людям створювати комфортні умови життя.

Дуже давно один давньогрецький мудрець сказав: « Найвищий прояв духу - це розум. Найвищий прояв розуму - це геометрія». Зверніть увагу на слайди і дайте відповідь: «Чи можна без знань геометрії, без знань про многокутники, їх властивостей та формул площ побудувати такі будинки, такі меблі, каміни, так естетично впорядкувати садибу?»

$C:\Users\Світлана\AppData\Local\Microsoft\Windows\INetCache\Content.MSO\DB363D2F.tmp$

ІІІ. Актуалізація опорних знань

Онлайн тестування

https://naurok.com.ua/test/join?gamecode=3184966

IV. Формування вмінь та навичок

Презентація «Історія походження площі многокутника» (група учнів)

Презентація збірника задач «Практичне застосування обчислення площ фігур у повсякденному житті» (група учнів).

Площі деяких многокутників учені Єгипту вміли визначати за кілька тисячоліть до нашої ери. Життя змушувало це робити. Річка Ніл, розливаючись, щоразу змивала межі полів, і землеміри, знов і знов відновлювали їх.
Вимірювати площі земельних ділянок доводиться також геодезистам, маркшейдерам, шляховикам, будівельникам, косарям, лісникам, трактористам, дизайнерам ландшафту; площі оброблювальних поверхонь – штукатурам, мулярам, паркетникам, покрівельникам ,малярам, столярам, а площі витрачених матеріалів – текстильникам , жерстяникам, склярам, бухгалтерам і багатьом іншим фахівцям.

Поняття площі добре зрозуміле на рівні повсякденного досвіду: Ми вимірюємо площу спортивного майданчика або садової ділянки, розраховуємо за площею кількість шпалер або килимового покриття для ремонту кімнати і т.д. Спробуємо надати уявлення про площу певну математичну строгість.
Немає межі творчості людини, якщо вона має та вміє застосовувати знання з геометрії при створені шедеврів.

Частину запропонованих розв’язуємо на уроці, решту використовую як домашнє завдання.

Розв’язування практичних задач, використовуючи можливості Excel, а тим часом 4 учні працюють з 3D-ручкою, створюючи кожен свою фігуру (трапеція, трикутник, прямокутник, ромб) Как работает 3D ручка?

Шаблони фігур для створення 3D-моделей

Практичне завдання 1.
Ділянка під вікнами нашої школи прямокутної форми шириною 3,5м і довжиною у 8 разів більшою. Скільки цибулин тюльпанів треба придбати учням 8-а класу, щоб засадити клумбу, якщо на 0,45м² можна посадити 10 цибулин?

Практичне завдання 2.
Необхідно оштукатурити стіну довжиною 8м і висотою 4,5м, що має три вікна розміром 2м х 1,5м кожне. Знайти площу поверхні стіни, яку необхідно оштукатурити.

Практичне завдання 3.
Сад має форму прямокутника зі сторонами 580м і 350м. Який виторг дав сад після продажу яблук, якщо з 1га зібрано по 35т яблук і кожна тонна продана в середньому по 1100грн?

Обчислення площ фігур, створених 3D-ручкою

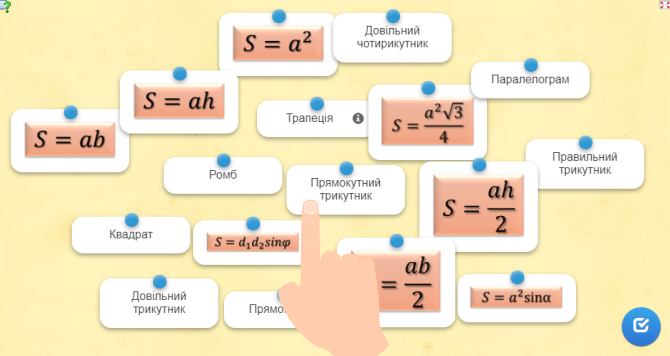
Інтерактивна вправа «Знайди пару»

https://learningapps.org/view5247137

Презентація «Практична орігаметрія» (група учнів).

А що таке орігаметрія?

Орігамі - мистецтво складання фігур з паперу без застосування ножиць.

Геометрія в первісному своєму значенні розумілася як наука про фігурах, про взаємне розташування і розміри їх частин, а також про перетворення фігур.

Геометрична діяльність:

1. навчаємо графічним дій,

2. навичок конструювання,

3. формуємо метричні подання.

Орігаметрія - це поєднання орігамі і геометрії, яка несе в собі оригінальність іншого підходу до геометричних задач.

В орігаметрії вважається:

Роль прямих будуть відігравати краї аркуша і лінії згинів, що утворюються при його згинанні.

Роль точок - вершини кутів листа і точки перетину ліній згинів один з одним або з краями листів.

Термін «технологія» походить від латинського слова construere, що означає - створення моделі, побудова, приведення в певний порядок і взаємовідносини різних окремих предметів, частин, елементів. Вибір саме моделювання з орігамі визначається доступністю для використання на уроці і вдома.

Японське прислів'я говорить:

Розкажи мені - я почую,

Покажи мені - я запам'ятаю,

Дай мені зробити самому -

Я зрозумію!"…

Моя робота розпочалася з вибору фігур, які я буду робити. Спочатку планував зробити лебедя. Купила кольоровий двосторонній папір та папір білого кольору.

$N:\проект оригами\проект оригами 2\5a36ad.jpg$ $H:\проектная деятельность 20мая\оригами\1042[1].jpg$

Якщо довгу і коротку сторону формату А4 розділити на 4 рівні частини і розрізати по намічених лініях, то вийде 16 прямокутників, приблизно 53× 74 мм.

Лебедь из бумаги (оригами)

Якщо довгу сторону формату А4 розділити на 8 частин, а коротку на 4 частини, то вийде 32 прямокутника 37 × 53 мм. Залежно від того на скільки частин ми розділимо лист А4, трикутні модулі матимуть різні розміри. Я вирішила, зробити лебедя з великих модулів. (Великими ми називаємо модулі, якщо лист А4 розділений на 16 прямокутників.) Приступаємо до виготовлення модулів.

$C:\Users\Світлана\AppData\Local\Microsoft\Windows\INetCache\Content.MSO\121001CF.tmp$ Математичні розрахунки

На виготовлення лебедя (біло-зеленого) потрібно:

- 190 білих модулів

- 110 зелених модулів.

Оскільки з одного листа отримується 16 модулів, то мені потрібно 190/16=11(ост.14), тобто 12 аркушів білого паперу, та 110/16=6(ост.14),

тобто 7 аркушів зеленого паперу.

Розмір листа А4	210*297 мм	S =62370 мм²
Розмір одного прямокутника	52,5*74,25 мм	S = 3898,125 мм²
Кількість білих модулів	190 шт	S =740643,75мм²
Кількість зелених модулів	110 шт	S=428793,75мм²
Всього	300 шт	S=1169437,5 мм²

Крім того, я вирахувала приблизну площу поверхні мого лебедя. Я розбила поверхню на фігури, площу яких можна обчислити. Розгортка тулуба являє собою прямокутник, площа якого обчислюється за формулою: S= a ∙ b , де a= 23см, b=7см.

S= 23 ∙ 7=161(см²)

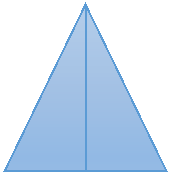Хвіст лебедя та грудка - це трикутники. Формулу площі трикутника я знайшов в довіднику. Також дізналася, що таке висота трикутника і що є основою трикутника.

S= ,

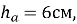a=8см.
S=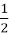6∙8=24(см²)-грудка

2) a=9см.

S=6,5∙9=15,75(см²)-хвіст

3)Дзьоб – прямокутний рівнобедрений трикутник, площу якого обчислюємо за формулою: S= , де .

S=(см²)

Шия являє собою прямокутний паралелепіпед зі сторонами:

а=7см, b= 2см, c= 0,3см.

S= 2ab+2ac+2bc=2(ab+ac+ bc).

S= 2(7×2+7×0,3+2×0,3)=33,4(см²), отже площа поверхні всього лебедя

S= 24+15,75+2+33,4=75,15(см²).

Знайомство з грою «Танграм».

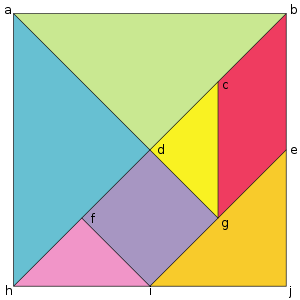Танграм - це стародавня китайська головоломка. У набір головоломки "Танграм" входить квадрат, розрізаний на п'ять трикутників (два великих, один середній і два маленьких), квадрат, рівний за розмірами двох маленьких трикутникам, і паралелограм, по площі рівний квадрату. З цих геометричних фігур головоломки "Танграм" можна скласти кілька сотень силуетів людей, тварин, предметів домашнього вжитку, іграшок, цифр, букв і так далі.

Кожна група учнів отримує конверт, в якому знаходиться комплект різнокольорових геометричних фігур. Завдання: скласти квадрат із цих фігур.
V. Підсумок