Краматорська спеціальна  школа  №18 Донецької обласної ради

               

 

 

 

                                                                                                 Методична розробка з розв’язку

 завдань з математики

 

  

 

 

                                                                                                            Для того, щоб навчитися розв'язувати задачі, треба розібратися

в тому, що вони являють собою, як вони влаштовані, з яких

               складових частин вони складаються, які інструменти, за                допомогою яких виробляється рішення завдань. Одну і ту ж задачу

можна вирішити різними арифметичними способами. Вони

                                                                                                 відрізняються один від одного логікою міркувань, виконуваних у процесі розв’язку задачі.

 

               

               

               

               

  Учитель вищої кваліфікаційної категорії  математики і фізики: 

                                                                   Краматорськ                                                                                               Маханьковська І.В.

 

Математику вже навіть задля того треба вивчати, що вона розум до     ладу приводить.

М. В. Ломоносов

 

Перша умова, якої треба дотримуватися у математиці,— це бути точним, друга — бути ясним і, наскільки можливо, простим. Л. Карно

 

 

 

 

 

 

 

 

 

             

4.          Співставлення задач на спільну роботу, в яких спільна продуктивність являє собою суму продуктивностей кожного виконавця.

5.          Співставлення задач на спільну роботу, в яких спільна продуктивність являє собою різницю продуктивностей виконавців.

 

1 спосіб  розв’язування задач на спільну роботу:

 1) знаходимо загальний виробіток одного виконавця;  2) знаходимо загальний виробіток іншого виконавця;  3) відповідаємо на запитання задачі.

2 спосіб 

1) знаходимо продуктивність спільної праці;  2) відповідаємо на запитання задачі.   

План розв’язування

1)        першою дією знаходимо продуктивність;  

2)        другою дією знаходимо продуктивність виконавця; 

3)        третьою дією знаходимо продуктивність; 4)  четвертою дією відповідаємо на запитання задачі.   

 

 

 

 

 

 

 

 

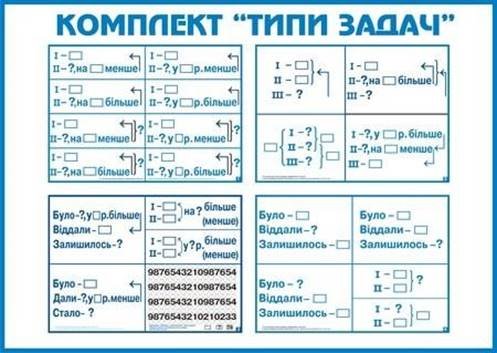
Види задач.

•      За характером вимог задачі:

1)      на знаходження невідомого;

2)      на доведення; 3) на перетворення.

•      По відношенню до теорії:

1)      стандартні; 2) нестандартні.

•      За характером об’єктів: 1) математичні; 2) практичні.

Етапи рішення задачі. Сприйняття і осмислення завдання. 

Прийоми виконання: 

1.  Правильне читання задачі (правильне прочитання слів і речень, правильна розстановка логічних наголосів) у випадку, коли завдання задана текстом.

2.  Правильне слухання при сприйнятті завдання на слух. 

3.  Уявлення ситуації, описаної в задачі (створення зорового, можливо, слухового і кінестетичного образу).  4. Розбиття тексту на смислові частини.

         -    заміна буквених даних числовими; 

5.                  Переформулювання тексту задачі (зміна тексту або побудова словесної моделі):

-          заміна терміна змістовним описом; 

-          заміна змістовного опису терміном;

-          заміна деяких слів синонімами або іншими словами, близькими за змістом; 

-          вилучення частини тексту, яка не впливає на результат рішення; 

-          заміна деяких слів, термінів словами, що позначають більш загальний або більш приватне поняття;

-          зміна порядку слів і (або) речень; 

-          доповнення тексту поясненнями;

-          заміна числових даних іншими, більш наочними;

-          заміна числових даних буквеними; 

-          введення довільних одиниць величин і пов'язані з цим інші зміни тексту. 

6.                  Побудова математичної моделі задачі: - предметної (показ завдання на конкретних предметах).  

Послідовність таких етапів: 

1)  аналіз задачі; 

2)  побудова моделі; 

3)  пошук способу рішення ( складання плану рішення ); 

4)  запис рішення;

5)  перевірка рішення;

6)  дослідження задачі та її рішення;

7)  формулювання відповіді;

8)  навчально-пізнавальний аналіз задачі і її рішення. Методика розв’язування  задач на рух

Під час роботи над задачами на рух можна виділити такі основні поняття, без усвідомлення яких неможливе їх правильне розв'язування. 1. Зустрічний рух:

–  швидкість зближення;

–  час руху до зустрічі (час зближення), якщо два тіла одночасно (неодночасно) почали рухатися назустріч одне одному з однаковими (неоднаковими) швидкостями.

 год – це час, за який можна заповнити

басейн при використанні обох труб разом.

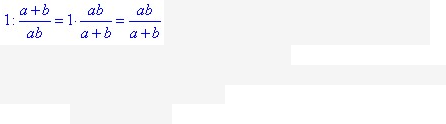Ще раз проаналізуйте чому так, оскільки багато школярів подібні задачі розв'язують неправильно.

Відповідь: a•b/(a+b) – Г.

 

 

Приклад 2. Басейн наповнюється через першу трубу за 4 години,
а через другу – за 6 годин. Яку частину басейну залишиться
наповнити після спільної роботи обох труб протягом 2 годин?

2.Задача на спільну роботу (не дано продуктивність кожного виконавця), в яких спільна продуктивність являє собою суму продуктивностей кожного виконавця.

 

 

3. Задача на спільну роботу (не дано продуктивність кожного виконавця), в яких спільна продуктивність являє собою різницю продуктивностей виконавців.

3)  20 · 50 = 1000 (гривень) — татові; 

4)  30 · 20 = 600 (гривень) — мамі;

5)  10 · 20 = 200 (гривень) — синові.

Відповідь. 1000 грн — татові; 600 грн — мамі, 200 грн — сину.

ІІ спосіб

 

Нехай х — це вартість обробки одного рядка (одна частина — коефіцієнт пропорційності), тоді тато заробив 50х (грн), мама — 30х(грн), син — 10х (грн). А за умовою задачі разом вони заробили 1 800 грн. Маємо рівняння:

 

50х + 30х + 10х = 1800; 90х = 1800; х = 1800 : 90; х =20. Отже, татова частина 50 · 20 = 1 000 грн; мамина — 30 · 20 = 600 грн, синова — 10 · 20. = 200 грн. 

 

Типи  задач на спільну роботу

Приклад 1. Басейн заповнюють водою через першу трубу за a години,
а через другу – за b годин.
Через скільки годин можна заповнити басейн при використанні обох
труб разом?

1.Задача на спільну роботу, в яких дано продуктивність кожного виконавця.

Задача 1. З пристані Київ до пристані Кременчук вийшов теплохід, і одночасно йому назустріч з пристані Кременчук вийшов катер. Теплохід ішов зі швидкістю 30 км/год, а катер – 24 км/год. Через 5 год вони зустрілися. Яка відстань між пристанями? Під час повторення змісту задачі вчитель креслить на дошці ілюстрацію:

 

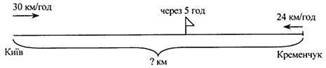
Бесіда. Що означає: «Через 5 год вони зустрілися»? (Теплохід і катер з моменту виходу до моменту зустрічі були в дорозі 5 год.) Яку відстань пройшов за 5 год теплохід? («Від пристані Київ до прапорця», – показує один учень біля дошки.) Яку відстань пройшов катер за 5 год? (Другий учень показує на кресленні.) То з яких двох частин складається шукана відстань між пристанями? (З відстаней, які пройшов кожен теплохід за 5 год.) Чи можемо ми взнати відстань, яку пройшов теплохід до зустрічі? (Можемо, бо відомо його швидкість і час руху до зустрічі.) Чи можемо взнати відстань, яку пройшов до зустрічі катер? (Можемо.)

А коли обидві відстані будуть відомі, про що зможемо дізнатися? (Про відстань між пристанями.) Давайте запишемо розв'язання виразом. Що знайдемо в першій дії? Якою дією? (Вчитель пише на дошці, а учні в зошитах: 30 • 5.) Про що дізнаємося в другій дії? Якою дією? Поруч з'являється другий запис: 30 • 5; 24 • 5. Про що дізнаємося в третій дії? Чого бракує, щоб скласти остаточний вираз? (Вписують знак «+»: 30 • 5 + 24 • 5.) Чи потрібні дужки? Учні усно обчислюють проміжні результати. Записи мають вигляд: 30 • 5 + 24 • 5 = 150 + 120 = 270 (км).

2. Рух у протилежних напрямках:

–  швидкість віддалення;

–  час віддалення, якщо два тіла почали одночасно (неодночасно) рухатися з одного пункту у протилежних напрямках з однаковими (різними) швидкостями.

3. Рух в одному напрямі: – швидкість зближення (віддалення); – час зближення (віддалення).

Задача 2. Два літаки одночасно вилетіли з аеродрому в протилежних напрямках. Через півгодини після вильоту відстань між ними була 720 км. Перший літак летів зі швидкістю 15 км/хв. З якою швидкістю летів другий літак? Графічна схема до цієї задачі:

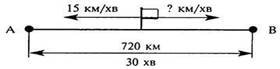 Запитання до учнів під час аналізу задачі:

–  Що відомо про рух першого літака і про що можна дізнатися?

–  Яка відстань між літаками була через півгодини після вильоту?

–  Чи можна знайти відстань, яку пролетів другий літак?

–  Про що запитується в задачі?

–  Які дії треб виконати, щоб відповісти на запитання задачі?

Розв'язання:

1) 15 • 30 = 450 (км) – пролетів перший літак; 2) 720 – 450 = 270 (км) – пролетів другий літак; 3) 270: 30=9 (км/хв) – швидкість другого літака.

Відповідь. 9 км/хв.

 

3. Рух за течією чи проти течії:

–  власна швидкість катера (моторного човна, тощо);

–  швидкість катера за течією;

–  швидкість катера проти течії;

–  швидкість зближення і час зближення, коли катер наздоганяє пліт; – швидкість зближення і час зближення, коли катер рухається назустріч плоту;

–  швидкість віддалення і час віддалення, коли катер і пліт рухаються з одного пункту у протилежних напрямках.

 

4. Середня швидкість руху:

–  середня арифметична величина;

–  середня швидкість як середня арифметична величина Запитання до учнів під час аналізу задачі:

–  Що відомо про рух першого літака і про що можна дізнатися?

–  Яка відстань між літаками була через півгодини після вильоту?

–  Чи можна знайти відстань, яку пролетів другий літак?

–  Про що запитується в задачі?

–  Які дії треб виконати, щоб відповісти на запитання задачі?

 

Методика ознайомлення учнів із прикладами залежностей між величинами

У початкових класах учні ознайомлюються з вимірюванням деяких величин (довжина, площа, маса, час), встановлюють зв‘язки між величинами під час розв’язування текстових задач: ціна, кількість і вартість; маса одного предмета, кількість предметів і загальна маса; швидкість, шлях і час при рівномірному русі тіла тощо. Якщо названі величини брати попарно, то побачимо різні види залежностей:            прямо пропорційну залежність (вартість і ціна, добуток і множник);       

•  обернено пропорційну залежність  (кількість  і  ціна, дільник  і  частка);

•  лінійну залежність (сума і доданок, маса товару з тарою і

маса самого товару);  

•  квадратичну залежність  (площа  квадрата  і  довжина  його  сторони). Приклад. Сім'я Петренків на літо взяла обробити поле цукрових буряків. Тато Петренко обробив 50 рядків, мама Петренко обробила 30 рядків, а синок Петрик Петренко обробив 10 рядків. За літо сім'я Петренків за обробку поля заробила 1 800 гривень. Як ці гроші треба поділити між татом, мамою та їх сином?

Після обговорення задачі доходимо висновку: в задачі треба поділити число 1 800 на 3 нерівних частини, що відповідають (пропорційні) числам 50, 30 і 10.

І спосіб  

Тому:1) 50 + 30 + 10 = 90 (рядків) обробили;

2)  1800 : 90 = 20 (гривень) — за 1 рядок;

3)  20 · 50 = 1000 (гривень) — татові; 

4)  30 · 20 = 600 (гривень) — мамі;

5)  10 · 20 = 200 (гривень) — синові.

Відповідь. 1000 грн — татові; 600 грн — мамі, 200 грн — сину.

ІІ спосіб

 

Нехай х — це вартість обробки одного рядка (одна частина — коефіцієнт пропорційності), тоді тато заробив 50х (грн), мама — 30х(грн), син — 10х (грн). А за умовою задачі разом вони заробили 1 800 грн. Маємо рівняння:

 

50х + 30х + 10х = 1800; 90х = 1800; х = 1800 : 90; х =20. Отже, татова частина 50 · 20 = 1 000 грн; мамина — 30 · 20 = 600 грн, синова — 10 · 20. = 200 грн. 

 

Типи  задач на спільну роботу

1.Задача на спільну роботу, в яких дано продуктивність кожного виконавця.

Приклад 1. Басейн заповнюють водою через першу трубу за a години, а через другу – за b годин. 

Через скільки годин можна заповнити басейн при використанні обох труб разом? 

 

Обчислення:Нехай 1/a - частина басейну, яку заповнить І труба за

1год; 

1/b - частина басейну, яку заповнить ІІ труба за 1год; 

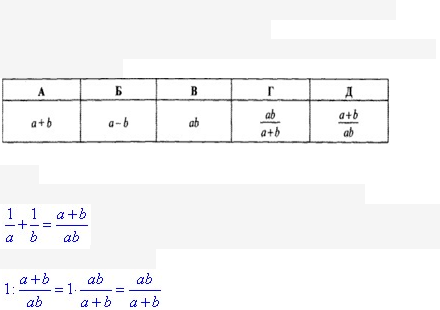 - частина басейну, яку наповнять обидві труби за 1 год, працюючи разом. 

 год – це час, за який можна заповнити

басейн при використанні обох труб разом.

Ще раз проаналізуйте чому так, оскільки багато школярів подібні задачі розв'язують неправильно.

Відповідь: a•b/(a+b) – Г.

 

 

2.Задача на спільну роботу (не дано продуктивність кожного виконавця), в яких спільна продуктивність являє собою суму продуктивностей кожного виконавця.

Приклад 2. Басейн наповнюється через першу трубу за 4 години,
а через другу – за 6 годин. Яку частину басейну залишиться
наповнити після спільної роботи обох труб протягом 2 годин?

 

 

3.          Задача на спільну роботу (не дано продуктивність кожного виконавця), в яких спільна продуктивність являє собою різницю продуктивностей виконавців.

4.          Співставлення задач на спільну роботу, в яких спільна продуктивність являє собою суму продуктивностей кожного виконавця.

5.          Співставлення задач на спільну роботу, в яких спільна продуктивність являє собою різницю продуктивностей виконавців.

 

1 спосіб  розв’язування задач на спільну роботу:

 1) знаходимо загальний виробіток одного виконавця;  2) знаходимо загальний виробіток іншого виконавця;  3) відповідаємо на запитання задачі.

2 спосіб 

1) знаходимо продуктивність спільної праці;  2) відповідаємо на запитання задачі.   

План розв’язування

5)        першою дією знаходимо продуктивність;  

6)        другою дією знаходимо продуктивність виконавця; 

7)        третьою дією знаходимо продуктивність; 8)  четвертою дією відповідаємо на запитання задачі.