Конспект дистанційного уроку: «Розв’язування задач по темі «Суміжні та вертикальні кути»».

Тема дистанційного уроку: «Розв’язування задач

по темі «Суміжні та вертикальні  кути»».

Мета: домогтися розуміння учнями змісту наслідків з теорем про суміжні та вертикальні  кути та змісту понять “наслідок”, “посилання”; використовуючи знання теорем про суміжні та вертикальні кути та їх наслідки, виробити вміння розв’язувати задачі на обчислення , в яких йдеться про суміжні иа вертикальні кути.

Тип уроку: застосування знань, умінь та навичок.

Хід уроку

Розгляньте розв’язання задач і за зразком та  виконайте домашне завдання

Задача 1 Знайдіть суміжні кути, якщо один з них на 28° більший від суміжного з ним кута.

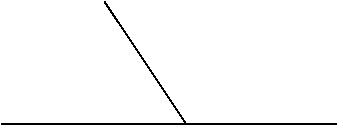                                                                             Дано: ˂1 і ˂2 – суміжні

˂1 на 28° більший від ˂2

  2                1                                          Знайти: ˂1 і ˂2

Розв’язання

1. Нехай ˂1 і ˂2 – суміжні кути данні за умовою, ˂1 на 28° більший від ˂2.

2. Нехай ˂2 – х (°), тоді ˂1 – х + 28°. х + х + 28° - сума градусних мір кутів, а за Теоремою про суміжні кути = 180°. Складаємо рівняння

х + х + 28° = 180°

х + х = 180° - 28°

2х = 152°

х = 152° : 2

 х = 76° -  ˂2

3. ˂1 = 180° - 76° = 104° - за Теоремою про суміжні кути.

Відповідь : 104°;  76°.

Задача 2 Знайдіть суміжні кути, якщо вони відносяться як 7:2

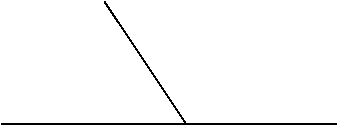                                                                             Дано: ˂1 і ˂2 – суміжні

                                                                    ˂1 : ˂2  =  19 : 17

  2                1                                          Знайти: ˂1 і ˂2

Розв’язання

1. Нехай ˂1 і ˂2 – суміжні кути данні за умовою, ˂1 : ˂2  =  19 : 17.

2. Нехай– х (°) – коефіцієнт пропорційності, тоді ˂1 – 19х , а ˂2 – 17х.

19х + 17х - сума градусних мір кутів, а за Теоремою про суміжні кути = 180°. Складаємо рівняння

19х + 17х = 180°

36х  = 180°

х = 180° : 36

 х = 5° -  коефіцієнт пропорційності.

3. ˂1 = 19х = 19*5  = 95°.

4. ˂2 = 17х = 17*5 = 85°.

Відповідь : 95°;  85°.

Задача 3 Знайдіть кути, утворенні при перетині двох прямих, якщо різниця двох із них дорівнює 54°.

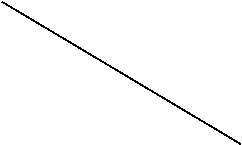                             3            а                                                  Дано: а х в

                                                                        ˂1  - ˂3 = 54°

                       2                1                                             Знайти: ˂1, ˂2, ˂3, ˂4

                                       4              в

Розв’язання

1. Нехай а х в, утворилися  ˂1 , ˂2, ˂3, ˂4. 

У них : ˂1 = ˂2

             ˂3 = ˂4                                                     

              ˂1 + ˂3 = 180° - як суміжні.   

2. Нехай ˂3 – х (°), тоді ˂1 – 54° + х . х + 54° + х - сума градусних мір кутів, а за Теоремою про суміжні кути = 180°. Складаємо рівняння

х + 54° + х = 180°

х + х = 180° - 54°

2х = 126°

х = 126° : 2

 х = 63° -  ˂3

3. ˂1 = 180° - 63° = 117° - за Теоремою про суміжні кути

4. ˂1 = ˂2 = 117°

5. ˂3 = ˂4 = 63°

Відповідь : 117°;  117°;  63°; 63°.

Домашне завдання

1. Знайти величину кожного з кутів, що утворилися при перетині двох прямих, якщо сума двох із них дорівнює 52°.

2. Знайдіть суміжні кути, якщо один з них на 48° менший від суміжного з ним кута.

3. Знайдіть суміжні кути, якщо вони відносяться як 21:24