Конспект по темі Многогранники 11 клас
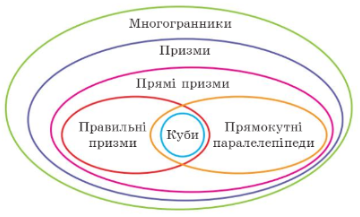
Призма

|
Пряма призма |
Правильна призма |
Похила призма |
|
Призму називають прямою, якщо її бічні ребра перпендикулярні до основи |
Призму називають правильною, якщо вона є прямою, а її основа – правильний многокутник наприклад: правильний трикутник, квадрат |
Якщо призма не є прямою – то вона похила |
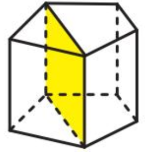 Діагональний переріз призми
Діагональний переріз призми
Переріз призми площиною, яка проходить через два бічних ребра, що не належать одній грані, перетинає основи призми по діагоналях називають діагональним перерізом
Формула площі призми
Площа повної поверхні: Sп=Sб+2Sосн
Sб – площа бічної поверхні призми (формула нижче), Sосн – площа основи (шукається в залежності від того, який многокутник в основі)
Площа бічної поверхні: Sб=Росн*b
Sб=Росн*H
Sб – площа бічної поверхні призми, Росн – периметр основи (сума всіх сторін), b – довжина бічного ребра, Н – висота призми
Об’єм призми: V=Sосн*h
Висотою призми називають перпендикуляр, опущений з якої-небудь точки площини однієї основи на площину другої основи.
Кожне бічне ребро прямої призми є її висотою, а усі бічні грані прямої призми – прямокутники
Паралелепіпед
Паралелепіпед – це призма, основи якої є паралелограми.
|
Прямий паралелепіпед |
Прямокутний паралелепіпед |
|
Прямим називають той паралелепіпед, у якого бічні ребра перпендикулярні до площини основи |
Прямокутним називають прямий паралелепіпед, у якого в основі прямокутник |
Одним із різновидів паралелепіпеда є куб.
Куб – прямокутний паралелепіпед, у якого всі виміри рівні, а усі грані є квадратами (висота=довжина основи=ширина основи)
Діагоналі паралелепіпеда перетинаються, та точкою перетину діляться навпіл.

 Квадрат будь-якої діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів його вимірів.
Квадрат будь-якої діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів його вимірів.
АС12 =АВ2+AD2+AA12
Звідси випливає, що діагоналі прямокутного паралелепіпеда рівні
Формули площі ті ж самі, що й в призмі:
Площа повної поверхні: Sп=Sб+2Sосн
Площа бічної поверхні: Sб=Росн*b
Sб=Росн*H
Об’єм паралелепіпеда: V=Sосн*h
Об’єм куба: V=a3
Піраміда

Висота піраміди – перпендикуляр, опущений з вершини піраміди на площину основи (у трикутника – це точка перетину медіан, у чотирикутника – точка перетину діагоналей)

Переріз піраміди площиною, яка проходить через два бічних ребра, що не належать одній грані та перетинає площину основи піраміди по діагоналі називають діагональним перерізом піраміди
Піраміда є правильною, якщо її основа правильний многокутник (правильний трикутник, квадрат), а основа висоти піраміди є центром цього многокутника
Одним із різновидів піраміди є правильний тетраедр.
Тетраедр – правильна трикутна піраміда всі грані якої правильні трикутники.
Апофема

Апофемою правильної піраміди називають висоту бічної грані, що проведена з вершини піраміди до середини сторони основи.
Формула площі піраміди
Площа повної поверхні: Sп=Sб+Sосн
Sб – площа бічної поверхні призми (формула нижче), Sосн – площа основи (шукається в залежності від того, який многокутник в основі)
Площа бічної поверхні: Sб=![]() Росн*m
Росн*m
Sб – площа бічної поверхні призми, Росн – периметр основи (сума всіх сторін), m – довжина апофеми правильної піраміди.
Об’єм піраміди: V=![]() Sосн*H
Sосн*H
Формулювання в задачах
|
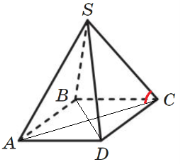
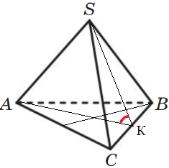
Бічне ребро нахилене до основи під кутом _ градусів
Мова йде про кут між ребром і діагоналлю чотирикутника, або якщо в основі трикутник, то це градусна міра між ребром і медіаною опущеною з кута вершини трикутника |
|
|
Бічне ребро утворює з площиною основи кут_градусів
Мова йде про лінійний кут двогранного кута, якщо простіше, то це кут між апофемою та основою |
|
Зрізана піраміда

Висотою зрізаної піраміди називають перпендикуляр, опущений з будь-якої точки площини однієї основи на площину другої основи.
Апофемою правильною зрізаної піраміди називають відрізок, який сполучає середини ребер основ, що належать одній бічній грані.
Формула площі піраміди
Площа бічної поверхні: Sб=![]() (Росн+росн)*m
(Росн+росн)*m
Росн, росн – периметри двох основ


про публікацію авторської розробки
Додати розробку