Конспект по темі звичайні дроби та дії з ними
Дроби
|
Звичайний дріб |
|
|
|
- неправильний дріб
|
|
коли чисельник більше за знаменник |
|
- мішаний дріб |
5 |
коли є ціла і дробова частина |
|
Десятковий дріб |
0,35 |
дріб, який пишеться через кому: зліва від коми – цілі, справа – дробові значення |
Щоб перейти до пункту натисни одночасно Ctrl+пункт, який потрібно відкрити
1. Як перевести звичайний дріб у десятковий і навпаки:
2. Як мішаний дріб записати у вигляді неправильного дробу і навпаки:
4. Додавання та віднімання звичайних дробів
7. Порівняння звичайних дробів
1. Як перевести звичайний дріб у десятковий і навпаки:
-
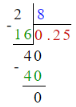 треба чисельник поділити на знаменник, наприклад:
треба чисельник поділити на знаменник, наприклад:
![]() = 2:8 = 0,25
= 2:8 = 0,25
- якщо є ціла частина:
![]() = 2:8 = 0,25, але у нас є 2 цілі, тому відповідь 2,25
= 2:8 = 0,25, але у нас є 2 цілі, тому відповідь 2,25
- щоб перевести десятковий дріб в звичайний треба:
0,35 – в чисельник пишемо те число, яке після коми, а в знаменник пишемо одиничку з такою кількістю нулів, скільки знаків після коми, отже: ![]()
0,134 – ![]() 0,54 -
0,54 - ![]() 0,003 -
0,003 - ![]()
- якщо є ціла частина, то записуємо у вигляді мішаного дробу:
5,012 – ![]() 1,09 -
1,09 - ![]() 15,8 -
15,8 - ![]()
2. Як мішаний дріб записати у вигляді неправильного дробу і навпаки:
Наприклад ми маємо ![]() , щоб перевести мішаний дріб у неправильний нам треба:
, щоб перевести мішаний дріб у неправильний нам треба:
- ціле число*знаменник+чисельник
- те що вийшло пишемо в чисельник, я знаменник залишається незмінним
![]() = 7*9+2 =
= 7*9+2 = ![]()
![]() = 4*5+1 =
= 4*5+1 = ![]()
![]() = 11*6+5 =
= 11*6+5 = ![]()
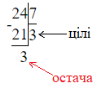 Якщо ми маємо неправильний дріб (коли чисельник більше за знаменник), нам треба виділити цілу частину (записати у вигляді мішаного дробу). Для цього ми чисельник ділимо на знаменник, цілі записуємо, остача залишається в чисельнику, а знаменник не змінний, наприклад:
Якщо ми маємо неправильний дріб (коли чисельник більше за знаменник), нам треба виділити цілу частину (записати у вигляді мішаного дробу). Для цього ми чисельник ділимо на знаменник, цілі записуємо, остача залишається в чисельнику, а знаменник не змінний, наприклад:
![]() = 24:7 = 3 цілі (3 остача) = 3
= 24:7 = 3 цілі (3 остача) = 3![]()

![]() = 15:9 = 1 ціла (6 остача) = 1
= 15:9 = 1 ціла (6 остача) = 1![]()
Остача – це число, яке вже не можна поділити на дільник, в наших випадках остачу 3 вже не можна поділити на 7, а в другому випадку 6 уже не можна поділити на 9.
3. Скорочення дробів:
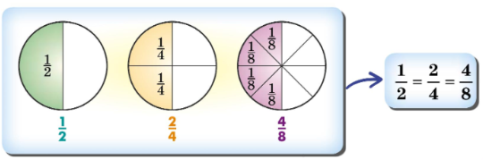
Ми бачимо що у всіх трьох прикладах ми отримуємо половину, томі ці три дроба рівні між собою, а довести це ми можемо скоротивши дріб ![]() та дріб
та дріб ![]()
![]() - і чисельник і знаменник ми можемо націло поділити на 2, тоді 2:2=1, а 4:2=2
- і чисельник і знаменник ми можемо націло поділити на 2, тоді 2:2=1, а 4:2=2
отже ![]()
![]() - і чисельник і знаменник ми можемо націло поділити на 4, тоді 4:4=1, а 8:4=2
- і чисельник і знаменник ми можемо націло поділити на 4, тоді 4:4=1, а 8:4=2
отже ![]()
Дріб називається нескоротним, коли ми вже не можемо чисельник і знаменник поділити на однакове число (крім 1).

А з цього випливає основна властивість дробу, що якщо ми чисельник і знаменник дробу помножимо на однакове число, то значення дробу не зміниться (окрім 0)!

4. Додавання та віднімання звичайних дробів
Ми можемо додавати та віднімати тільки ті дроби, які мають однаковий знаменника:
![]() +
+ ![]() – у знаменнику першого і другого дроба стоїть 7, тому ми додаємо чисельники, а знаменник записуємо спільний =
– у знаменнику першого і другого дроба стоїть 7, тому ми додаємо чисельники, а знаменник записуємо спільний = ![]() =
= ![]()
Якщо дроби мають різні знаменники, тоді нам треба знайти СПІЛЬНИЙ ЗНАМЕННИК!
Спільний знаменник – число, яке ми зможемо націло поділити і на перший і на другий знаменник.
![]() – знаменники різні, а отже нам треба знайти таке число, яке поділиться на 3 і на 14, для цього є певні лайфхаки:
– знаменники різні, а отже нам треба знайти таке число, яке поділиться на 3 і на 14, для цього є певні лайфхаки:
|
в нашому випадку більше число 14, спробуємо 14:3, націло не ділиться, переходимо до 2 пункту. 14*2=28, 28 на 3 не ділиться, ідемо далі, 14*3=42, 42 на 3 ділиться, значить 42 буде спільним знаменником |
Як знайти спільний знаменник? |
|
1. Спробуй поділити більше число на менше, якщо вийшло, то більше число буде спільним знаменником |
|
|
2. Візьми більше число і поступово множ його на 2, 3, 4 і тд, а результат діли на другий знаменник |
|
|
3. Для будь-яких чисел спільним знаменником буде їх добуток, тому завжди можна перемножити два знаменника і це буде спільним знаменником для обох, АЛЕ: ТОДІ ДРІБ МАЙЖЕ ЗАВЖДИ БУДЕ СКОРОТНИМ, тому його в кінці треба буде скорочувати |
Тепер, коли спільний знаменник знайдено, нам треба записати додаткові множники:
Додатковий множник – це число, яке нам треба домножити до чисельника.

 Щоб знайти додатковий множник: треба новий знаменник поділити на старий знаменник
Щоб знайти додатковий множник: треба новий знаменник поділити на старий знаменник
А тепер додатковий множник ми маємо домножити на чисельники:
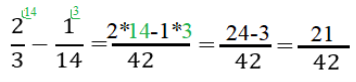
![]() – перевіряємо, чи можемо ми поділити чисельник і знаменник на однакове число: 21 і 42 ділиться на 21, тому скорочуємо чисельник і знаменник на 21 =
– перевіряємо, чи можемо ми поділити чисельник і знаменник на однакове число: 21 і 42 ділиться на 21, тому скорочуємо чисельник і знаменник на 21 = ![]()
Іноді буває, що відразу не видно, що чисельник і знаменник діляться на однакове число, тому це можна перевірити знаючи подільність натуральних чисел:
Подільність натуральних чисел |
|
Якщо у нас додаються/віднімаються мішані дроби (з цілими), то ми окремо додаємо/віднімаємо цілі частини, а окремо дроби (якщо необхідно зводячи їх до спільного знаменника:
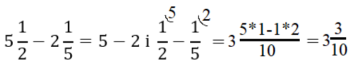
Якщо у нас віднімаються мішані дроби, то ми після зведення до одного знаменника маємо спочатку звернути увагу: чи можемо ми від першого дробу відняти другий дріб?
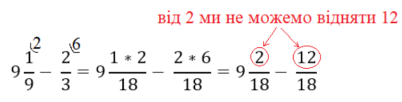
в такому випадку нам треба забрати 1 цілу частину і записати це + у чисельник, додавати треба число яке стало спільним знаменником:
було ![]() від 9 забираємо 1 і записуємо її у чисельник, як +18 (спільний знаменник) = 8
від 9 забираємо 1 і записуємо її у чисельник, як +18 (спільний знаменник) = 8![]() = 8
= 8![]() , тепер ми вже можемо віднімати:
, тепер ми вже можемо віднімати:
![]()
чисельник і знаменник можемо скоротити на 2 і виходить:
![]()

5. Множення звичайних дробів
З множенням, все набагато легше. Бачиш множення двох дробів – чисельник*чисельник, а знаменник*знаменник:
![]()
Але, іноді множення буває складнішим, а відповідь виходить у вигляді скоротного дробу:
![]()
Дріб довелося скорочувати 2 рази, тому що відразу не видно на скільки треба скоротити, через це скорочення може зайняти ще більше часу ніж саме множення. Для цього під час множення треба максимально скоротити  чисельник знаменник:
чисельник знаменник:

Тобто ми максимально скорочуємо чисельник зі знаменником під час множення, щоб легше множити і не скорочувати дріб вкінці.
ЗАБОРОНЕНО СКОРОЧУВАТИ ЧИСЕЛЬНИК З ЧИСЕЛЬНИКОМ
ЗАБОРОНЕНО СКОРОЧУВАТИ ЗНАМЕННИК ЗІ ЗНАМЕННИКОМ
6. Ділення звичайних дробів
Щоб поділити звичайні дроби нам треба дію ділення замінити на дію множення, а другий дріб перевернути:

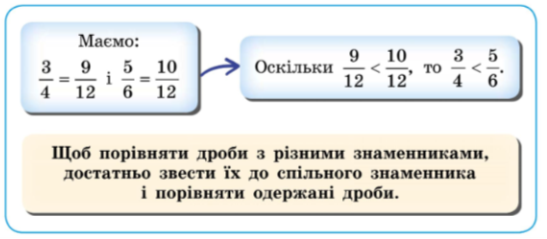
7. Порівняння звичайних дробів



про публікацію авторської розробки
Додати розробку
