Конспект та презентація уроку на тему: "Розв'язування ірраціональних рівнянь" з алгебри та початків аналізу для 10 класу профільного рівня.
Тема: ”Розв'язування
![]() домашньо:
домашньо: ![]() роботи
роботи
|
|
|

Знання можуть бути лише у того, хто мае питання.
Ханс-Георг ГаДамер(1900-2002)
Cnpa6DkHi знання ми отри.иу€мо, коли шука€мо ТДпоТДь на запитання, а не коли ![]() саму вћ)поТДь.
саму вћ)поТДь.
Млойд АлексанДер(1924-2007)
Розминка 1) 1рращональним називаеться...
2) Розв 'язати означае...
З) Основними методами розв ' язування ![]() е.. .
е.. .
4)
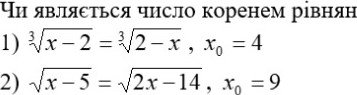 |
При
5) При ![]() обох частин
обох частин ![]() до парного степеня завжди отримуемо . . .
до парного степеня завжди отримуемо . . .
6) kopiHb ![]() який одержують в
який одержують в ![]() перетворень називають...
перетворень називають...
Розминка
Усно
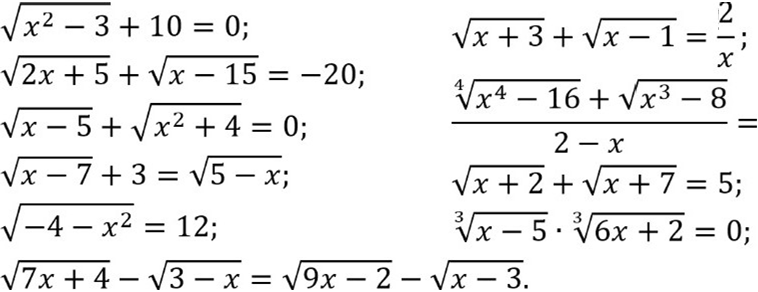
BcTaH0BiTb ![]() та методом його розв ' язування.
та методом його розв ' язування.
 А. шднесення до слепеня; D. ОДЗ; В. замша змжноТ; Е.
А. шднесення до слепеня; D. ОДЗ; В. замша змжноТ; Е.
С. розкладання на

BapiaHT 1 BapiaHT 2
|
|
|
|
с |
D |
Е |
|
|
|
|
с |
D |
Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

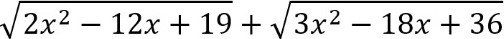 = -2x2 + 12x- 14
= -2x2 + 12x- 14
60![]() = 40 χ- 31
= 40 χ- 31
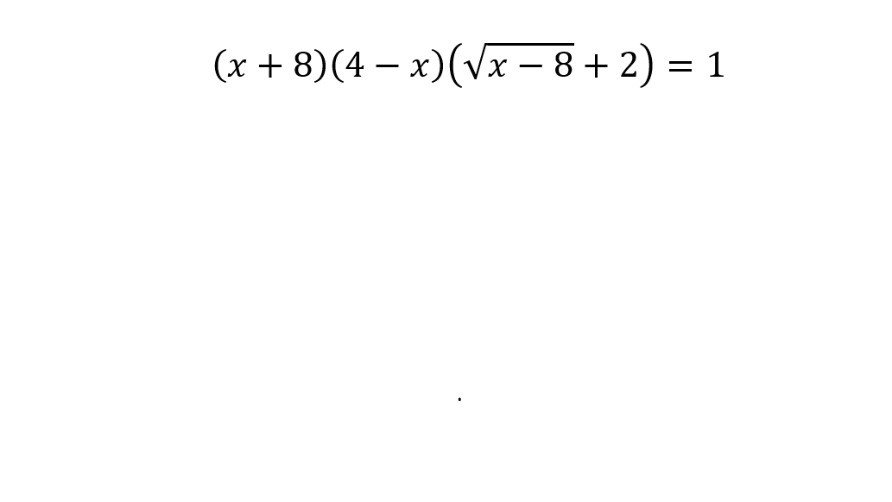
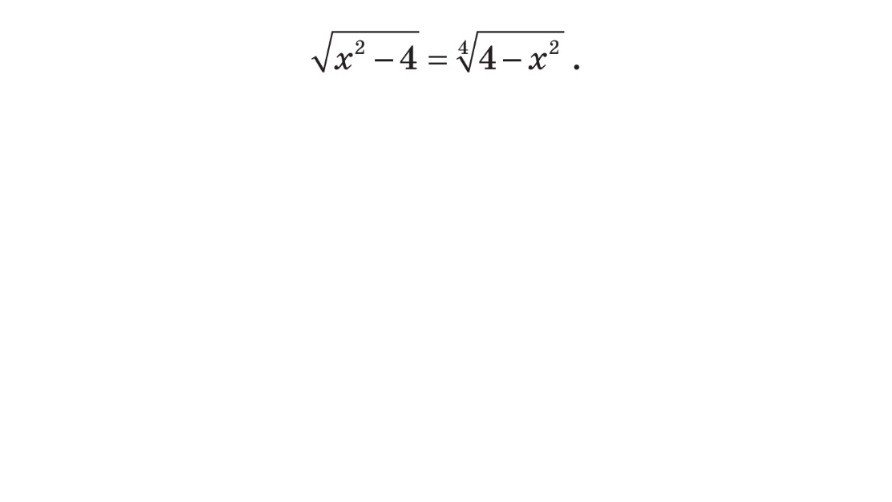

BapiaHT 1
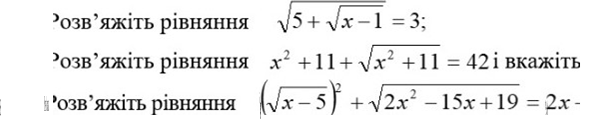 N91.
N91.
N92. найменший k0PiHb
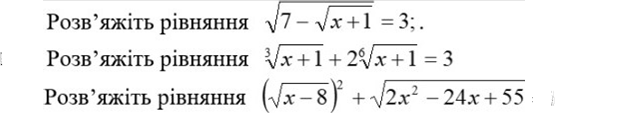 BapiaHT 2 N91.
BapiaHT 2 N91.
МЗ.
![]()
|
|
|
М2 |
|
|
BapiaHT 1 |
17 |
-5 |
6 |
|
BapiaHT 2 |
|
|
9 |

Конспект уроку з алгебри та початків аналізу
для 10 класу профільного рівня.
Підготувала вчителька математики
спеціалізованої школи I-III ступенів № 250
з поглибленим вивченням математики
Деснянського району міста Києва
Масловська Світлана Степанівна
Тема: Розв’язування ірраціональних рівнянь
Мета: Узагальнити і систематизувати знання учнів з теми «Ірраціональні рівняння»; розширити знання новими нестандартними методами розв’язування ірраціональних рівнянь; розвивати навички самоконтролю і самооцінки, взаємопідтримки і взаємодопомоги; виховувати етику та культуру спілкування.
Формувати компетентності:
- загальнокультурну (застосовувати методи самовиховання, орієнтовані на загальнолюдські цінності);
- здоров’язбережувальну (здатність учня дбайливо ставитися до власного здоров’я та здоров’я інших людей);
- інформаційно-комунікаційну (здатність учня використовувати інформаційно-комунікаційні технології та відповідні засоби для виконання завдань);
- предметну(галузеву) (сукупність знань, умінь необхідних для виконання учнями певних дій з метою розв’язання навчальних проблем, задач, ситуацій)
Тип уроку: урок узагальнення і систематизації знань, умінь і навичок.
Обладнання: мультимедійна дошка, роздатковий матеріал, лист оцінки діяльності учня.
Хід уроку:
І. Організаційний етап. Повідомлення теми і мети уроку
Учні записують у зошит дату й тему уроку. (заздалегідь написано на дошці)
Учитель повідомляє мету уроку. Ми повинні:
- узагальнити вивчені методи розв’язування ірраціональних рівнянь;
- ознайомитись з новими нестандартними методами розв’язування ірраціональних рівнянь;
- дати оцінку власної роботи на уроці.
ІІ. Перевірка домашнього завдання
У кожного з вас на столі аркуш для перевірки результатів виконання домашньої самостійної роботи. Прошу виконати перевірку за допомогою таблиці з відповідями та розшифрувати закодоване слово. Бажаю всім успіху!
Варіант 1
Розв'язати рівняння:
Варіант 2
Розв’язати рівняння:
|
Відповідь |
-1 |
0; 3; 4 |
61 |
-2 |
3 |
|
5 |
-1;0 |
1; 3 |
0; 0,4 |
|
Ключ |
Т |
А |
Н |
Н |
Н |
З |
П |
И |
Н |
А |
Варіант І
|
№1 |
№2 |
№3 |
№4 |
№5 |
6 |
|
|
1; 3 |
0; 3; 4 |
3 |
61 |
Я |
|
|
|
|
|
|
Я |
1 варіант закодоване слово – ЗНАННЯ
Варіант ІІ
|
№1 |
№2 |
№3 |
№4 |
№5 |
6 |
7 |
|
5 |
-1;0 |
-1 |
0; 0,4 |
-2 |
Н |
Я |
|
|
|
|
|
|
Н |
Я |
2 варіант закодоване слово – ПИТАННЯ
Епіграфом нашого уроку сьогодні будуть висловлювання:
Знання можуть бути лише у того, хто має питання.
Ханс-Георг Гадамер(1900-2002)
Справжні знання ми отримуємо, коли шукаємо відповідь на запитання, а не коли дізнаємось саму відповідь.
Ллойд Александер(1924-2007)
III. Актуалізація опорних знань
Розминка
Завдання 1.
1) Ірраціональним рівнянням називається…..(рівняння, що містить змінну під знаком кореня або змінна із дробовим показником. ).
2) Розв’язати рівняння означає …….(знайти усі його корені або довести, що їх немає).
3) Основними методами розв’язування ірраціональних рівнянь є
……(через ОДЗ, піднесення обох частин рівняння до одного і того
самого степеня; заміна змінної; графічний і т д .)
4) При піднесені обох частин рівняння до непарного степеня завжди
отримуємо ……(рівняння, рівносильне даному).
5) При піднесені обох частин рівняння до парного степеня завжди
отримуємо ……(рівняння – наслідок).
6) Як називається корінь рівняння, який одержують в результаті нерівносильних перетворень? (сторонній).
Завдання 2.
Чи є число коренем рівняння:
1) ![]() ,
, ![]() 2)
2) ![]() ,
, ![]()
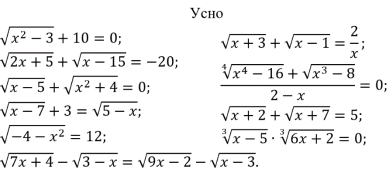 Завдання 3.
Завдання 3.
Знайдіть корені рівняння:
IV. Узагальнення та систематизація знань
Фронтальна робота
Повторення вивчених методів розв’язування ірраціональних рівнянь.
Завдання 4. Встановити відповідність між рівнянням та методом його розв’язування.
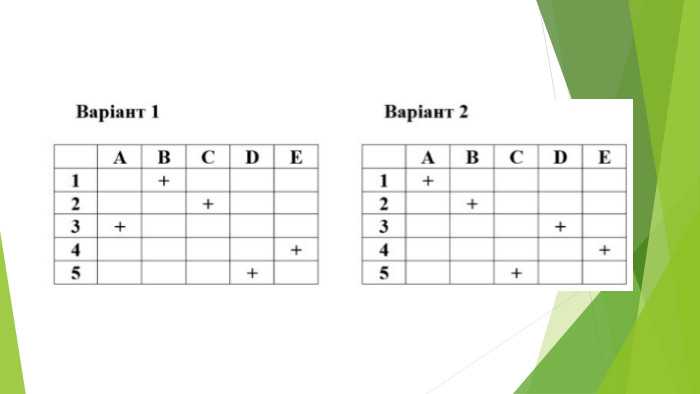
Варіант І
Встановіть відповідність між ірраціональним рівнянням та методом його розв’язування.
- піднесення до степеня;
- заміна змінної;
- розкладання на множники;
- оцінка ОДЗ;
- графічний.
|
Рівняння |
Методи розв’язування |
||||
|
A |
B |
C |
D |
E |
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
3) |
|
|
|
|
|
|
4) |
|
|
|
|
|
|
5) |
|
|
|
|
|
Варіант ІІ
Встановіть відповідність між ірраціональним рівнянням
та методом його розв’язування.
- піднесення до степеня;
- заміна змінної;
- розкладання на множники;
- оцінка ОДЗ;
- графічний.
|
Рівняння |
Методи розв’язування |
||||
|
A |
B |
C |
D |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
|
|
|
|
|
4) |
|
|
|
|
|
|
5) |
|
|
|
|
|
Виконайте взаємоперевірку/самоперевірку.
Варіант 1
|
|
A |
B |
C |
D |
E |
|
1 |
|
+ |
|
|
|
|
2 |
|
|
+ |
|
|
|
3 |
+ |
|
|
|
|
|
4 |
|
|
|
|
+ |
|
5 |
|
|
|
+ |
|
Варіант 2
|
|
A |
B |
C |
D |
E |
|
1 |
+ |
|
|
|
|
|
2 |
|
+ |
|
|
|
|
3 |
|
|
|
+ |
|
|
4 |
|
|
|
|
+ |
|
5 |
|
|
+ |
|
|
Крім розглянутих методів існують і інші методи розв’язування ірраціональних рівнянь. Пропоную сьогодні розглянути метод оцінки.
Метод оцінки
Цей спосіб можна застосувати в тому випадку, якщо підкореневий вираз - квадратний тричлен, який не розкладається на лінійні множники. Тому треба оцінити ліву і праву частину рівняння.
Приклад 1. ![]()
Оцінимо обидві частини рівняння:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Отже, рівність можлива коли і права, і ліва частини рівняння одночасно дорівнюють 5. Тоді справедлива така система:
![]()
![]()
![]()
Перевіркою встановлюємо, що число -1 є коренем першого рівняння.
Відповідь: -1.
Завдання 5. Розв’яжіть рівняння:
![]()
![]()
![]()
![]()
Завдання 6. Самостійна робота
Учні розв’язують рівняння у зошитах.
Варіант 1
№1. Розв’яжіть рівняння ![]()
№2. Розв’яжіть рівняння ![]() і вкажіть найменший корінь
і вкажіть найменший корінь
№3. Розв’яжіть рівняння ![]()
![]()
Варіант 2
№1. Розв’яжіть рівняння ![]() .
.
№2. Розв’яжіть рівняння ![]()
№3. Розв’яжіть рівняння ![]()
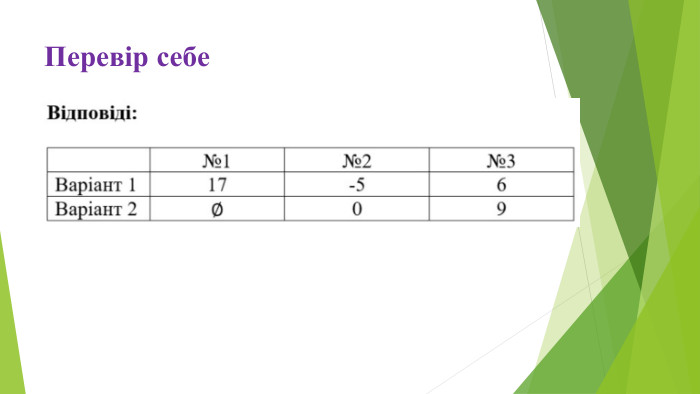
Увага на екран! Перевірте свої розв’язки.
Відповіді:
|
|
№1 |
№2 |
№3 |
|
Варіант 1 |
17 |
-5 |
6 |
|
Варіант 2 |
|
0 |
9 |
V. Підведення підсумків. Оцінювання діяльності учнів
Рефлексія
- Важким для тебе був матеріал уроку?______________________________
- На якому етапі було найважче? _____________________________________
- На якому етапі було найлегше? _____________________________________
- Що ного ти дізнався/дізналася на уроці? Чому навчися/навчилася?_______
_____________________________________________________________________________________________________________________________________________________________________________________________
- Як емоційно ти відчував себе на уроці?_____________________________
Для домашньої роботи пропонуються рівняння:

V. Притча:
Ішов Мудрець, а назустріч йому три чоловіки, які везли під гарячим сонцем візки з камінням для будівництва. Мудрець зупинився і задав кожному запитання. У першого запитав «Що ти робив цілий день?». І той відповів, що цілий день возив це важке каміння. У другого запитав мудрець «А що ти робив цілий день?», і той відповів: «А я добросовісно виконував свою роботу». А третій посміхнувся, його обличчя засвітилося радістю і задоволенням: «А я приймав участь у будівництві храму!»
І ми сьогодні на уроці приймали участь у будівництві храму – храму науки.
Бажаю всім ще кращих результатів. Дякую за роботу!


про публікацію авторської розробки
Додати розробку