конспект учня на час карантину- узагальнення і систематизація знань з теми "Множення та ділення раціональних чисел"

Число за рокладом

Класна робота

Підготовка до контрольної роботи

1. Виконайте дії:

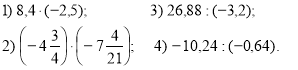
Розв’язання

1. самостійно (д.з);
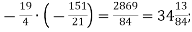2. = (спочатку перетворити у неправильний дріб)
3. = 268,8:(- 32) = 268,8  -32         = -8,4

                           256       8,4

                             128

                             128

                                 0

4. самостійно(д.з) (спочатку перенести кому)        

№2 Спростіть вираз:

Розв’язання

1. = -5,2 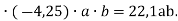(обчислення робити в стовпчик)        
2. самостійно (д.з)
3. = a – 18 – a – a – 30 = – a – 48. (спочатку розкрити дужки та звести подібні доданки)
4. самостійно (д.з)

2. Знайдіть значення виразу:

Розв’язання

1. 3, 91 : (-2,3) = 39,1: (-23) = - 1,7 (обчислення робити в стовпчик)   
2. – 2,3 – (–1,7) = – 2,3 + 1,7 = – 0,6

3,4,5 дію зробити самостійно   

3. Спростіть вираз і обчисліть його значення:

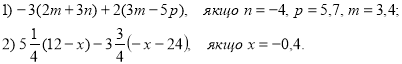
Розв’язання

1. – 6m – 9n + 6m – 10p =  – 9n – 10 p.

Якщо p = 5,7 і n = – 4, то  – 9n – 10 p = –9

Відповідь:

2. самостійно (д.з)

4. Розв’яжіть рівняння :

1)

2)

Розв’язання

1)

0,3х – 0,6 – 0,2х – 0,8 = - 2,9 (розкриваємо дужки, враховуючи знак перед ними)

3х – 6 – 2х – 8 = - 29 (домножуємо рівняння на 10, щоб позбутися десяткових дробів)

х – 14 = - 29 ( зводимо подібні доданки)

х = -29 + 14

х = - 15

2)самостійно (д.з)

№5.

Двоє робітників виготовили 330 однакових деталей. Одному з них до виконання норми потрібно зробити ще 6% деталей, а другий перевиконав норму на 26%. Скільки деталей виконав кожен з них?

Розв’язання

1 робітник - ? деталей, на 6 %

2 робітник - ?деталей, на 26 %

Переведемо відсотки в десяткові дроби.

Нехай х деталей – це норма, яку повинні виготовити робітники.

 х – 100%

1 робітник виготовив : 100% - 6% = 94%

2 робітник виготовив : 100% + 26% = 126%

Переведемо відсотки в десяткові дроби.

94% = 0,94 і 126% = 1,26.

Отже 1 робітник виготовив 0,94х деталей, 2 робітник – 1,26х, а разом 330 деталей. Маємо рівняння

0,94х + 1,26х = 330

2,2х=330

х=330:2,2 (переносимо кому)

х=3300:22

х = 150 (деталей) – норма.

1. 0,94х = 0,94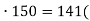деталей) – виготовив 1 робітник
2. 1,26х = 1,26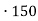= 189 (деталей) – виготовив 2 робітник

Відповідь: 141 і 189 деталей.

№6.(самостійно (д.з))

Два поїзди йшли з однаковою швидкістю, до того ж один із них був у дорозі 8 год., другий – 5 год. Яку відстань пройшов кожен поїзд, якщо другий пройшов на 171 км менше першого.

Підготуватися до к.р