Конспект уроку 2 з алгебри на тему: "Числові нерівності. Доведення числових нерівностей."

УРОК 2

Тема. Числові нерівності. Доведення числових нерівностей.

 Цілі: удосконалити вміння учнів застосовувати поняття числової нерівності до розв’язування задач, зокрема доведення числових нерівностей; розвивати навчальні інтереси, здібності на основі розумових дій; виховувати культуру математичних міркувань, уміння тактовно висловлювати свою думку.

Тип уроку: удосконалення знань і вмінь.

Хід уроку

Найважливіше — не те велике,

до чого додумалися інші,

а те маленьке,

до чого дійшов ти сам.

Харукі Муракамі

Організаційний етап

Усміхніться один одному, подумки побажайте успіхів на цілий день. Для того, щоб впоратися на уроці із завданнями, будьте старанними і слухняними. Завдання наші такі:

Не просто слухати, а чути.

Не просто дивитися, а бачити.

Не просто відповідати, а міркувати.

Дружно і плідно працювати.

 (Робота з епіграфом. Прочитайте епіграф. Як ви розумієте ці слова? (Відповіді учнів.)

Перевірка домашнього завдання

  Взаємна перевірка домашніх робіт учнями у своїх сусідів по парті й інших однокласників. Відтворення на дошці одним учнем свого варіанта розв'язку домашньої роботи (у цей час клас виконує інші завдання: повторення усних правил, перевірка інших завдань, розминка тощо) з наступною перевіркою кожним учнем своєї роботи з перевіреним зразком.

Мотивація навчальної діяльності

Розглянемо таку задачу. Дівчинка  має подарунковий сертифікат вартістю 450 грн для придбання солодощів. 1) Яку найбільшу кількість шоколадок за ціною 68 грн може купити дівчинка? 2) Чи можна за цей сертифікат придбати 22 круасани, якщо ціна одного круасана на 60 % менша, ніж ціна однієї шоколадки?

 Актуалізація опорних знань

Гра «Вірю – не вірю».

Вчитель ставить запитання:

Чи вірите ви, що…

1 Два вирази, які з’єднані між собою знаками <,>,≤,≥, називають нерівностями.

2 Нерівність 0,5>5 правильна.

3 Нерівність 2≤2 неправильна.

4 Нерівність 7>-4 строга.

5 Нерівність 6>=-13 строга.

6 Якщо х-у=-3 то х>у.

7 Якщо а-в=0 то а=в.

8 Нерівність задовольняє число 1.

9 Чи вірите, що нерівність доведена правильно:

10 Чи вірите, що знаки відношень першими почали використовувати англійські математики: знаки “>” і “<” – Томас Гарріот (1560-1621), знак «=» - Роберт Рекорд (1510-1587).

11 Квадрат будь-якого числа завжди менший від нуля.

12 Квадрат суми двох виразів дорівнює квадрату першого виразу, плюс подвоєний добуток першого на другий і плюс квадрат другого виразу.

Удосконалення знань і вмінь

Доведення нерівностей

  Приклад 1 Доведіть нерівність: , якщо а > 0; b > 0. 

Доведення: Знайдемо різницю лівої та правої частин нерівності:

.

Оскільки а > 0, b > 0, то ab > 0. Оскільки (a – b)2 ≥ 0, то ,

отже, нерівність  доведена.

Сума додатних взаємно обернених чисел не менша за 2.

Зауваження: рівність має місце при а = b.

  Приклад 2 Доведіть нерівність (m-2)²>-m(4 -m), де m — будь-яке дійсне число. 

Доведення: Утворимо різницю лівої та правої частин нерівності й спростимо її. (m-2)² -(-m(4 - m)) =  m² -4m+ 4 + 4m-m² = 4. Проаналізуємо знак результату. Оскільки, 4 > 0, різниця додатна, то ліва частина нерівності більша за праву (m-2)² > -m(4 -m) для будь-якого m. Нерівність доведено.

   Приклад 3. Доведіть нерівність, якщо x - довільне дійсне число: 16x²≥8x −1.

Доведення: Розглянемо різницю лівої і правої частини нерівності і перетворимо її. 16x²-8x +1=(4х-1)²≥0 отже, нерівність правильна для будь-якого х.

  Приклад 4. Доведіть нерівність, якщо a і b — невід’ємні дійсні числа:

.

Доведення: Домножимо обидві частини нерівності на 2: .

Внесемо число 2 під знак кореня . є середнім арифметичним чисел а і 4b, тому за доведеною нерівністю Коші ця величина не менша за середнє геометричне цих чисел тобто

   Приклад 5. Доведіть нерівність .

 Доведення: Подамо вираз  у вигляді . Отже,  є середнім арифметичним чисел b² + 4 і 1, b² + 4  1, тому за доведеною нерівністю Коші ця величина більша за середнє геометричне цих чисел,

тобто або .

Приклад 6.  Нехай х – це кількість шоколадок, тоді 98х≤450 модель зад

Робота в групах.

Доведіть нерівність, якщо x — довільне дійсне число:

1) x² + 9≥6x;    2) x² +25≥10x;    3) 4x² ≥12x −9.

Доведіть нерівність, якщо число a≥0:

   1) a +1≥2 ;   2) a + 4≥4 ;     3) a +9≥6.

Доведіть нерівність, якщо m — довільне дійсне число:

   1) m(m−4) ≥-4 ;    2) n(n+6)+9≥0;  3) (m−3)(m +5)>m(m+2)−17;

Яка з рівностей є правильною?                                      

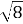1.   |4- | = -  4        2) |4- 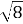| =  4-  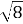      3) |5- | = 5-.

Задача «Подорож закарпаттям»

   Родина з чотирьох осіб вирішила здійснити туристичну подорож Закарпаттям. У таблиці наведено вартість п’ятиденного туру (на одну особу) та вартість проїзду в обидва кінці (для чотирьох осіб), які запропонували родині три туристичні фірми.

Скільки коштуватиме подорож для всієї родини, якщо скористатися послугами: 1) турфірми А; 2) турфірми B; 3) турфірми C?

Послугами якої турфірми необхідно скористатися, якщо на всю подорож планується витратити не більше ніж 20 000 грн?

Скільки коштуватиме найдорожчий тур (з урахуванням вартості проїзду) для всієї родини?

Рефлексія

Продовжіть фразу

-Мені було цікаво... -Ми сьогодні розібралися... -Я сьогодні зрозумів, що...

- Мені було важко... -Завтра я хочу на уроці…

Домашнє завдання за підручником____________

1.   Вивчити схему доведення нерівностей, розглянутих на уроці.

2.   Розв'язати вправи: на доведення нерівностей, подібних до розглянутих на уроці.

Доведіть, що сума квадратів двох довільних дійсних чисел не

менша від їх подвоєного добутку.