Урок алгебри в 7 класі

 

Тема. Способи задання функції

 

Мета: навчити учнів називати та ілюструвати на прикладах способи задання функції; сформувати вміння знаходити значення функції за заданим значенням аргумента і навпаки.

 

Зможете:   

-         знаходити значення функції за заданим значенням аргумента;

-         знаходити аргумент за заданим значенням функції;

-         задавати функцію за допомогою формули;

-         задавати функцію табличним способом;

-         задавати функцію графічним способом;

-         задавати функцію описом;

-         визначати спосіб задання функції і розуміти його недоліки та переваги.

Обладнання: проектор, ноутбук.

Тип уроку: комбінований

 

Хід уроку

І Організаційний етап

ІІ Перевірка домашнього завдання

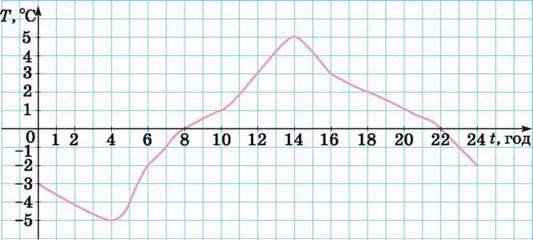
На     екрані:       графік         залежності зміни          температури        повітря       від          часу спостереження.

 

Завдання: визначте

1)    протягом скількох годин відбувалося потепління;

2)    якою була температура повітря на початку спостереження;

3)    на скільки градусів потеплішало за перші 5 годин;

4)    через скільки годин після початку спостереження температура повітря вдруге дорівнювала 3 градуси.

 

 

Завдання.  Знайдіть закономірність і запишіть відповідь.

Відстань між містами дорівнює 600 кілометрів. Автомобіль має подолати її за t годин. 

 Відповідь:  V  

Відстань між містами 800 кілометрів. Автомобіль має подолати її за t годин.

Відповідь: ?

(Самоперевірка за готовими відповідями, заздалегідь підготовленими вчителем).

 

Мотивація навчальної діяльності

Ви вже знаєте, що функцію можна задати формулою. Чи єдиний це спосіб задання функції? Відповідь: ні. Існують й інші способи  задання функції. 

Завдання уроку: ознайомитись зі способами задання функції, навчитись знаходити значення функції за значенням її аргумента

 

 

Актуалізація опорних знань

Знаємо: 

-         яке правило називають функцією;

-         яку залежність однієї змінної від другої називають функціональною;

-         як читають y = f(x);

-         що називають аргументом функції;

-         що таке область визначення функції;

-         що називають значенням функції; - що таке область значень функції; - що означає запис f(a) = b.

Хочемо дізнатись: 

про переваги й недоліки різних способів задання функції.

Функцію вважають заданою, якщо вказано правило, за допомогою якого можна за кожним значенням незалежної змінної знайти значення залежної змінної.

Функцію можна задати: описом, формулою, таблицею, графічно.

Найчастіше функції задають формулою або графічно.

Якщо функцію задано формулою, то за поданими значеннями аргумента можна знайти значення функції ( і навпаки), підставивши відповідні значення у формулу, якою задано функцію. Формування компетентностей

Ø Виконання усних вправ

1.Прочитайте записи, укажіть аргумент функції та залежну змінну:

а) f (5)= 12;           b) f(1) = -3;        в) f(0) = 1.

2. Функцію задано формулою y = 3x – 5. Знайдіть значення функції, якщо значення аргумента дорівнює: 0; -2; 15.

 

Ø Колективне виконання завдань під керівництвом учителя

1.     Функцію задано формулою f(x) = 2x – 4. Знайдіть: .

2.     Функцію задано формулою f(x) = 2𝑥²– 5. Заповніть таблицю:

X	-2	-1	0	1	2
Y
Функцію задано таблицею:
X	-2	-1	0	1	2
Y	-15	-9	7	9	15

3.

 

Знайдіть:

а) f(0) + f (2);                                    в) f(-2) + f(2);

б) f(-2) -  f (1);                                   г) f (-1) + f (0).

Чи можна знайти значення цієї функції при x = -4; -3; 3?

4.Задайте формулою функцію, задану описово, якщо:

а) значення функції на 1більше, ніж значення аргументу;

б) значення функції дорівнюють подвоєним значенням аргументу;

в) значення функції утричі менше від значень аргументу.

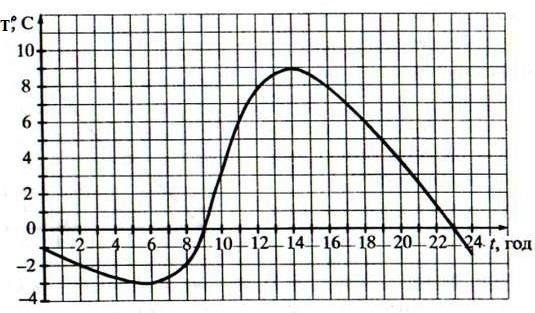
5.Функцію задано графіком (на екрані). Знайдіть значення функції при t = 6; 8; 14; 17; 23.

При яких значеннях аргумента значення функції дорівнює нулю?

 

 

6. Робота з підручником [1]: розглянути приклади 4 та 5;

№ 896; 900.

 

 

Підсумки кроку

 

Які способи задання функції ви знаєте?

У чому полягає:

1 )табличний;

2)  графічний;

3)  описовий способи задання функції?

Чи можна одну й ту саму функцію задати різними способами?

Який спосіб задання функції, на вашу думку найзручніший?

Вислухати думки учнів та проаналізувати. 

Слід пам’ятати, табличний спосіб задання функції має істотний недолік, оскільки не дає повного уявлення про характер функціональної залежності між аргументом і функцією та не є наочним. Найчастіше табличним способом задання функції користуються в медицині, біології при експериментальних дослідженнях.

 Основними недоліками словесного способу задання функції є неможливість обчислення значень функції при довільному значенні аргумента і відсутність наочності. Головна перевага полягає в можливості задання тих функцій, які не можна виразити за допомогою формули. 

Перевагою графічного способу задання є наочність, що дозволяє встановити важливі особливості поведінки функції. Недолік графічного способу полягає в неможливості  детального дослідження функції. В математиці найчастіше використовується саме  спосіб задання функції за допомогою формули. Перевагами цього способу є компактність, можливість підрахунку значення функції при будь-якому значенні аргумента і можливість з більш детального дослідження поведінки функції. Однак аналітичному способу задання функції властива недостатня наочність і можлива складність обчислення значень функції.

Розгляд різних способів задання функції показує, що для докладного вивчення її поведінки найкраще поєднувати спосіб задання функції за допомогою формули з побудовою її графіка, тобто одночасно використовувати аналітичний і графічний.

 

Домашнє завдання

[1]: п. 21, приклади 1-5, № 881, 883, 887, 890 Бонус

Функцію задано формулою: f(x) = 𝑥³ +2x Знайдіть: f(6); f(-5); f(0).

 

 

Література

1.     А.Г. Мерзляк , В.Б .Полонський, М.С. Якір Алгебра. Підручник для 7 класу загальноосвітніх навчальних закладів. Х.: «Гімназія», 2020. – 288 с.

2.     Програма «Математика. 5-11 класи: навчальні програми, методичні рекомендації щодо організації навчально-виховного процесу в 2018/2019 навчальному році/ Укладач Р.В. Гладковський. – Харків: Видавництво «Ранок», 2018. – 224 с.