Види та побудова перерізів многогранників.
Про матеріал
Урок __________ ГЕОМЕТРІЯ 11 клас
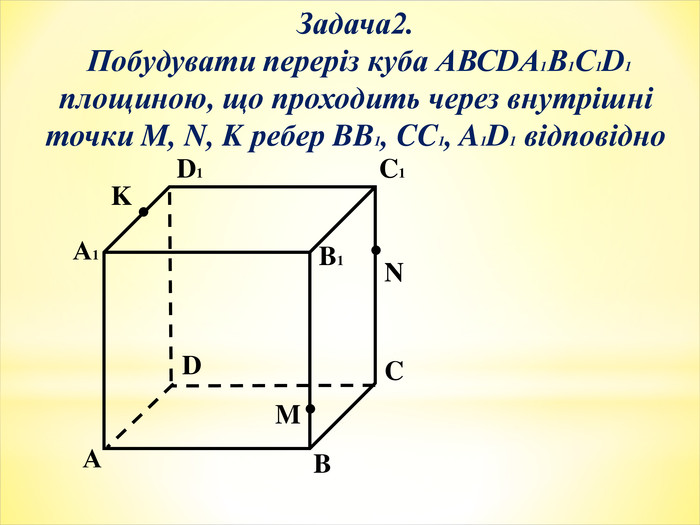
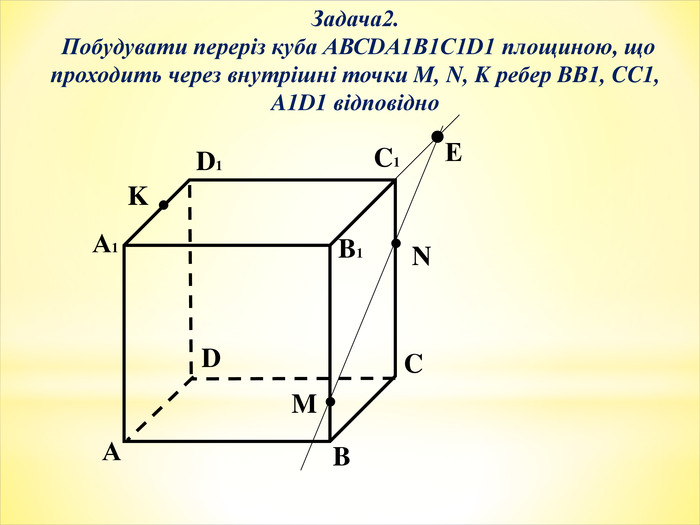
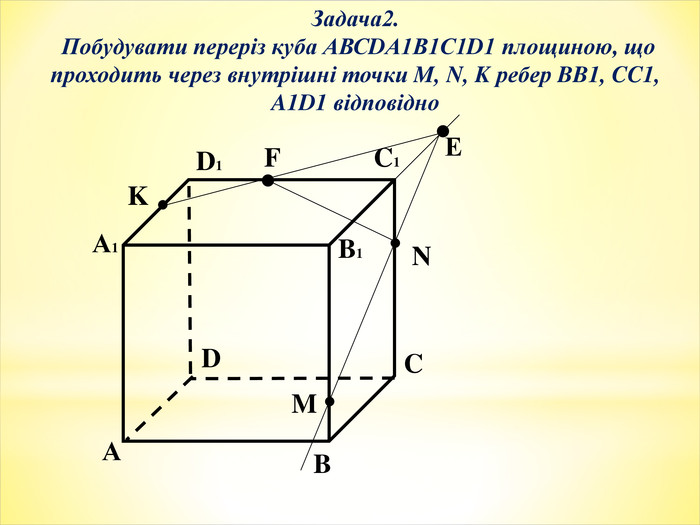
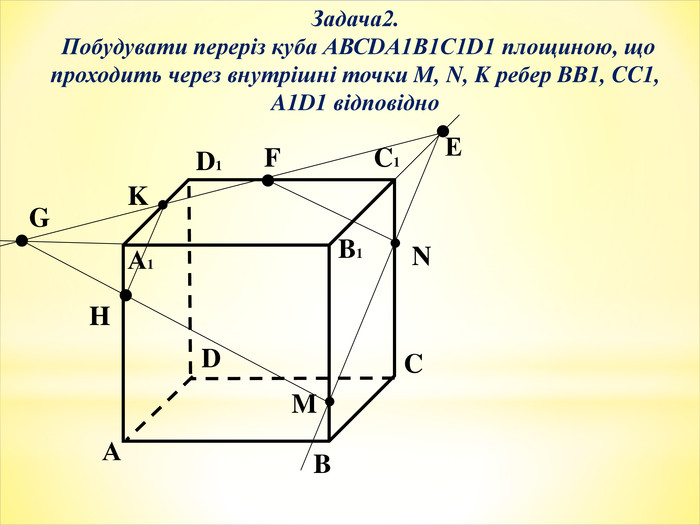
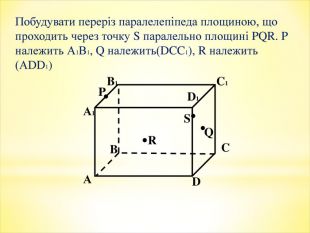
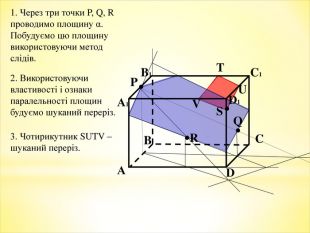
Тема уроку: Зображення призми і побудова її перерізів.
Тип уроку:урок засвоєння нових знань.
Мета уроку: формування понять переріз, діагональний переріз призми, а також умінь будувати перерізи призм. Ознайомлення з методами побудови перерізів. Розвиток просторової уяви, навичок креслення, логічного та самостійного мислення.
Обладнання: моделі призм. Мультимедійний проектор.
Перегляд файлу
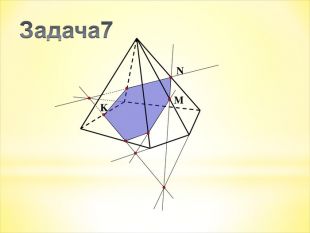
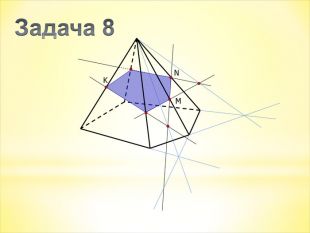
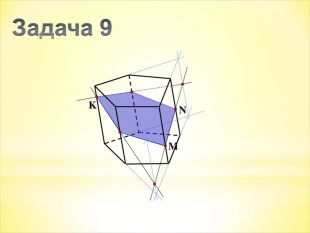
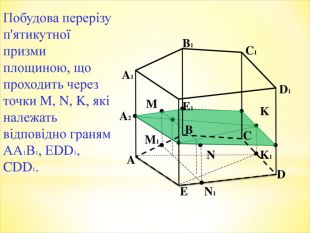
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


















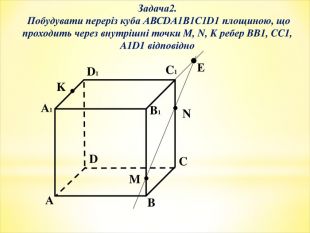
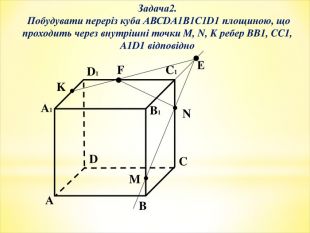
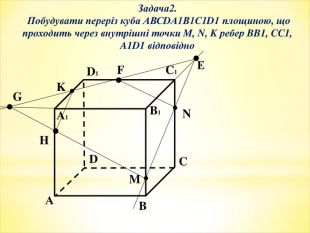
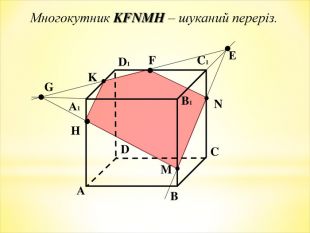







-
Нестерчук Людмила Олександрівна
03.10.2024 в 10:21
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пономарьова Раіса Іванівна
04.10.2022 в 09:17
Дякую! Дуже корисна та змістовна презентація.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Перепелиця Тетяна Іванівна
23.11.2021 в 21:54
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Велитченко Елена
19.10.2021 в 21:34
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук