Конспект уроку на тему: "Розв’язування систем двох лінійних рівнянь з двома змінними графічним способом."
удосконалити вміння учнів розв'язувати системи рівнянь із двома змінними та графічний спосіб розв'язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв'язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, розв'язувати систему двох лінійних рівнянь графічним способом; розвивати увагу, логічне мислення, пам'ять, формувати вміння грамотно формулювати власні думки.
Тема: Розв’язування систем двох лінійних рівнянь з двома змінними графічним способом. Самостійна робота №7
Мета: удосконалити вміння учнів розв’язувати системи рівнянь із двома змінними та графічний спосіб розв’язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв’язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, розв’язувати систему двох лінійних рівнянь графічним способом; розвивати увагу, логічне мислення, пам'ять, формувати вміння грамотно формулювати власні думки.
Тип уроку: удосконалення вмінь і навичок.
Обладнання: Алгебра. Підручник для 7 класу. набір демонстраційного креслярського приладдя, картки для самостійної роботи.
Хід уроку
I. Організаційний момент.
Повідомляємо учням місце уроку в темі, перевіряємо готовність до уроку.
II. Перевірка домашнього завдання.
Самоперевірка за готовими розв’язаннями. Декілька учнів записують на дошці розв’язання вправ домашнього завдання. Решта учнів здійснюють самоперевірку, беруть участь в обговоренні завдань, відповідають на запитання вчителя. Можна виконати перевірку не всіх завдань, а лише тих, які викликали в учнів труднощі
IV. Актуалізація опорних знань
Запитання до класу
1. Що називається системою рівнянь? (слайд 2) Системою рівнянь називаються два або декілька рівнянь у яких потрібно знайти всі спільні розв’язки
2. Як записуються системи рівнянь? Стовпчиком і об’єднуються фігурною дужкою
3. Що означає розв’язати систему рівнянь? Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що розв’язків не має.
4. Для розв’язування системи лінійних рівнянь з двома змінними, можна користуватися графіками рівнянь. Такий спосіб називається графічним способом розв’язування систем
Тестові завдання
Варіант 1
- Яка з наведених пар чисел є розв’язком рівняння 12х-7у=1?
А. (3;5) Б. (3;-5) В. (5; 3) Г. (5; -3)
2. Укажіть рівняння графік якого зображений на рис.1
А. х+2у=2 Б. 2х +у=2 В. х-2у=2 Г. 2х -у=2
Варіант 2
- Яка з наведених пар чисел є розв’язком рівняння 15х-8у=4?
А. (4;-7) Б. (4;7) В. (7;4) Г. (7;-4)
2. Укажіть рівняння графік якого зображений на рис.2
А. х+2у=4 Б. 2х +у=2 В. х-2у=4 Г. 2х -у=2
Самоперевірка з готовими відповідями
Відповіді : Варіант 1. 1-А. 2 - В
Варіант 2. 1-Б. 2-А
Фронтальна робота
- Переконайтеся, що пара чисел (3;2) є розв’язком рівняння: 2х- у=4
- Побудуйте в одній системі координат графіки рівнянь 2х-у=6 і 4х-3у=12 і знайдіть координати точок їх перетину.
III. Формулювання мети і завдань уроку. (слайд 5)
Система рівнянь
Ми сьогодні продовжуєм
вивчати цю тему.
Це, бачите два рівняння,
А це - їх система.
Ці рівняння як в тандемі,
Удвох – дружка з дружкою,
їх з’єднують у систему
Фігурною дужкою.
В цих рівнянь – ті самі змінні,
Ті самі їх значення.
Чим такі системи цінні,
Скоро ми побачимо.
Так відомий автор підручників із математики в поетичній формі розповів нам, що ми вивчатимемо сьогодні на уроці. Отже, завдання нашого уроку: продовжувати знаходити розв’язки систем двох лінійних рівнянь із двома змінними за допомогою графічного способу розв’язування рівнянь.
V. Удосконаленння вмінь і навичок
Колективне виконання завдань під керівництвом вчителя
Виконання усних вправ
Розв’язування задач №1053(усно),. Якщо ці прямі не перетинаються, то система має єдиний розв’язок; якщо прямі не перетинаються (паралельні), то система розв’язків не має; якщо прямі збігаються, то система має безліч розв’язків.
Виконання письмових вправ
Алгоритм розв’язання систем двох лінійних рівнянь графічним способом
1) побудувати графіки рівнянь на одній координатній площині;
2) знайти координати точки перетину графіків або впевнитись в тому, що графіки рівнянь не перетинаються (є паралельними) або збігаються;
3) якщо координати точки перетину ‒ цілі числа, то виконати перевірку; якщо ні, то розв’язок системи визначити наближено;
4) дати відповідь.
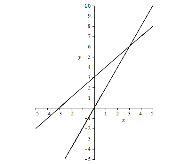 1)
1) ![]() (слайди 16-18)
(слайди 16-18)
|
x |
0 |
2 |
|
y |
0 |
4 |
|
x |
0 |
-3 |
|
y |
3 |
0 |
![]()
![]()
Графіки функцій перетинаються в точці ![]()
Виконаємо перевірку : ![]()
Відповідь: (3;6).
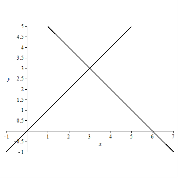 2)
2) ![]() (слайди 21,22)
(слайди 21,22)
![]()
![]()
|
x |
0 |
1 |
|
y |
0 |
1 |
|
x |
2 |
6 |
|
y |
4 |
0 |
Графіки функцій перетинаються в точці ![]()
Виконаємо перевірку![]()
![]()
3) ![]() (слайди 27, 28)
(слайди 27, 28)
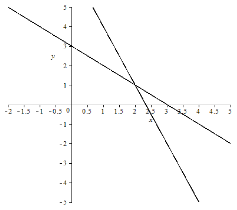
![]()
![]()
|
x |
0 |
3 |
|
y |
3 |
0 |
|
x |
1 |
2 |
|
y |
4 |
1 |
Графіки функції перетинаються в точці ![]()
Виконаємо перевірку: ![]()
Самостійна робота №7
Варіант 1 Варіант 2
1. Розв’яжіть графічно системи рівнянь 1. Розв’яжіть графічно системи рівнянь
1) ![]() 1)
1) ![]()
2) ![]() 2)
2) ![]()
3) ![]() 3 )
3 ) ![]()
2. Скільки розв’язків має система рівнянь 2. Скільки розв’язків має система рівнянь
1) ![]() 1)
1) ![]()
VII. Домашнє завдання. Опрацювати § 26 №1067, 1059


про публікацію авторської розробки
Додати розробку
