Урок алгебри 7 клас "Графічний спосіб розвязування систем рівнянь"

 

Тема  Графічний спосіб розв’язування систем лінійних рівнянь із двома змінними.

Мета навчальна: формування в учнів навичок і вмінь розв’язувати системи лінійних    рівнянь графічним методом; визначати кількість розв’язків системи рівнянь, не будуючи графіків

розвиваюча: розвивати самостійність, уміння логічно мислити

 виховна: виховувати вміння працювати в групах, охайність, чесність, акуратність раціонально використовувати час при виконанні завдань.

Тип уроку: урок-гра  

                                           Сміливість розуму характерна для всіх математиків.

                                            Математик не любить, коли йому про щось   

                                            Розповідають, він сам хоче дійти до всього.

                                                                                                            І.Сойер.

Хід уроку

Учитель  Сьогодні на уроці ми продовжимо вивчати тему « Розв’язування систем лінійних рівнянь з двома змінними графічним способом». Урок проведемо нетрадиційно: запрошую вас у цікаве плавання по математичному морю.

Щоб воно було успішним, потрібен досвідчений капітан. Ви, напевне, не будете заперечувати, щоб ним була я. На правах капітана ознайомлю вас з картою маршруту.(показати на карті)

Почнемо подорож із Рідної Гавані. Які її координати?

 ( очікувана відповідь: (0;0)). Далі повернемо у порт Будівельник. Які його координати? ( очікувана відповідь: (-12;8)). Відвідаємо незвичну країну Нові Знання, яка знаходиться на острові з такою самою назвою. Які координати її столиці? ( очікувана відповідь: (-4;15)). Далі прямуватимемо до загадкової країни Розумова Розминка. Назвіть координати її головного міста

( очікувана відповідь: (-6;12)).

Остання зупинка – Королівство Таємничих  чисел. Але нам треба бути особливо обережними бо саме на цьому етапі подорожі зустрічаються айсберги.

Під час подорожі вам доведеться показати свої знання, бути уважними, старанними, не хвилюватись, щоб вчасно повернутися до Рідної Гавані.

Спочатку перевіримо вашу готовність до такої подорожі. Для цього виконаємо завдання (двоє учнів працюють біля дошки).

Завдання

1. Розв’язати графічно систему рівнянь

 

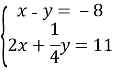
 Відповідь:  (4; 12)

Чи є пара чисел (7; 18) розв’язком системи:

 
           

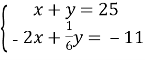
Відповідь : Так

Учитель  Будь яка подія в житті людини чи людства в цілому відбувається певного числа, місяця та року. Чи знаєте ви, на яку подію вказують дві пари чисел, що є розв’язками даних систем?

Відправляємось у подорож на вітрильнику  «7-Б клас»

( очікувана відповідь: (7;18) – кількість учнів у 7 класі, а (4;12) – дата сьогоднішнього уроку.

Зручно розміщуємось у каютах вітрильника. На партах є завдання, які записано на картці перепустці, та який екіпаж повинен розв’язати, щоб нас прийняв п. Будівельник.

 

Картка – перепустка до п. Будівельник

Розв’язати графічно систему рівнянь

Учитель Ми  дібралися до п.Будівельник. Що там лише не будують: кола, піраміди, призми та різні многокутники! І всі будівельники мають якийсь інструмент: циркуль, лінійку, олівець. Будівельники приготували нам завдання.

Завдання від будівельників

1. Що означає розв’язати систему рівнянь?
2. Що називається розв’язком системи рівнянь?
3. Які системи доцільно розв’язувати графічно?

 

Учитель Розв’яжемо завдання, що є перепусткою до країни Нові Знання.

(Двоє учнів працюють біля дошки).

Завдання

Розв’язати графічно систему рівнянь:

а)  б)
                                                  
 

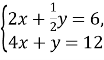
Учитель Як ви думаєте: чи можна що не будь сказати про кількість розв’язків системи лінійних рівнянь, не розв’язуючи її? Можливо є зв'язок між розв’язками системи та коефіцієнтами  при невідомих і вільних членах.

Запишемо відношення коефіцієнтів при однакових невідомих і вільних членах рівнянь двох останніх систем:

 

1)  2)
                                                  

   Який висновок можна зробити? (Учні роблять висновок)

Учитель Ми потрапили до незвичайної країни Нові Знання. Тут ніхто не сидить без діла. Декому доводиться працювати і ночами. І всі жителі мають дивний зв'язок із математиками минулого. Від них вам картка для гостей з теоретичними відомостями, що стосуються розв’язування системи лінійних рівнянь.

                                                                                  ( на дошці плакат)

 

Картка для гостей

Розглянемо систему  
 

 

якщо, то система має безліч розв’язків

 

якщо , то система  не має  розв’язків

 

якщо , то система має єдиний розв’язок

 

Учитель Це є підтвердженням нашого висновку.

А ми прибули до загадкової країни Розумова Розминка. Жителі цієї країни дуже люблять різні головоломки, загадки, а також ставити один одному запитання й одразу на них відповідати.

Вони і нам підготували сюрприз-завдання, яке слід відразу виконати.

 

Сюрприз-завдання

З’ясуйте, чи має система розв’язки і скільки:

а
                   Відповідь: Один

 

б
               Відповідь: Безліч

 

в)
                   Відповідь: Немає розв’язків

Учитель  Наш вітрильник тримає курс на Королівство Таємничих Чисел. Увага! До нас наближається айсберг. Читайте, яке завдання написано на ньому. Виконайте його.

Завдання

Знайди помилку в міркуваннях: «Маємо правильну числову рівність :

                           4 : 4  =  5 : 5

Винесемо за дужки в кожній частині рівності спільний множник. Одержимо:

                           4 х ( 1 : 1 )  =  5 х ( 1 : 1 )

Число в дужках рівні, тому 4 = 5 , або 2 х 2 = 5»

 ( очікувана відповідь винесення за дужки виконано неправильно).

Учитель Ми обминули небезпеку. І  наш вітрильник змінив курс і держить його на Рідну Гавань.

Ми вже бачимо, як мерехтить маяк Рідної Гавані. Перевіримо свої сили та з’ясуємо,  чи можемо доплисти до неї. А ось і човни з рятівними кругами. До човнів і рятівних кругів прикріплено завдання – розв’язати графічно системи рівнянь.

Працюють дослідники у порядку черговості.

Перша група               Човен « Р. Декарт»

Розв’язати систему
 

Історична довідка про Р. Декарта, підготовлена учнями

Рене Декарт

•      Дата народження: 31 березня 1596
•      Місце народження:        Лає, Ендр і Луара, Франція
•      Дата смерті:       11 лютого 1650
•      Місце смерті:    Стокгольм, Швеція
•      Школа, традиція: Картезіанство, Континентальний раціоналізм
•      Період: Філософія XVII століття (Філософія Нового часу)
•      Напрям: Європейська філософія
•      Основні інтереси: метафізика, епістемологія, наука, математика
• Значні ідеї: Соgitо егgо sum, метод радикального сумніву, Декартова система координат, Картезіанський дуалізм, визнаний засновником Новоєвропейської філософії
•      Зробили вплив: Платон, Арістотель, Ансельм, Хома Аквінський, Оккам, Суарез, Мерсенн

• Послідовники: Спіноза, Арно, Мальбранш, Локк, Лейбніц, Кант Гуссерль

Цікаві факти Великий фізіолог І. П. Павлов поставив пам'ятник-бюст Декарту біля своєї лабораторії (Колтуші), тому що вважав його передвісником своїх досліджень.

31 березня 1596, Лає (провінція Турень), нині Декарт (департамент Ендр і Луара) — 11 лютого 1650, Стокгольм) — французький математик, філософ, фізик і фізіолог, творець аналітичної геометрії і сучасної символіки алгебри, автор методу радикального сумніву у філософії, механіцизму у фізиці, передвісник рефлексології.

Знамениті учні: Бессель, Фрідріх Вільгельм

Друга група               Човен « П. Ферма»

Розв’язати систему  
 

 

Історична довідка про П. Ферма, підготовлена учнями

П'єр де Ферма (фр. Ріегге dе Fегmаt, 1601—1665)

французький математик - один із творців аналітичної геометрії, математичного аналізу, теорії вірогідності і теорії чисел. По професії юрист, з 1631 року — радник парламенту в Тулузі. Блискучий поліглот. Найбільш відомий формулюванням Великої теореми Ферма.

П'єр Ферма народився 17 серпня 1601 року в гаськонськом містечку Бомон-де-Ломань (Франція). Його батько, Домінік Ферма, був заможним торговцем, другим міським консулом; мати, Клер де Лонг — викладачка математики. У сім'ї, крім П'єра, були ще один син і дві дочки. Ферма здобув юридичну освіту — спочатку в Тулузі, а потім в Бордо і Орлеані.

У 1631 році, успішно закінчивши навчання, Ферма викупив посаду королівського радника парламенту (іншими словами, члена вищого суду) в Тулузі. У цьому ж році він одружився на далекій родичці матері, Луїзі де Лонг. У них було п'ятеро дітей.

Швидке службове зростання дозволило Ферма стати членом Палати едиктів в місті Кастр (1648). Саме цій посаді він зобов'язаний додаванням до свого імені ознаки знатності — частки сіє; з того часу він стає П'єром де Ферма.

Близько 1652 року Ферма довелося спростовувати повідомлення про свою кончину під час епідемії чуми; він дійсно заразився, але вижив. У 1660 році планувалася його зустріч з Паскалем, але із-за поганого самопочуття обох учених зустріч не відбулася.

П'єр де Ферма помер 12 січня 1665 року в місті Кастр, під час виїзної сесії суду. Спочатку його поховали там же, в Кастрі, але незабаром (1675) прах перенесли в родинну усипальню Ферма, в церкві августинців (Тулуза). Старший син, Клеман-Самуель, видав посмертні збори його праць, з яких сучасники і дізналися про чудові відкриття П'єра Ферма.

Третя група               Човен « Д.Пойя»

Розв’язати систему  
 

Історична довідка про Д. Пойя, підготовлена учнями

«Математика цікава тоді, коли дає поживу нашій винахідливості й здатності до міркувань». Це слова математика Джорджа Пойа. Домашнім завданням було знайти інформацію про життя та діяльність Рене Декарта, П'єра Ферма, Карла Гаусса, Дьердь Пойа, Льва Толстого, Леонардо да Вінчі.

Дьйрдь Пойа.народився 13 грудня 1887, Будапешт, Австро-Угорщина, нині Угорщина — 7 вересня 1985, Пало-Алто, Каліфорнія, США) — угорський, швейцарський і американський математик.

Закінчив Будапештський університет (1912), в 1914-—1940 працював у Вищій технічній школі в Цюриху (з 1928 проф.). У 1940 переїхав в США. Основні праці по теорії чисел, функціональному аналізу, математичній статистиці (розподіл Пойа) і комбінаториці (теорема Пойа).  Живучи в США, Пойа багато працював з шкільними вчителями математики і вніс великий вклад до популяризації науки.

Він написав декілька книг про те, як люди розв'язують задачі і як треба учити розв'язувати задачі.   Пойа про аналогію:   «Можливо, не існує відкриттів ні в елементарній, ні у вищій математиці, ні навіть, мабуть, в будь-якій іншій області, які могли б бути зроблені, без аналогії».

 

Учитель. Подорож закінчилася. Чи означає це, що ви ознайомились з усією країною Математикою? Звичайно, ні . Але думаю, що ви вже розумієте, що математика – це країна, яка не має меж.

 Сміливість розуму сьогодні була характерною для … Самостійно розв’язували завдання … Допитливість … оцінюється.

 Якими словами ви хочете оцінити нашу подорож. (Очікувана відповідь: цікава, захоплююча, пізнавальна).

Системи рівнянь першого ступеня мають велике значення. До них зводиться багато задач механіки;  задач пов’язаних із складанням карт за даними геодезичних зйомок; задач атомної фізики. Такі системи розв’язують під час складання прогнозів погоди.

Удома пропоную вам виконати таке завдання

1). Прочитати § 28,

2). Знайти відповідь на запитання 1- 7 (ст. 184),

3). Розв’язати  № 945,948

Закінчую урок такими словами англійського математика Л.Морделла:       « Ніхто не піде далеко в математиці і не стане справжнім математиком, якщо не матиме деяких необхідних рис. У ньому повинні жити Віра, Надія і Допитливість, і найважливіша з цих рис – Допитливість. Він повинен раз у раз запитувати себе: чому, як і коли – і це мусить стати головним рушієм, що приводить його в дію».