Конспект уроку "Прямокутна система координат на площині. Відстань між двома точками із заданими координатами"

Урок №6. Тема:  Прямокутна система координат на площині. Відстань між двома точками із заданими координатами

Формування компетентностей:

предметна компетентність:

• допомогти повторити, узагальнити та систематизувати набуті в попередніх класах знання учнів про прямокутну систему координат на площині;
• розглянути формулу знаходженням відстані між двома точками із заданими координатами;

ключові компетентності:

• спілкування державною мовою – уміння доречно та коректно вживати в

мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку; поповнювати свій словниковий запас;

• математична компетентність – уміння оперувати числовою інформацією;
• уміння вчитися впродовж життя – уміння оцінювати результати своєї

навчальної діяльності.

Тип уроку: засвоєння вмінь та навичок.

Обладнання та наочність: підручник з геометрії за 9 клас, автори: Мерзляк, Полонський, Якір, 2017 р.

Хід уроку

I. Організаційний момент.

• Налаштовування на роботу.
• Перевірка домашнього завдання:

(§1 п.1 № 1.16, 1.20)

№ 1.16 Чому дорівнює значення виразу:

1) ;

2).

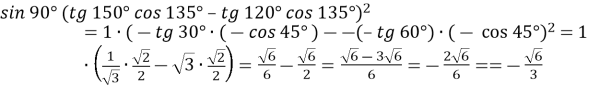№1.20. Знайдіть суму квадратів косинусів усіх кутів прямокутного трикутника.

– гострі кути прямокутного прямокутника.

.

II. Актуалізація опорних знань.

Фронтальне опитування

1. Скільки осей зазвичай зображають на координатній площині? (2)
2. Вісь ОХ називають віссю … (абсцис)
3. Друга координата точки називається … (ординатою точки)
4. Початок координат – це точка з координатами … (0;0)
5. У якій чверті лежить точка з координатами (5;-100)? (IV)
6. Точка з координатами (5;0) віддалена від початку координат на відстань … (5)

Мотивація навчальної діяльності учнів

Ми звикли знаходити відстані між точками за допомогою лінійки. А чи можна знайти відстань між точками, які лежать на координатній площині?  Тому метою сьогоднішнього уроку є вивести формулу для знаходження відстані між двома точками, заданими координатами, які не лежать на координатних осях та вчитись використовувати її для розв’язування задач.

План вивчення нового матеріалу

1. Розповідь про Рене (Картезія).
2. Прямокутна система координат.
3. Теорема про відстань між двома точками із заданими координатами.

Опорний конспект

Розповідь про Рене (Картезія) Декарта

Народився в Лае (Турень) у 1596 році. Навчався в єзуїтській колегії в Ла-Флеш (провінція Анжу), потім вивчав медицину та право. Закінчив університет в Пуатьє у 1616 році. У 1618 році познайомився з Й. Бекманом, під впливом якого зацікавився математикою та фізикою. У 1637 році написав математичний трактат «Геометрія», в якому були закладені основи аналітичної геометрії. Він стверджував, що єдиним загальним методом математики є алгебраїчний. У своїх працях від він ввів метод ортогональних координат, узагальнив поняття про координатну площину. Найвідоміший його вислів – «Я мислю – отже, я існую!»

Прямокутна система координат

Нехай задано деяку площину, наприклад, площина дошки. Проведемо у ній дві взаємно перпендикулярні прямі-осі. Точку перетину осей називають початком координат. Вона має координати (0;0). Така система координат називається прямокутною або декартовою.

Кожній точці на координатній площині можна поставити у відповідність єдину впорядковану пару чисел, і навпаки. Ця пара чисел називається координатами точки у даний системі координат.

Осі розбивають координатну площину на чотири необмежені області, які прийнято називати чвертями.

Повернемось до поставленої проблеми: яким чином можна визначити відстань від точки до початку координат?

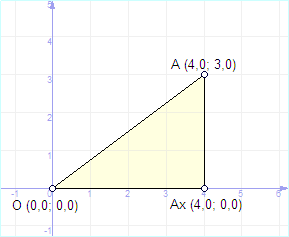Задача 1. (колективно у групах, 3+3 хв)

Дано: А(4;3)

Знайти: ОА.

Розв’язання.

Опустимо з точки А перпендикуляр на вісь абсцис. Розглянемо прямокутний Δ АА_хО. У ньому катет АА_х=3, ОА_х=4. Це випливає зі значень координат точки А. Згідно теореми Піфагора . Отже, ОА=5.

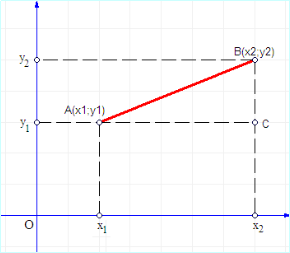
Теорема про відстань між двома точками із заданими координатами

Розглянемо, як це буде в загальному випадку. Нехай задано точки на координатній площині своїми координатами: А(х₁;у₁) і В(х₂;у₂). Для спрощення, нехай обидві точки лежать у І чверті, при чому х₁< х₂, y₁< y₂. Опустимо з кожної точки перпендикуляри на обидві осі. Розглянемо катети прямокутного Δ АСВ. Маємо, що АС= х₂- х₁, а ВС= у₂- у₁. Довжина гіпотенузи трикутника є шуканою відстанню, тому зручно використати теорему Піфагора, згідно якої , а отже, .

Ми довели теорему про відстань між двома точками із заданими координатами:

Відстань між двома точками дорівнює кореню квадратному із суми квадратів різниць їх відповідних координат.

Ми розглянули випадок, коли обидві точки лежать в І чверті, але суть доведення не змінюється, якщо точки А і В лежать в ІІ, ІІІ, IV або в різних чвертях. Спробуйте довести теорему для інших випадків вдома самостійно.

IV. Засвоєння нових знань і способів дій

№ 8.1. Знайдіть відстань між точками A і B, якщо:

1) A (10; 14), B (5; 2);            2) A (–1; 2), B (4; –3).

№ 8.3. Вершинами трикутника є точки A (–1; 3), B (5; 9), C (6; 2). Доведіть, що трикутник ABC рівнобедрений.

№ 8.4. Доведіть, що точка M (0; –1) є центром кола, описаного навколо трикутника ABC, якщо A (6; –9), B (–6; 7), C (8; 5).

№ 8.11. Доведіть, що трикутник з вершинами в точках A (2; 7), B (–1; 4) і

C (1; 2) є прямокутним.

№ 8.21. Доведіть, що чотирикутник ABCD з вершинами в точках A (–2; 8),

B (3; –3), C (6; 2) і D (1; 13) є паралелограмом.

V. Підбиття підсумків уроку, рефлексія

Чи правильно, що…

1. Відстань від точки (3;0) до точки (0;4) дорівнює 5?
2. Довжина ламаної АВС з вершинами А(0;1), В(1;1) та С(9;7) дорівнює 11?

VI. Домашнє завдання
(§3 п.8 (ст.79-80)  № 8.12, 8.20)