Конспект уроку "Рух тіла по похилій площині"

Тема: Рух тіла по похилій площині.

Мета:

• формувати вміння учнів використовувати другий закон динаміки Ньютона для опису руху тіл по похилій площині;
• розвивати уяву і мислення учнів;

•    виховувати  увагу, сміливість  під час розв’язування задач та тестових завдань,

• виховувати акуратність під час проведення експерименту.

Обладнання: міні-підручники, проектор, презентація, дидактичний матеріал.

Обладнання: дерев’яні брусок, трибометр, динамометр, штатив, набір важків,  міні-підручник.

Тип уроку: урок вивчення нового матеріалу.

ТЗН: ноутбук, відео проектор.

Наочності: 1.Міні-підручник «Рух тіла по похилій площині».

 2. Презентація «Рух по похилій площині».

 

Хід уроку:

1. Організаційний момент.

Перевірка готовності учнів до уроку. Привітання. Протягом  уроку у вас буде змога накопичувати бали, щоб отримати оцінку.

 

2. Мотивація.

Перегляд гімназичної програми «Міркувалки». (Учні перших класів)

(Ведучій: Доброго дня. Сьогодні ми з вами поміркуємо над змістом приказки «Любиш кататись, люби і санчата возить». Так що ж дорослі мають на  увазі коли кажуть «Любиш кататись, люби і санчата возить»?

Діти: …

Ведучий: Дякую за роз’яснення. Можливо у вас є запитання?

Діти: Що важче тягнути санчата по горизонтальній дорозі, підніматися на гірку, чи спускатись з неї?

Діти: Якщо я буду змагатись з татом, хто переможе?

Діти: Чому інколи щоб з’їхати з гірки треба відштовхнутись, а інколи ні?

 

3. Актуалізація опорних знань.

Сьогоднішній урок допоможе нам з вами відповісти на ці запитання. Але з початку ми пригадаємо необхідні для відповіді набуті раніше знання.

Запрошує двох учнів до дошки вони отримають індивідуальні завдання, відповіді на які вони нам пізніше продемонструють.

 

Завдання 1: Яку горизонтальну силу F треба прикласти до санчат масою m, що стоять на горизонтальній поверхні, почали рухатись з прискоренням ? Коефіцієнт тертя між санчатами і снігом дорівнює .

Завдання 2: Визначте силу F з якою людина потягнула санчата масою m за мотузку під кутом до горизонту, якщо санчата рухаються з прискоренням ? Коефіцієнт тертя санчат по снігу .  

А ми з вами всі разом пригадаємо основи динаміки:

• Які системі відліку називають інерціальними?
• Сформулюйте другий закон Ньютона?
• Як записати другий закон Ньютона, якщо на тіло діють кілька сил?
• Якою є умова рівноприскореного руху тіла?
• Сформулюйте третій закон Ньютона. Яким є його математичний запис?
• Дайте визначення сили тяжіння. За якими формулами її обчислюють і як вона напрямлена?
• Яку силу називають силою нормальної реакції опори? Як вона напрямлена?
• Дайте визначення сили тертя.

Поглянемо на розв’язки ваших товаришів.

 

4. Пояснення нового матеріалу.

Тепер ми з вами готові до розгляду головного питання. Розглянемо рух санчат вздовж похилої площини. Нехай санчата рухаються вниз. При розв’язувані даної задачи скористуємося алгоритмом який є у вас на партах.

Проаналізуємо умову і визначимо які силі діють на санчата:

– сила тяжіння;   – сила тертя;   – сила нормальної реакції опори.

Тіло збільшує свою швидкість, тому прискорення руху тіла напрямлено у напрямку руху тіла.

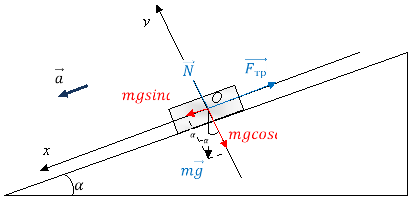Згідно нашого алгоритму наступний крок на рисунку проставити всі сили, що діють на тіло. Для економії часу в ваших міні-підручниках є готовий рисунок на якому ми з вами проставимо всі раніше названі сили. Як відомо сила тяжіння направлена вертикально вниз, реакція нормальної опори перпендикулярно до поверхні по якій рухається тіло, сила тертя у протилежний бік від напрямку руху тіла.

Пов’яжемо систему координат із тілом на поверхні Землі, вісь ОХ вздовж спуску, а вісь ОУ спрямуємо перпендикулярно до поверхні спуску.

Запишемо ІІ закон Ньютона у векторному вигляді:

Спроектуємо рівняння на осі координат:

Розв’яжемо отриману систему координат з урахуванням того, що сила тертя  прямо пропорційна силі нормальної реакції опори: .

масу можна скоротити, отже ми маємо:

Проаналізуємо отриманий вираз:

Прискорення якого набуває тіло не залежить від маси, а залежить лиже від кута нахилу і коефіцієнту опору.

За якої умови санчата не зможуть без стороннього втручання спуститись з гірки? ( Коли сила тертя буде більша за проекцію сили тяжіння на вісь ОХ тобто коли .)

Якщо , то для спуску санчат необхідно прикласти силу

 

Розглянемо рух санчат вздовж похилої площини. Нехай санчата рухаються вгору. Які сили діють в цьому випадку на санчата.

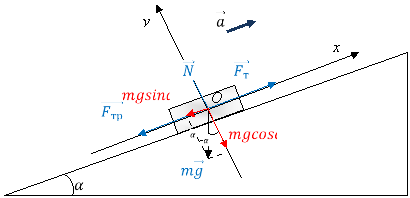
– сила тяжіння;   – сила тертя;   – сила нормальної реакції опори, .

 

 

 

 

 

 

 

Пов’яжемо систему координат із тілом на поверхні Землі, вісь ОХ вздовж спуску, а вісь ОУ спрямуємо перпендикулярно до поверхні спуску.

Запишемо ІІ закон Ньютона у векторному вигляді:

Спроектуємо рівняння на осі координат:

Розв’яжемо отриману систему координат з урахуванням того, що сила тертя  прямо пропорційна силі нормальної реакції опори: .

Отже сила, яку треба прикласти для того щоб підняти санки на гірку:

,

.

Як ми бачимо прислів’я має фізичну основу, для того щоб з’їхати на санчатах достатньо прикласти малих зусиль в порівнянні з тим щоб підняти на гірку санчата. Отже любиш кататись, люби і санчата возити.

І ще раз поглянемо на запитання які нам були поставлені на початку уроку.

Що стосується першого питання: Якщо я буду змагатись з татом, хто переможе?

Прискорення якого набуває тіло не залежить від маси, а залежить лиже від кута нахилу і коефіцієнту опору.

Чому інколи щоб з’їхати з гірки треба відштовхнутись, а інколи ні?

Коли .

Що важче тягнути санчата по горизонтальній дорозі, підніматися на гірку, чи спускатись з неї?

По горизонтальній дорозі: .

При підніманні на гірку: .

При спуску з гірки: .

 

Ми з вами навчилися розв’язувати задачі на рух тіла по похилій площині, дали відповіді на питання які поставили діти нам на початку уроку.

 

5. Закріплення вивченого матеріалу.

Шість учнів в парах працюють над експериментальним визначення коефіцієнта тертя ковзання дерев’яного бруска

Задача за експериментальними даними:

 

 

 

 

 

 

На рисунку представлені фотографія установки для дослідження ковзання  бруска по похилій площині. У центр бруска вставлено магніт. Числа на лінійці  позначають сантиметри. У момент початку руху магніт, що знаходиться в бруску, через верхній датчик включає секундомір. При проходженні магніту мимо нижнього датчика секундомір виключається. Маса бруска  50 г, кут нахилу площини α=30⁰. Знайдіть силу тертя що діє на брусок.

Як завжди розв’язування однієї задачі породжує нові. І останньої задачі ніколи не буде. Я пропоную вам попрацювати самостійно обравши для себе найбільш прийнятний для себе варіант.

Задача типу А («З видимого пізнавай невидиме». Григорій Сковорода) За наведеним шаблоном розв’яжіть аналогічну задачу, максимальний бал – 5.

Задача типу Б («Більше думай і тоді вирішуй». Григорій Сковорода) В наведеному розв’язку найдіть помилку, максимальний бал – 7.

Задача типу С (Задача повинна бути кусючою, інакше вона не буде задачею) Задачу можна віднести до високого рівня, максимальний бал – 12.

Ознайомтесь будь ласка з умовами задач, можете приступати на розв’язування вам відводиться 5 хвилин, якщо ви не встигнете зможете закінчити розв’язок дома.

 

Задача типу С

Задача повинна бути кусючою, інакше вона не буде задачею

При швидкісному спуску лижних ковзає вниз по схилу (=45°, не користуючись палками. Коефіцієнт тертя лиж по снігу  =0,1. Сила опору повітря пропорційна квадрату швидкості лижника , де- постійна величина, що дорівнює 0,7н/(м/с)². Яку максимальну швидкість може розвинути лижник, якщо його маса 70 кг?

 

 

Розв’язок.

Розглянемо рух лижника, я кий рухається вниз по схилу. На лижника будуть діяти сили: - сила тяжіння; - сила  тетря; – сила опору повітря і сила - сила нормальної реакції опори.

Запишемо основне рівняння динаміки в проекції на осі ОХ і ОУ: 

 

або

 

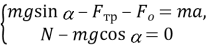
Оскільки , а , то, підставивши в систему рівнянь, отримаємо

Сила опору повітря зростає зі збільшенням швидкості лижника. Із цього випливає, що при збільшенні швидкості лижника настає такий момент, коли сума сил опору повітря і сили тертя дорівнює за абсолютною величиною проекції сили тяжіння. Тобто прискорення дорівнюватиме нулю і лижник рухатиметься з постійною швидкістю, яка матиме максимальне значення

Оскільки а=0, то рівняння (1) набуде вигляду

  =

Відповідь:

5.  Перевірка розуміння.

1. (2б)Зазначте на малюнку сили, що діють на тіло.
2. (1б)Назвіть сили, які діють на тіло?
3. (1б)Запишіть рівняння ІІ закону Ньютона у векторному вигляді?
4. (2б) Запишіть рівняння ІІ закону Ньютона у проекціях на осі координат?

Відповіді на екрані, виконайте взаємоперевірку і підрахуйте загальний бал за урок.

Карта самооцінки:

Вид діяльності	Максимальний бал	Мій бал
Бліц - опитування	4б (кожне питання 0,5б)
Задача 1	4б (біля дошки)
Робота на уроці	4б
Досліди	4б
Задача 2	4б
Задача 3	4б
Задача 4	6б
Міні-міркувалки	6б
Додаткові бали
Оцінка за урок

 

 

6. Підведення підсумків уроку.

Сьогодні на уроці ми з вами розглянули один із най розповсюджених рухів, рух по похилій площині. Дали відповіді на питання, що стояли перед нами на початку уроку.

 

7.     Домашнє завдання.

Завдання 1: Експериментальне дослідження. Виготовити динамометр, за допомогою якого дослідити залежність сили тертя від кута нахилу поверхні і побудувати графік цієї залежності.

Завдання за рівнем:

1. З вершини похилої площини висотою 10 м і кутом нахилу 300 починає зісковзувати тіло. Визначити швидкість тіла наприкінці спуску і тривалість спуску. Коефіцієнт тертя тіла об площину – 01.

2. (Б.Р.) За який час тіло, яке спочатку перебувало у спокої, зіслизне з похилої площини висотою 3 м, нахиленої під кутом 300 до горизонту, якщо при куті нахилу площини до горизонту 100 воно рухається рівномірно?

3. Санки штовхнули вгору по крижаній гірці, яка складає кут 300 з горизонтом. Санки в’їхали на певну висоту і спустились назад. Час спуску в 1,2 рази більший за час підіймання. Чому дорівнює коефіцієнт тертя?

4. Якщо нахилити дошку під кутом α до горизонту, цеглина рухається по ній практично рівномірно. За який час цеглина проїде всю дошку, якщо нахилити її під кутом β>α? Довжина дошки дорівнює l ?