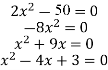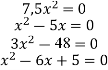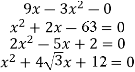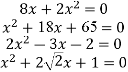Конспект уроку з алгебри для 8 класу «Розв'язання квадратних рівнянь»

Конспект уроку з алгебри

8 клас

Тема: «Квадратні рівняння»

Тип уроку: урок узагальнення та систематизації знань.

Цілі уроку:

Освітні: систематизувати знання, виробити вміння вибирати раціональний спосіб розв'язання квадратних рівнянь та створити умови контролю (самоконтролю, взаємоконтролю) засвоєння знань та умінь.

Навчити учнів прийомів усного розв'язання квадратних рівнянь.

Розвиваючі: формувати навчально-пізнавальні навички роботи з додатковим матеріалом, розвивати логічне мислення, увагу, загальнонавчальні вміння;

Виховні: виховувати інтерес до математики, активність, мобільність,  взаємодопомога, вміння спілкуватися.

План уроку:

1. Організаційний момент.
2. Цілі уроку, повторення.
3. Усна робота.
4. Математична розминка.
5. Бліц-турнир.
6. Повторення теореми Вієта.
7. Знайомство з прийомом усного розв'язання деяких квадратних рівнянь.
8. Самостійна робота.
9. Домашнє завдання.

Хід уроку:

1.Організаційний момент.

Вчитель: Сьогодні на уроці ми систематизуємо знання про методи розв'язання квадратних рівнянь, закріпимо та вдосконалимо навички розв'язання квадратних рівнянь.

2. Фронтальна робота із класом.

Усна робота

Записані рівняння:

1.         x² + 9x - 12 = 0;

2.         4×2 + 1 = 0;
3.         x² -2x + 5 = 0;
4.         2z² - 5z + 2 = 0;
5.         4y² = 1;
6.         -2x² - x + 1 = 0;
7.         x² + 8x = 0;
8.         2x²=0;
9.         -x² - 8x = 1
10.    2x + x2 - 1 = 0

4. Математична розминка.

Вчитель: Чи знаєте ви, хлопці та дівчата, що означає слово «Бліц-турнір» і з якої мови воно до нас прийшло? Для відповіді на це питання розв'яжіть рівняння і за таблицею визначте:

2x²-7x+6=0

5. Бліц-турнир.

Вчитель: Проаналізуйте висловлювання. Закресліть в таблиці літери, що позначають помилкові висловлювання (номер висловлювання збігається з порядковим номером літери). З літер, що залишилися, отримайте слово.

1. Рівняння x²+9=0 має два корені.

2.В рівнянні x²-2x+1=0 єдиний корінь.

3. У рівнянні x²-5x+3=0 сума коренів дорівнює – 5.

4. У рівнянні x²+3x=0 одне з коренів – негативне число.

5. У рівнянні x²=0 дискримінант дорівнює 0.

6. Рівняння x²-8x-3=0 немає коріння.

7. Корінням рівняння x²-100x+99=0 є числа 99 та 1.

8. Добуток коренів рівняння x²-11x+9=0 дорівнює - 9.

9. Коріння рівняння x² - 0,16 = 0 рівні 0,4.

10. Рівняння x²-9x+8=0 є неповним.

11. Якщо дискримінант рівняння – число негативне, то рівняння немає коріння.

12. Коріння рівняння x²-4х = 0 є протилежними числами.

13. Рівняння x² = 0 має один корінь.

В результаті викреслення літер має вийти: ВІДМІННО

6. Повторення теореми Вієта.

Вчитель: Скажіть, а могли б ви відразу, не проводячи обчислень, відповісти на моє запитання: «Чому дорівнює сума та добуток коріння квадратного рівняння?» (Одна людина біля дошки записує формули теореми Вієта).

Наступне завдання: усно знайти коріння рівняння з теореми:

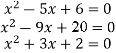  (відповіді: 3 та 2; 4 та 5; -2 та -1)

7. Ознайомлення з прийомом усного розв'язання деяких квадратних рівнянь.

Вчитель: Теорема Вієта знаходить широке застосування та в рівняннях виду aх2 + bх + с = 0.

Використання деяких властивостей дає значні переваги для швидкого отримання відповіді під час вирішення квадратних рівнянь.

Розглянемо ці характеристики:

1) a + b +с = 0;    х₁ = 1, х₂ = с/а.

5х² + 4х - 9 = 0;    х₁ = 1, х₂ = - 9/2.

2) а – b + с = 0;   х₁ = – 1, х₂ = – с/а.

Наприклад: 4х² + 11х + 7 = 0; х₁ = – 1, х₂ = – 7/4.

3) ав +с0

Усно розв'язати рівняння: х² + bх + ас = 0

Його коріння розділити на а.

а) 2х² - 11х + 5 = 0.

Вирішуємо усно рівняння: х² – 11х + 10 = 0. Його коріння 1 та 10. Ділимо на 2.

Тоді х₁ = ,   х₂ = 5.

Відповідь: ;  5.

в) 6х² -7х - 3 = 0

Вирішуємо усно рівняння: х² -7х - 18 = 0. Його коріння -2 і 9. Ділимо на 6.

Тоді х₁ = -,  х₂ =.

 Відповідь: -;  .

8. Самостійна робота.

Вчитель: Розв'яжіть рівняння, використовуючи ці властивості

Відповіді:

1 варіант 1) 1; 3/14. 2) -1; 40. 3) -1; 183/100.

2варіант 1) 1:5/13. 2) 1; -24. 3) 1-197/100.

Вчитель: Урок добігає кінця. Сьогодні ми повторили всі необхідні математичні поняття, формули та способи розв'язання квадратних рівнянь. Підсумком нашого уроку буде невелика самостійна різнорівнева робота. Учні, які виконали роботу швидко, можуть вирішити додаткове завдання, написане на дошці.

Варіант 1 Завдання «Лампа»

1.Вирішити квадратне рівняння

2.Менше значення кореня позначити х₁, більше значення кореня позначити х₂. У дужках після кожного рівняння вказано код: (х₁, х₂) або (х₂, х₁) – координати точок координатної площини. Відзначити на координатній площині точки і послідовно їх з'єднати, останню точку замкнути з першою.

1.х² - 9х + 18 = 0; (х₁, х₂)

2.2х² - 11х - 6 = 0; (х₂, х₁)

3.2х² - х - 1 = 0; (х₂, х₁)

4.х² + 6х - 7 = 0; (х₂, х₁)

5.х² + 6х - 27 = 0; (х₂, х₁)

6.х² + 12х + 27 = 0; (х₂, х₁)

7.x² + 8x + 7 = 0; (х₂, х₁)

8.2х² + 3х + 1 = 0; (х₁, х₂)

9.2х² + 13х + 6 = 0; (х₁, х₂)

10.х2 - 3х - 18 = 0; (х₁, х₂).

Варіант-2 Завдання «Глечик»

1.Вирішити квадратне рівняння

2.Менше значення кореня позначити х₁, більше значення кореня позначити х₂. У дужках після кожного рівняння вказано код: (х₁, х₂) або (х₂, х₁) – координати точок координатної площини. Відзначити на координатній площині точки і послідовно їх з'єднати, останню точку замкнути з першою.

1.х2 - 11 х + 18 = 0; (х₁, х₂)

2.2х2 - 9х + 10 = 0; (х₁, х₂)

3.2х2 - 11х + 5 = 0; (х₂, х₁)

4.х2 + 5х - 14 = 0; (х₂, х₁)

5.х2 + 9х +14 = 0; (х₂, х₁)

6.2х2 + 9х - 5 = 0; (х₁, х₂)

7.2х2 + 9х + 10 = 0; (х₁, х₂)

8.х2 - 7х - 18 = 0; (х₁, х₂)

9.2х2 - 22 х + 36 = 0; (х₁, х₂)

Варіант-3 Завдання Катер.

1.Вирішити квадратне рівняння.

2.Менше значення кореня позначити х₁, більше значення кореня позначити х₂. У дужках після кожного рівняння вказано код: (х₁, х₂) або (х₂, х₁) – координати точок координатної площини. Відзначити на координатній площині точки і послідовно їх з'єднати, останню точку замкнути з першою.

1.2х2 - 15х - 8 = 0; (х₂, х₁)

2.х2 – х – 12 = 0; (х₂, х₁)

3.х2 + 7х + 12 = 0; (х₁, х₂)

4.2х2 + 13х - 7 = 0; (х₁, х₂)

5.2х2 + 5х - 63 = 0; (х₁, х₂)

6.x2 + x - 2 = 0; (х₁, х₂)

7.2х2 + х - 1 = 0; (х₁, х₂)

8.4х2 - 32х - 17 = 0; (х₁, х₂)

9.4х2 - 30х - 16 = 0; (х₂, х₁).

Варіант-4 Завдання «Ваза»

1.Вирішити квадратне рівняння

2.Менше значення кореня позначити х₁, більше значення кореня позначити х₂. У дужках після кожного рівняння вказано код: (х₁, х₂) або (х₂, х₁) – координати точок координатної площини. Відзначити на координатній площині точки і послідовно їх з'єднати, останню точку замкнути з першою.

1.х2 - 10х + 21 = 0; (х₁, х₂)

2.х2 - 8х + 15 = 0; (х₁, х₂)

3.2х2 - 13х + 6 = 0; (х₂, х₁)

4.х2 + 3х - 28 = 0; (х₂, х₁)

5.х2 + 4х - 45 = 0; (х₂, х₁)

6.х2 + 14х + 45 = 0; (х₂, х₁)

7.x2 + 11x + 28 = 0; (х₂, х₁)

8.2х2 + 11х - 6 = 0; (х₁, х₂)

9.х2 - 2х - 15 = 0; (х₁, х₂)

10.х2 - 4х - 21 = 0; (х₁, х₂)

Додаткове завдання на дошці:

1 рівень.

2 рівень.

9.                 Домашнє завдання.