Конспект уроку з алгебри в 7 класі на тему: «Лінійна функція, її графік і властивості»

Новосільська загальноосвітня школа І-ІІІ ступенів
імені М. Зарицького

 

 

 

 

 

 

 

 

Конспект уроку з алгебри в 7 класі

на тему:

«Лінійна функція, її графік і властивості»

 

 

 

 

 

 

 

 

Вчитель математики
Смеречинський Б.В.

 

 

 

 

 

Тема уроку:  Лінійна функція, її графік і властивості.

 

Мета уроку: Ввести поняття лінійної функції, показати побудову її графіка, встановити деякі властивості лінійної функції; формувати вміння і навички розв’язування вправ.

 

Обладнання: Підручник «Алгебра 7 клас» (В. Кравчук, М. Підручна,
Г. Янченко), комп’ютер (Прогама «Геогебра»), мультимедійна дошка, проектор, документ-камера.

 

Хід уроку.

 

І. Організаційний момент.

 

ІІ. Перевірка домашнього завдання:

 

Вправа 690.

а) Вода витікає з басейну;

б) Спочатку було 800 м³ води, а через 4 год — 0 м³.

 

Вправа 692.

а) Через 2 с — 4 м/с; 5 с — 10 м/с; 10 с — 10 м/с; 20 с — 0 м/с;

б) 4 м/с — через 2 с і 16 с; 6 м/с — через 3 с і 14 с; 8 м/с — через 4 с і 12 с;

в) Найменшою була швидкість в 0 с і 20 с;

г) Зі сталою швидкістю тіло рухалося на протязі 5 с — від 5 с до 10 с і пройшло за цей час шлях S = Vt = 10·5 = 50 (м).

 

ІІІ. Актуалізація опорних знань учнів:

 

1. Що називається функцією?

2. Як називається множина незалежних змінних?

3. Як по іншому називають незалежну змінну?

4. Як називається множина залежних змінних?

5. Як по іншому називають залежну змінну?

6. Які способи задання функцій вам відомі?

 

ІV. Вивчення нового матеріалу:

 

1. Означення лінійної функції.

2. Область визначення лінійної функції.

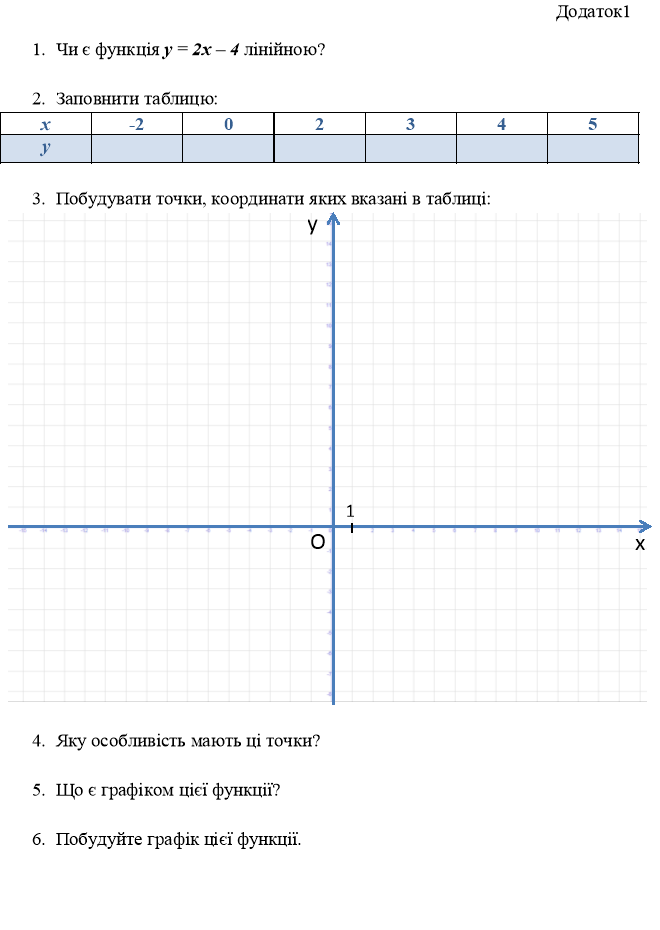
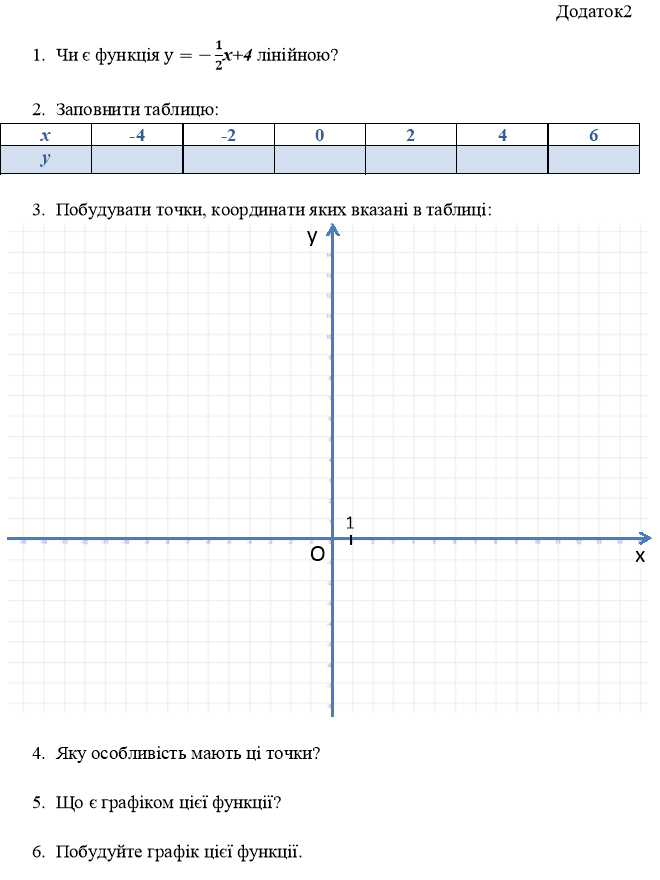
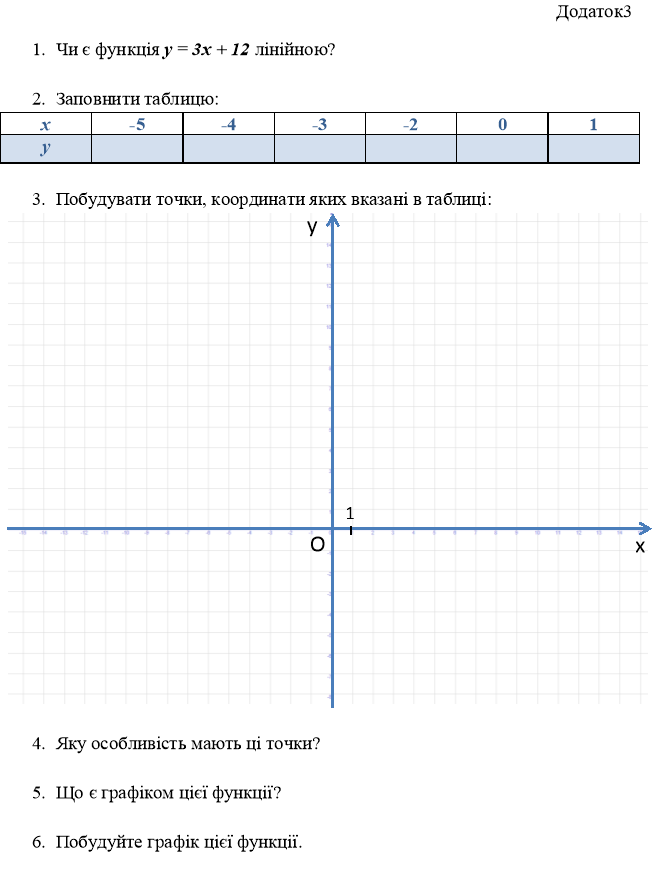
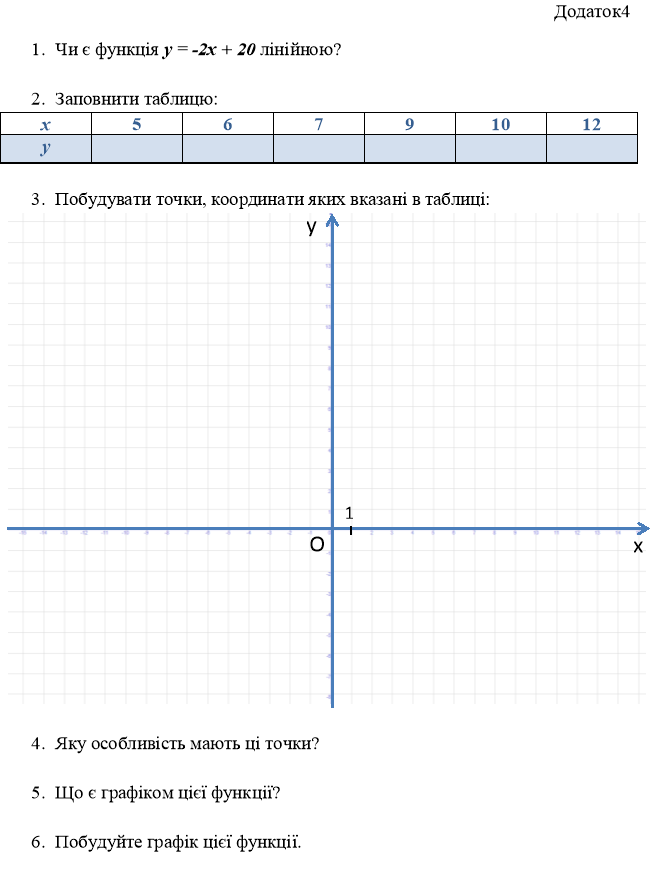
3. Робота груп з картками (додаток1, додаток2, додаток3, додаток4):

а) заповнення таблиці;

б) побудова в системі координат точок, координати яких записані в таблиці;

в) висновок про те, що ці точки лежать на одній прямій;

г) висновок про те, що графіком лінійної функції є пряма;

д) встановлення мінімальної кількості точок для побудови графіка лінійної функції.

Кожна група на своїй картці в системі координат побудувала вказані точки. З допомогою документ-камери, підключеної до комп’ютера, через проектор на дошці демонструється розташування точок в системі координат. При правильних розрахунках, на кожній картці видно, що точки лежать на одній прямій. Враховуючи те, що областю визначення лінійної функції є множина всіх дійсних чисел, точок на кожній картці може бути безліч, учні припускають, що всі вони утворюють суцільну пряму лінію. Оскільки так відбувається для всіх запропонованих лінійних функцій, робиться висновок, що графіком кожної з цих, та й інших лінійних функцій є пряма. З уроків геометрії учні знають, що для побудови прямої достатньо знати координати лише двох її точок. Тому дальше розробляється алгоритм побудови графіка лінійної функції, який передбачає обчислення координат двох точок, які належать прямій.

4. Побудова графіка функції у = 3х – 2 на дошці і в зошитах.

5. Кутовий коефіцієнт прямої.

Використовуючи комп’ютерну програму «Геогебра», на дошці через проектор виводиться графіки чотирьох заданих на картках лінійних функцій. Для кращого сприймання, дві з цих прямих, нахилених під гострим кутом до додатного напряму осі абсцис можна виділити іншим кольором. Дальше ставиться учням запитання про зв'язок між знаком числа, яке вони бачать перед х в записі функцій і кутом нахилу прямої до осі абсцис. Учні швидко роблять висновок, що кут нахилу прямої залежить від цього числа, тому його називають кутовим коефіцієнтом.

6. Особливі випадки лінійної функції (k = 0; b = 0):

а) функція у = b, її графік і область значень;

б) функція у = kx, її графік, кут нахилу прямої.

Для того, щоб учні зрозуміли, як виглядає графік функції у = b, засобами «Геогебра» будуємо кілька прикладів таких графіків. Учні швидко роблять висновок, що графіком має бути пряма, паралельна до осі абсцис, проведена через точку на осі у з ординатою b.

Для визначення особливостей побудови графіка прямої пропорційності, будуємо кілька прикладів таких графіків. Побачивши їх, учні роблять висновок, що графік прямої пропорційності повинен проходити через початок координат, а тому для його побудови достатньо знати координати лише ще однієї точки, яка йому належить.

7. Властивості лінійної функції:

а) область визначення функції утворюють усі числа;

б) якщо k ≠ 0, то область значень функції утворюють усі числа; якщо k = 0, то функція набуває лише одного значення у = b;

в) графіком функції є пряма;

г) графік функції утворює з додатним напрямом осі х гострий кут, якщо k > 0, тупий кут,— якщо k < 0. Якщо  k = 0, то графік паралельний осі х, зокрема, якщо k = 0 і b = 0, то він збігається з віссю х.

 

V. Закріплення вивченого матеріалу:

 

Вправи: 703, 704, 705, 712, 716.

 

VІ. Підсумки уроку.

 

VІІ. Завдання додому: п. 21, вправи 713, 717.

 

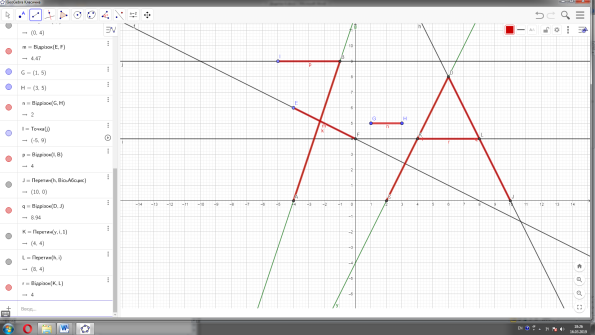
VIII. Розгадка ребуса.

На графіках, які використовувалися під час уроку утворити відрізки кінці яких мають координати:

АВ А (-4; 0), В (-1; 9),

CD C (2; 0), D (6; 8),

EF E (-4; 6), F (0; 4),

GH G (1; 5), H (3; 5),

IB I (-5; 9), В (-1; 9),

DJ D (6; 8), J (10; 0),

KL K (4; 4), L (8; 4).

Учні повинні спостерігати за побудовою відрізків (побудова відрізків ведеться іншим кольором) і розгадати зашифрований напис, можливо, ще до появи всіх відрізків на дошці.