Конспект уроку з математики для 4 класу за системою розвивального навчання "Обчислення площі правильного шестикутника"

 

Тема: Обчислення площі правильного шестикутника

Мета: вивести спосіб обчислення площі правильного шестикутника;

удосконалювати уміння визначати периметр і площу вивчених                     геометричних фігур;                                                                        

вправлятися у розв'язанні задач, пов'язаних з периметром та площею прямокутника, трикутника;

розвивати пізнавальний інтерес, дивергентність мислення, уміння відрізняти раціональний і нераціональний способи розв'язання;

виховувати зацікавленість процесом навчання, старанність, працелюбність.                            

Обладнання: демонстраційний матеріал: геометричні фігури, картки з

             формулами обчислення периметра вивчених геометричних фігур;

             роздатковий матеріал: правильні шестикутники, маркери, ножиці.

 

ЗМІСТ УРОКУ

 

І. Створення навчальної ситуації успіху

1. -  Над якими математичними величинами ми працювали на попередніх уроках? (Площею, периметром.)

           - Що таке периметр?

           - Площі яких фігур ми навчилися знаходити?

            - Що необхідно знати для знаходження площі і периметра фігури ?

          - А чи знаєте ви яка наука їх вивчає ?

Це наука - «геометрія». Вона виникла дуже давно і є однією  з найстародавніших наук. Батьківщиною геометрії вважають звичайно Вавилон і Єгипет.

Основоположниками  її  є Архімед, Евклід, Піфагор. І ми навіть не уявляємо наскільки часто можемо зустрітися з геометрією у нашому житті.

        -Геометрія навколо нас. Ось про що піде мова на нашому уроці. Адже, коли придивитися уважно, то нас оточує безліч геометричних фігур та тіл.

     - Вам додому було завдання: дослідити, які геометричні фігури і тіла нас оточують.(У транспорті найчастіше зустрічаються коло та циліндр.

У побуті - коло, циліндр, прямокутник, квадрат, паралелепіпед, круг, шар. Тварини використовують найчастіше півкулю, шар, шестикутник.)

_Отже, сьогодні на уроці ми з вами пізнавати таємниці геометричних фігур та закріпимо уміння знаходити площу та периметр вивчених фігур/

ІІ. Постановка навчальної задачі

1. -   На аркушах по класу розвішані геометричні фігури.

     - За якими ознаками їх можна об’єднати  у дві групи? ( 1 група – чотирикутники, 2 група – трикутники.)

• Яку назву має кожна фігура?
• (Прямокутник, паралелограм, рівнобедрена трапеція, ромб, квадрат, різносторонній трикутник, рівносторонній трикутник, рівнобедрений трикутник.

 

 

 

 

 

 

 

2. – За формулою знаходження периметра впізнайте відповідну фігуру:     

Р = (а + в) · 2  Р = 4а             Р = 2а + в         Р= 2а

Р = а + в + с · 2  Р = а + в + с   Р = 3а            Р = 6а

• Оберіть будь-яку фігуру, відповідні мірки і знайдіть її периметр.

3. - У яких фігур ми вміємо знаходити площу? (У прямокутника і будь-якого трикутника.)

Обчисліть площу прямокутника і трикутника, якщо:

              а=6,5 см                              h=4 см

              в=2 см                                 а=8,1 см

              S-?                                       S-?

6,5 ∙ 2= 13  4 ∙ 8,1: 2=32,4 :2 = 16,2

 

(Робота по варіантах. Два учні виконують біля дошки)

• Дякую за роботу. Ви успішно виконали завдання на знаходження периметра і площі фігури. Показали розуміння формул та знання особливостей геометричних фігур.

Фізкультхвилинка

-Я називаю фігуру, а ви відповідно виконуєте стільки стрибків чи поворотів навколо себе, скільки кутів має ця фігура. Якщо фігура не має кутів, то сідаєте за парту.

III. Розв’язання навчальних задач уроку

- Сьогодні на уроці ми більше дізнаємося про одну геометричну фігуру. Вона об’єднує  такі поняття: олівець, гайка, сніжинка, бджолині соти. Що це за фігура?( Правильний шестикутник)

-Який шестикутник називають правильним?( Той у якого всі сторони і кути рівні)

- А як ви гадаєте, чому саме його з поміж інших фігур обрали для своїх сот бджоли?

( На дошці геометричні фігури - трикутник, квадрат, шестикутник)

- Серед правильних трикутника, квадрата та шестикутника, найбільшу площу має саме шестикутник. І це допомагає бджолам найбільш економно використовують площу всередині невеликого вулика та  використовуючи при цьому найменшу кількість воску. І як говорила бджола із казки «Тисяча і одна ніч»: «Мій будинок збудований за законами самої точної архітектури. Сам Евклід міг би повчитися, пізнаючи геометрію моїх сот».

 Бджоли тісно пов’язані з квітами.

- Чи любите ви квіти?

- Які квіти вам найбільше подобаються?

- Яку роль відіграють квіти у житті людини?

- Де вирощують квіти?

 - До нас прийшла різнобарвна весна. Прикрасила рідну землю. І учні однієї школи вирішили допомогти їй: на шкільному подвір’ї розбити клумбу у формі ось такого правильного шестикутника.

- А для того, щоб їхня клумба була красивою, незвичайною, вони вирішили замовити в одному квітковому господарстві троянди. Там працюють чудові працьовиті люди, які дарують людям радість: вирощують квіти.     А хто з вас знає, як називають людей цієї професії? (Квітникарі).   Але щоб визначити кількість кущів потрібно дізнатись площу квітника шестикутної форми. Вони звернулись до нас за допомогою. Спробуємо їм допомогти?

ІV. Розв’язання навчальної задачі.

1.   Для цього пригадаємо:  як знайти площу любого многокутника? (Для цього потрібно розбити цей многокутник на фігури, площі яких ми уміємо знаходити. )
2.   Практична робота: розбиваємо шестикутник на фігури, площі яких ми уміємо знаходити. Робота в групах
3.   Діти, ви створили декілька проектів. Захистіть їх: поясніть площі яких фігур потрібно знайти для того, щоб обчислити площу шестикутника. (захист проектів)
4.   Діти іншого класу теж обмірковували цю проблему. Вони також розбивали 6-кутники і придумали кілька способів: ( На дошці)

 

 

 

 

 

 

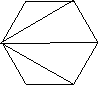
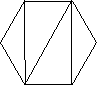
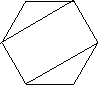
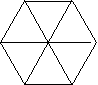
- Який спосіб для обчислення площі 6-тикутника буде найкращий? Як ви про це дізнаєтесь?

- Вивчення трикутників породило цілу науку тригонометрію. Слово тригонометрія походить від грецьких слів «тригон» що означає трикутник і

«метрео» – вимірюю.

5.Практична робота: визначення площі і периметра правильного 6-тикутника.

• Які вимірювання необхідно виконати для того, щоб обчислити площу трикутника? (Потрібно виміряти його основу й висоту.)
• Якою формулою будемо користуватись? (S=a∙h:2) а= 10,5 см, h = 9 см

10,5 ∙ 9= 94,5 : 2= 47,25

•  
• Площу трикутника знайдіть самостійно.
• Порівняйте свої результати.
• А тепер знайдіть площу правильного шестикутника. S=(a∙h:2)∙ 6

47,25 ∙ 6 =283,5

• Для обгородження клумби потрібно замовити бардюрний камінь для цього потрібно знати її периметр. Як знайти периметр правильного шестикутника? (P=a∙6)    10,5 ∙ 6= 63
• Самостійно виконайте обчислення.
• Підведемо підсумки. Як потрібно знаходити площу і периметр правильного шестикутника?
• Діти, ми з вами добре попрацювали і я думаю, що нам будуть вдячні за таку допомогу.

V. Підсумкова рефлексія.

• Над якими завданнями ми працювали на сьогоднішньому уроці?
• Що нового дізнались?
• Кому б ви хотіли подякувати і за що?
• Оцініть свою діяльність на уроці та діяльність класу.
• Оцінки за урок ви отримаєте після перевірки самостійної роботи в зошиті.