Конспект уроку з математики для 5 класу на тему "Дроби і ділення"
Математика
Тема уроку: Дроби і ділення
Мета уроку:
- навчальна: удосконалити вміння розв’язувати задачі на застосування зв’язку між дією ділення і звичайними дробами; сформувати поняття мішаного числа, його цілої і дробової частин; сформувати вміння виділити цілу частину з неправильного дробу;
- розвивальна: формувати вміння грамотно формулювати власні думки; сприяти розвитку логічного мислення, уваги учнів;
- виховна: виховувати інтерес до вивчення математики, почуття відповідальності, дисциплінованість.
Тип уроку: удосконалення знань, умінь, навичок.
Обладнання та наочність: підручник, наочний роздатковий матеріали.
Форма роботи: діалог, інтерактивне спілкування, практичне застосування набутих знань.
Дата проведення: 5-Б – 22.01.2015
Хід уроку
І. ОРГАНІЗАЦІЙНИЙ ЕТАП
- Привітання вчителя і учнів.
- Організація готовності учнів до уроку, налаштування їх на роботу.
ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ
- Перевірка завдання, заданого за підручником
№ 921. Запишіть у вигляді дробу:
- 3 : 7; 2) 15 : 5; 3) 21 : 5; 4) 1 : 4.
З отриманих дробів випишіть:
- правильні дроби; б) неправильні дроби.
Розв’язання:
-
3 : 7 =
 ; 2) 15 : 5 =
; 2) 15 : 5 = 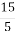 ; 3) 21 : 5 =
; 3) 21 : 5 = 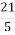 ; 4) 1 : 4 =
; 4) 1 : 4 =  .
.
а) ![]() – правильні дроби; б)
– правильні дроби; б) ![]() – неправильні дроби.
– неправильні дроби.
№ 926. Запишіть 1 у вигляді дробу з чисельником:
- 7; 2) 111; 3) 56; 4) 13; 5) 2369; 6)100.
Розв’язання:
-
1 =
 ; 2) 1 =
; 2) 1 = 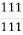 ; 3) 1 =
; 3) 1 = 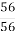 ; 4) 1 =
; 4) 1 = 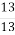 ; 5) 1 =
; 5) 1 =  ; 6) 1 =
; 6) 1 = 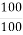 .
.
№ 928. Запишіть число 5 у вигляді дробу з знаменником:
- 5; 2) 10; 3) 50; 4) 25; 5) 40; 6) 100.
Розв’язання:
-
5 =
 ; 2) 5 =
; 2) 5 = 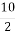 ; 3) 5 =
; 3) 5 = 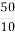 ; 4) 5 =
; 4) 5 = 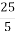 ; 5) 5 =
; 5) 5 = 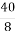 ; 6) 5 =
; 6) 5 = 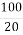 .
.
№ 932. Порівняйте:
-
8 : 3 і
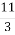 ; 2) 25 : 12 і
; 2) 25 : 12 і 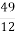 ; 3) 125 : 15 і
; 3) 125 : 15 і 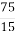 ; 4) 124 : 17 і
; 4) 124 : 17 і 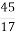 .
.
Розв’язання:
-
8 : 3
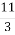 ; 2) 25 : 12
; 2) 25 : 12 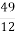 ; 3) 125 : 15
; 3) 125 : 15 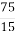 ; 4) 124 : 17
; 4) 124 : 17 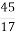 ;
;
![]()
![]() .
. ![]()
![]() .
. ![]()
![]() .
. ![]()
![]() .
.
- Відповісти на питання, що виникли у учнів під час виконання домашніх вправ.
- Математичний диктант
- Запишіть дробом ділення чисел 24 на 6, 28 на 7.
-
Ділення яких чисел означають дроби
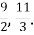
- Запишіть частку 17:9 і 19:4 у вигляді дробу.
-
Якому натуральному числу дорівнює дріб
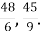
- Запишіть числа 14 і 13 у вигляді дробу зі знаменником 2.
ІІІ. ОГОЛОШЕННЯ ТЕМИ І МЕТИ УРОКУ
- Сьогодні ми продовжуємо вивчати тему: «Дроби і ділення».
- Метою сьогоднішнього уроку є: якомога найкраще засвоїти правила виділення цілої частини з неправильного дробу та перетворення мішаного числа у неправильний дріб, а також закріпимо ваші вміння під час розв’язування завдань, що передбачують перетворення неправильного дробу у мішане число і навпаки.
ІV. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
V. УДОСКОНАЛЕННЯ ЗНАНЬ
План вивчення теми
- Означення мішаного числа.
- Означення цілої і дробової частини числа.
- Правило виділення цілої частини з неправильного дробу.
- Приклади запису неправильного дробу у вигляді мішаного або натурального числа:
Пояснення вчителя
Ви знаєте, що одне натуральне число можна поділити націло, або з остачею. Наприклад, 30 : 6 = 5, а 30 : 7 = 4 (остача 2). Якщо частку подати у вигляді дробу, то ці рівності можна записати так: ![]() = 5 і
= 5 і ![]() = 4 +
= 4 + ![]() .
.
З першого прикладу слідує, що будь-яке натуральне число можна подати у вигляді дробу: 5 = ![]() .
.
Суму 4 + ![]() коротко записується 4
коротко записується 4![]() і читають «чотири цілі дві сьомі».
і читають «чотири цілі дві сьомі».
Число 4![]() – це число нового виду. Його називають мішаним числом. У його запису натуральне число 4 називається цілою частиною, а дріб
– це число нового виду. Його називають мішаним числом. У його запису натуральне число 4 називається цілою частиною, а дріб ![]() – дробовою частиною.
– дробовою частиною.
Зверніть увагу: мішане число дорівнює сумі його цілої і дробової частин; дробова частина мішаного числа завжди є правильним дробом.
Дія за допомогою якої неправильний дріб перетворюють у мішане число (або натуральне число), називається виділенням цілої частини з неправильного дробу.
Правило виділення цілої частини з неправильного дробу.
Щоб виділити цілу частину з неправильного дробу, треба:
- чисельник даного дробу поділити на знаменник;
- частку записати, як цілу частину шуканого мішаного числа;
- у знаменник дробової частини записати знаменник даного дробу;
- у чисельник дробової частини записати остачу від ділення.
Наприклад, ![]() .
.
Правило перетворення мішаного числа у неправильний дріб.
Щоб перетворити мішане число у неправильний дріб, треба:
- у знаменник шуканого дробу записати знаменник дробової частини;
- цілу частину помножити на знаменник дробової частини;
- до отриманого добутку додати чисельник дробової частини;
- отриману суму записати в чисельник шуканого дробу.
Наприклад, ![]() .
.
V. УДОСКОНАЛЕННЯ ВМІНЬ І НАВИЧОК
1. Робота за підручником (§ 24) Ст. 206.
Усно: № 918, № 919.
№ 918. Прочитайте числа:
-
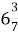 ; 2) 4
; 2) 4 ; 3) 12
; 3) 12 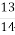 ; 4) 7
; 4) 7 .
.
Назвіть: а) цілу частину мішаного числа; б) дробову частину мішаного числа.
Відповідь:
а) 6, 4, 12, 7; б)![]() ;
;![]() ;
; ![]() ;
;![]() .
.
№ 919. Чи може дробова частина мішаного числа дорівнювати:
-
 ; 2)
; 2)  ; 3)
; 3) 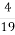 ; 4)
; 4) 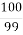 .
.
Відповідь:
- так; 2) ні; 3) так; 4) ні.
Письмово: № 922, 933, 943, 945, 947.
№ 922. Запишіть у вигляді мішаного числа:
-
5+
 ; 2) 7+
; 2) 7+  ; 3) 12+
; 3) 12+ 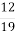 ; 4) 111+
; 4) 111+ 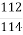 .
.
Розв’язання:
-
5+
 =
= 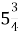 ; 2) 7+
; 2) 7+  =
= 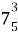 ; 3) 12+
; 3) 12+ 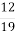 =
= 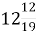 ; 4) 111+
; 4) 111+ 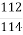 =
= 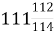 .
.
№ 933. Виділіть цілу частину з неправильного дробу:
-
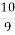 ; 2)
; 2) 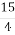 ; 3)
; 3) 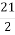 ; 4)
; 4) 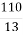 ; 5)
; 5) 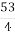 ; 6)
; 6) 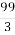 .
.
Розв’язання:
-
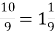 ; 2)
; 2)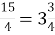 ; 3)
; 3) 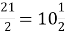 ;
;
4) ![]() ; 5)
; 5)![]() ; 6)
; 6)![]() .
.
№ 943. Виділіть цілу частину з неправильних дробів: ![]() Запишіть отримані числа в порядку зростання. Який із цих дробів найбільший?
Запишіть отримані числа в порядку зростання. Який із цих дробів найбільший?
Розв’язання:
![]()
1, 3, 5, 9.
Найбільший дріб – ![]() .
.
№ 945. Накресліть координатний промінь і позначте на ньому точки, що відповідають числам:
-
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  . Яке з чисел розміщується найближче до початку координат?
. Яке з чисел розміщується найближче до початку координат?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Відповідь: х
Відповідь: х
0 ![]()
![]()
![]()
![]()
![]() – розміщається найближче до початку координат.
– розміщається найближче до початку координат.
№ 947. Порівняйте:
-
3
 і
і 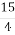 ; 2) 7
; 2) 7 і
і 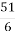 ; 3) 15
; 3) 15 і
і 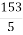 ; 4) 124
; 4) 124 і
і 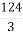 .
.
Розв’язання:
-
3

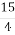 ; 3) 15
; 3) 15
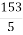 ;
;
![]()
-
7

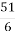 ; 4) 124
; 4) 124
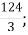
![]()
VI. ПІДСУМКИ УРОКУ
- Підсумкова бесіда
Отже, давайте повторимо основні правила, які ми вивчили сьогодні на уроці:
- Як перетворити мішане число у неправильний дріб?
- Що таке мішане число? Наведіть приклад.
- Яким дробом є дробова частина мішаного числа?
- Як перетворити неправильний дріб у мішане число?
- Оцінювання учнів. Мотивація оцінок
VII. ДОМАШНЄ ЗАВДАННЯ
- Завдання за підручником: Н.А. Тарасенкова, І.М. Богатирьова, О.П. Бочко, О.М. Коломієць, З.О. Сердюк. Розділ V, § 24, № 923, 934, 944, 948.
- Інструктаж:
- № 923 подібний до № 922, що ми щойно виконували на уроці.
- № 934 подібний до № 933.
- № 944. Подібний до № 943. Щоб виконати ці номери вам потрібно знати правило виділення цілої частини з неправильного дробу.
- № 948 подібний до № 947. Щоб виконати цю вправу без проблем, вам необхідно повторити правило перетворення мішаного числа у неправильний дріб.
- І обов’язково почитайте § 24, і вивчіть всі основні правила. Підготуйтеся до Самостійної роботи.
1


про публікацію авторської розробки
Додати розробку
