Конспект уроку з математики для 5 класу на тему "Знаходження числа за його дробом"

Математика

Тема уроку: Знаходження числа за його дробом

Мета уроку:

• навчальна: домогтися засвоєння правила знаходження числа за його дробом; сформувати вміння виконувати вправи, у яких передбачено знаходження числа за його дробом; узагальнити і систематизувати знання учнів з теми «Звичайні дроби»;
• розвивальна: сприяти розвитку творчих здібностей, логічного мислення учнів;
• виховна: виховувати наполегливість, старанність,;

Тип уроку: засвоєння нових знань, умінь, навичок.

Обладнання та наочність: підручник, наочний та роздатковий матеріали.

Форма роботи: діалог, інтерактивне спілкування, практичне застосування набутих знань.

Дата проведення:   5-Б – 28.01.2015                                

Хід уроку

І. ОРГАНІЗАЦІЙНИЙ ЕТАП

1. Привітання вчителя і учнів.
2. Організація готовності учнів до уроку, налаштування їх на роботу.

ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

1. Перевірка завдання, заданного за підручником

№ 970.Знайдіть:

1. від 9;                          2) від 12;                        3) від 20;      

4) від 32;                         5) від 80;                       6) від 49.

Розв’язання:

1. 9 : 3  2 = 6;                2) 12 : 4  3 = 9;                    3) 20 : 5  4 = 16;

4) 32 : 4  7 = 56;             5) 80 : 20  21 = 84;              6) 49 : 7  12 = 84.

№ 971. Накресліть відрізок АВ завдовжки 6 см та відрізок CD, довжина якого становить:

1. довжини відрізка АВ;                       3) довжини відрізка АВ;
2. довжини відрізка АВ;                       4) довжини відрізка АВ.

Розв’язання:

1. від 6, це – 6 : 3  1 = 2,  CD = 2 см;   3)від 6, це –6 : 2  3 = 9, CD = 9 см;
2. від 6, це – 6 : 3  2 = 4,  CD = 4 см;   4) від 6, це – 6 : 6  7 = 7, CD = 7 см.

А         6 см В

1. C  2 см   D                               3)   C                       9 см                         D

2. C  4 см             D                      4)    C                   7 см               D

2. Відповісти на питання, що виникли у учнів під час виконання домашніх вправ.
3. Математичний диктант

1. Щоб знайти дріб від числа, треба дане число поділити на знаменникдробу і одержаний результат помножити на йогочисельник.
2. Якими способами можна розв'язувати задачі на знаходження дробу від числа? Арифметичним і алгебраїчним.
3. Які задачі називають задачами на знаходження дробу від числа? Задачі під час розв'язування яких доводиться знаходити число, яке від данного числа становить, наприклад .

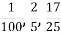ІІІ. ПОВІДОМЛЕННЯ ТЕМИ ТА МЕТИ УРОКУ

• Сьогодні ми розглянемо тему: «Знаходження числа за його дробом».
• Метою сьогоднішнього уроку є: якомога найкраще засвоїти правило знаходження числа за його дробом; також навчимося розв’язувати задачі, які передбачають знаходження числа за його дробом.

ІV. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

V. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

План вивчення теми

1. Як знайти число за його дробом?
2. Способи знаходження числа за його дробом:

1. арифметичний;
2. геометричний.

3. Приклади знаходження числа за його дробом.

Пояснення вчителя

На практиці часто доводиться розв’язувати обернену задачу. Тобто знаходити число, знаючи, щодеяке число становить його частину. Такі задачі називають задачами на знаходження числа за його дробом.

                              Способи розв’язування задач

Задача. Площа території Норвегії – 384 000 км², що становить площі території України. Яка площа території України?

Розв'язування.

1. Арифметичний спосіб.

1. Скільки км² становить 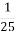площі території Норвегії?

 384 000 : 16 = 24 000 (км²).

2. Скільки км² становить 25 таких частин?

24 000 · 25 = 600 000 (км²).

Отже, площа території України становить 600 000 км².

2. Алгебраїчний спосіб.

Норвегія – 384 000 км² -

Україна – ? –

Нехай х – площа території України. Тоді:

           х : 25 = 384 000 : 16,

           х = (384 000 : 16) · 25,

           х = 24 000 ·25,

           х = 600 000.

Відповідь:  площа території України становить 600 000 км².

Правило знаходження числа за його дробом

Щоб знайти число за його дробом, треба дане число поділити на чисельник дробу і одержаний результат помножити на його знаменник.

Зверніть увагу:

1. число, яке приймаєте за 1, виразіть неправильним дробом із тим самим знаменником, що й заданий дріб;
2. щоб скласти рівняння, складіть вирази для однієї частини від заданного числа і від шуканого числа та прирівняйте їх.

VІ. ЗАСВОЄННЯ НОВИХ ЗНАНЬ І ВМІНЬ

1. Робота за підручником (§ 25)

Усно: № 968, 969.

№ 968.Укажіть правильне закінчення правила.

Щоб знайти число за його дробом, треба дане число … :

1. помножити на чисельник дробу і поділити на йогознаменник;
2. поділити на чисельник дробу і помножити на його знаменник.

№ 969.У якому з двох випадків Андрійко міркував правильно?

Щоб знайти число, якого дорівнює 48, треба:

1. 48 : 8 = 6, а потім 6  12 = 72;
2. 48 : 12 = 4, а потім 4 · 8 = 32.

Письмово: № 980, 981, 982.

№ 980.Знайдіть число, якщо:

1. його дорівнює 12;                                   2)  його дорівнюють 30;

3. його 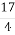дорівнюють 68;                            4)  його дорівнюють 28;

5. його дорівнюють 45;                              6)  його 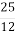дорівнюють 150.

Розв’язання:

1. (12 : 1) · 3 = 12 · 3 = 36;                                2) (30 : 5) · 6 = 6 · 6 = 36;

3. (68 : 17) ·4 = 4 · 4 = 16;                                 4) (28 : 2) · 7 = 14 · 7 = 28;

5. (45 : 9) ·5 = 5 · 5 = 25;                                   6) (150 : 25) · 12 = 6 · 12 = 72.

№ 981.Чому дорівнює довжина відрізка АВ, якщо:

1. його довжини дорівнює 5 см;
2. його довжини дорівнюють 15 см;
3.   його довжини дорівнюють 24 см?

Розв’язання:

1. АВ = (5 : 1) · 2 = 5 · 2 =10 см;
2. АВ = (15 : 5) ·7 = 3 · 7 = 21 см;
3. АВ = (24 : 4) · 3 = 6 · 3 = 18 см.

№ 982.Чому дорівнює кут, якщо:

1. його дорівнюють прямому куту;
2. його дорівнюють прямому куту:
3. його дорівнюють розгорнутому куту?

Розв’язання:

1. = (90 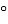: 2) · 3 = 45 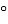· 3 = 135;
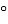2.  = (90 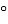: 5) · 9 = 18 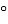· 9 = 162;
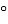3.  = (180 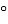: 9) · 2 = 20 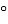· 2 = 40.

VІ.ПІДСУМКИ УРОКУ

1. Підсумкова бесіда

Отже, давайте з вами ще раз повторимо вивчені сьогодні правила:

• Як знайти число за його дробом?
• Які є способи розв’язування задач на знаходження числа за його дробом?

2. Оцінювання учнів. Мотивація оцінок

VІІ. ДОМАШНЄ ЗАВДАННЯ

1. Завдання за підручником: Н.А. Тарасенкова, І.М. Богатирьова,           О.П. Бочко, О.М. Коломієць, З.О. Сердюк. Розділ V, § 25, № 983.
2. Інструктаж:

1. № 983 подібний до № 982, що ми виконували сьогодні з вами на уроці. Щоб при виконанні цього номера у вас не виникло проблем, вам потрібно повторити скільки градусів дорівнює прямий і розгорнутий кути, а також знати правило знаходження числа за його дробом.
2. І обов’язково почитайте § 25 та вивчіть основні правила.