Конспект уроку з математики у 6 класі на тему: "Дії з раціональними числами""
Математика 6 клас
Тема. Дії з раціональними числами.
Мета: закріпити вміння і навички розв’язування вправ з теми „Дії з раціональними числами”; розвивати логічне мислення та творчі здібності учнів; виховувати почуття патріотизму та потребу вивчати історію рідного краю.
Тип уроку: урок узагальнення і систематизації знань.
Форма проведення уроку: урок-екскурсія.
Методи та прийоми: самостійна робота, робота в парах, робота вгрупах, гра „Загублені знаки”.
Обладнання: картки з тестовими завданнями, картки для групової роботи, фотографії Почаївської лаври.
Хід уроку
- Повідомлення теми та мети уроку
Вчитель.Сьогодні в нас особливий урок-екскурсія на тему „Дії з раціональними числами”. Ми не тільки повторимо і узагальнимо навички виконання дій додавання, віднімання, множення і ділення раціональних чисел, але й дізнаємося багато цікавих фактів про культурну й духовну перлину кременеччини — Почаївську Лавру.
- Мотивація навчальної діяльності учнів
Вчитель. Що ви знаєте про Почаївську лавру?
Кожен з вас — маленький українець. Тому дуже важливо не тільки вміло оперувати математичними термінами і розв’язувати приклади та задачі, а й знати історію своєї рідної землі. Тож сьогодні всі завдання будуть стосуватися відомостей про Почаївську лавру.
- Повторення та систематизація теоретичних знань
Вчитель. Почаївська Лавра — це найбільша православна святиня Волині й друга після Києво-Печерської Лаври, в Україні. Історія свідчить, що ще в IX столітті на горі Почаївській несли подвиг ченці-пустинники — учні і послідовники святителя Мефодія, просвітителя слов’ян. А щоб дізнатися дату виникнення монастиря, вам потрібно виконати тестові завдання.
Виберіть букву, яка відповідає правильній відповіді.
I варіант
- Сумою двох чисел з різними знаками є число, що має такий самий знак, як і доданок з більшим модулем, а модуль суми дорівнює ... модулів доданків.
Б) добутку;
М) сумі;
В) різниці;
І) частці.
- Щоб від раціонального числа відняти інше, треба
О) від зменшуваного відняти модуль від’ємника;
Р) до зменшуваного додати модуль від’ємника;
Т) до зменшуваного додати число, протилежне від’ємнику;
К) від зменшуваного відняти число, протилежне від’ємнику.
- Добутком двох чисел з різними знаками є число ..., модуль добутку дорівнює добутку модулів множників.
С) нуль;
М) від’ємне;
Т) додатне.
- Часткою двох від’ємних чисел є число ...
А) від’ємне. Щоб знайти модуль частки, потрібно модуль діленого поділити на число, обернене до дільника.
В) від’ємне. Щоб знайти модуль частки, потрібно модуль діленого поділити на модуль дільника.
І) додатне. Щоб знайти модуль частки, потрібно модуль діленого поділити на число, обернене до дільника.
С) додатне. Щоб знайти модуль частки, потрібно модуль діленого поділити на модуль дільника.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
В |
Т |
Б |
М |
О |
А |
Р |
К |
І |
С |
II варіант
- Сумою двох відємних чисел є число ..., модуль якого дорівнює сумі модулів доданків.
Я) додатне;
Ф) нуль;
П) від’ємне.
- Добутком двох від’ємних чисел є число додатне. Модуль добутку доріввнює ...
Н) добутку чисел, обернених до множників;
З) добутку модулів множників;
Й) частці модулів множників;
Ж) частці чисел, обернених до множників.
- Щоб звести подібні доданки, потрібно ... їх коефіцієнти і результат помножити на спільну буквену частину.
У) помножити;
Д) відняти;
Л) поділити;
Н) додати.
- Часткою двох чисел з різними знаками є число .... Щоб знайти модуль частки, потрібно модуль діленого поділити на модуль дільника.
З) нуль;
Й) додатне;
Ж) від’ємне.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
П |
З |
Д |
Н |
Й |
Л |
У |
Я |
Ф |
Ж |
Вчитель. Правильно. Це 1240 рік. Спершу монастирськими келіями слугували ченцям печери в товщі гір, а першою будівлею була невеличка дерев’яна церква Успіння, яку звели в XIII столітті. Духовна історія Почаївської Лаври почалася з чуда.
Одного разу вночі почаївські іноки разом з пастухами побачили на вершині гори Богородицю, яка стояла на скелі у вогняному стовпі. З’явившись людям, зі сліпучою ясністю вона піднялася від землі на небо. Лише мить простояла Божа Матір на твердому камені, а слід її залишився назавжди. Свята стопа відбилася як на свічковому воску. З тих пір слід стопи на камені став наповнюватися водою, і вода ця — свята.
- Повторення і узагальнення практичних вмінь
![]()
![]() 1. Вчитель. І ось з’явилася людина, якій було не байдуже духовне становлення Почаєва. Щоб дізнатися її ім’я, потрібно, працюючи в парі, розв’язати приклади і розташувати їх результати в порядку зростання. Із відповідних букв утвориться її ім’я та прізвище. (Робота в парах).
1. Вчитель. І ось з’явилася людина, якій було не байдуже духовне становлення Почаєва. Щоб дізнатися її ім’я, потрібно, працюючи в парі, розв’язати приклади і розташувати їх результати в порядку зростання. Із відповідних букв утвориться її ім’я та прізвище. (Робота в парах).
![]()
![]() – 6,6 +1,5 = -5,1;
– 6,6 +1,5 = -5,1;
– 7,1 ∙ (- 3) = 21,3;
![]()
![]()
![]() ;
;
![]()
![]() – 1,5 + (- 4) = - 5,5;
– 1,5 + (- 4) = - 5,5;
![]()
![]()
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() 0 – ( -3,05) = 3, 05;
0 – ( -3,05) = 3, 05;
![]()
![]() - 8,2 + ( - 0,9) = - 9,1;
- 8,2 + ( - 0,9) = - 9,1;
![]()
![]() – 0,3 ∙0,5 = - 0,15;
– 0,3 ∙0,5 = - 0,15;
![]()
![]() – 6,5 – 9,4 = -15,9;
– 6,5 – 9,4 = -15,9;
![]()
![]()
![]() ;
;
![]()
![]()
![]() .
.
|
Число |
|
|
|
|
|
|
|
|
|
|
|
|
|
Буква |
Г |
а |
н |
н |
а |
Г |
о |
й |
с |
ь |
к |
а |
2. Вчитель. Будівництво справжнього монастиря почалося в XVI столітті, коли власниця цих земель Ганна Гойська, записала в земські книги свої великі пожертвування на будівництво Почаївської церкви. Крім цього, поміщиця подарувала монахам чудотворну ікону Почаївської Божої Матері, яка до наших днів знаходиться в Лаврі та зцілює вірян.
Історія святині також пов’язана з ігуменом, ім’я якого ви дізнаєтеся, розгадавши кросворд.
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
||
- Модуль кореня рівняння (3,5х + 6,1) – 21,4 = - 78,3.
- Значення виразу:
-10(7a - b) + 5(3b + 4a), якщо а = -7; b = - 10.
- Відстань між точками А(-17) і В(3) на координатній прямій.
(Ці завдання учні розв’язують колективно на дошці).
- (3,5х + 6,1) – 21,4 = - 78,3;
3,5х + 6,1 = - 78,3 + 21,4;
3,5х + 6,1 = - 56,9;
3,5х = - 56,9 - 6,1;
3,5х = - 63;
х = - 63 : 3,5;
х = - 18;
|x| =18.
Відповідь. 18.
- Якщо а = -7; b = - 10, то -10(7a - b) + 5(3b + 4a) = - 70а + 10b + 15b + 20a = -50a + 25b = - 50∙(- 7) + 25∙(-10) = 350 - 250 =100/
Відповідь. 100.
- |AB| = 3 – (-17) = 3 +17 = 20.
Відповідь. 20.
3. Вчитель. Преподобний Іов (Залізо) — 1551-1651 рр., уродженець Галицької Русі, прожив рівно сто років. Майже вісім років пролежало преподобного вземлі. І весь цей час люди бачили незвичайне світло над його могилою. В 1659 році мощі святого Іова були виявлені нетлінними. З того часу до сьогодні вони благоговійно перебувають в Лаврі. Святі мощі спочивають у Печерній церкві, яка осв![]() ячена в пам’ять преподобного Іова.
ячена в пам’ять преподобного Іова.
4. Але Почаївська Лавра — це не тільки духовна святиня, але й історико-архітектурний пам’ятник. Виконавши наступне завдання, ви дізнаєтеся, скільки церков входить до архітектурного комплексу лаври.
Гра „Загублені знаки”
Потрібно замістьзірочок поставити знак „+” або „-” , щоб рівність була правильною, і знайти суму номерів тих виразів, де поставили знак „+”. (Учні працюють усно).
- (* 3) ∙ (-0,7) = 2,1;
-
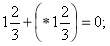
- – 6 +(*2) = - 4;
- (* 18) - (+4) = -22;
-
(* 6) :
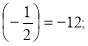
- (* 3) ∙ | -2,5| = -7,5;
-

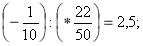
- – 3 +(* 5) = -8.
Відповідь. 3 + 5 + 8 = 16.
5. Вчитель. Головна споруда ансамблю — Успенський собор ренесансового стилю, збудований у 1771-1782 роках за проектом архітектора Готфріда Гофмана.
Для виконання наступного завдання об’єднайтеся у три групи.
Гра „Квіткова математика”
Кожній групі потрібно виконати дії. Кінцевий результат першої групи — висота Успенського собору, другої — довжина, а третьої — ширина.
Завдання для першої групи
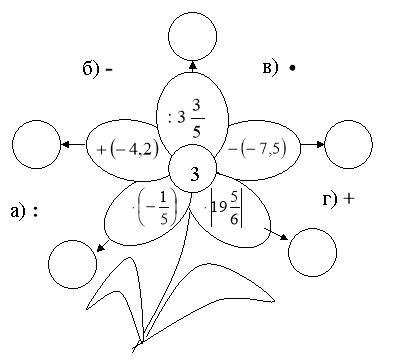
Відповідь. 56
![]()
![]() Завдання для другої групи
Завдання для другої групи
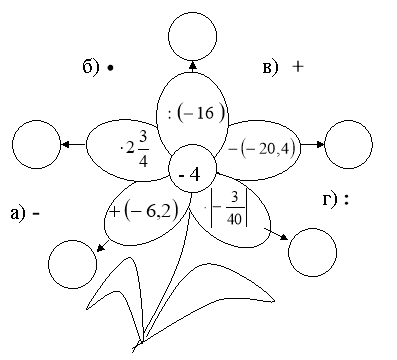
Відповідь. 54
Завдання для третьої групи
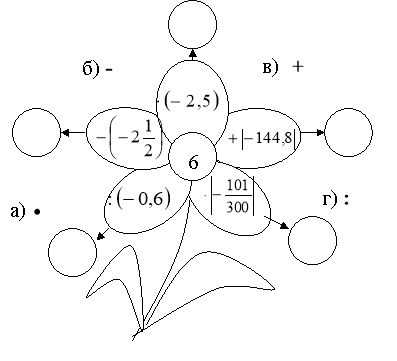
Відповідь. 40
Вчитель. Отже, 56 м — висота, 54 м — довжина і 40 м —ширина цієї величної споруди. Успенський собор вражає багатством золота й лазурі, живопису, ліній, граней, ярусів, геомутричних форм.
У давньоруському стилі новгородської архітектури XII – XIII століть споруджений протягом 1906-1912 років за проектом російського архітектора О.В. Щусєва Троїцький собор.
6. В архітектурну композицію лаври гармонійно вписується висока дзвіниця. А щоб дізнатися масу головного дзвона-велета, самостійно розв’яжіть рівняння. (Один учень працює на відкидній дошці).
3,5 – х = -8;
х = 3,5 – (-8);
х = 3,5 +8;
х = 11,5.
Відповідь.11,5
Вчитель. Правильно, цей дзвін важить приблизно 11,5 тонн.
7. Почаївську лавру відвідало багато видатних людей. А тепер обчисліть значення виразу:
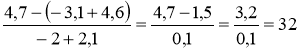
Відповідь.32
Вчитель. Це число виражає вік Т.Г.Шевченка, який у жовтні 1846 року у складі Київської археографічної комісії зробив чотири акварельні рисунки лаври.
Взагалі Почаїв відвідали у різний час Микола Костомаров, Михайло Драгоманов, Максим Рильський, Микола Бажан, Олесь Гончар, Дмитро Павличко, Ліна Костенко та інші.
- Підсумок уроку
Оцінювання учнів.
- Повідомлення домашнього завдання
Повторити матеріал з теми „Дії з раціональними числами”.


про публікацію авторської розробки
Додати розробку
