Розробка проекту з математики у 5, 7, 8 класах на тему: «Геометрія на службі у людини»

Про матеріал

Заохочуйте бажання дітей до оновлення,

якщо ви хочете виховати в них риси

нової людини.

Ш. Амонашвілі

У наш час розвиток суспільства міцно пов'язаний із проектною культурою у сфері матеріального виробництва, науки, мистецтва, системи соціальних відносин.

Сучасна школа повинна навчити учнів адаптуватися до соціальних змін і криз у суспільстві, бути психологічно стійкими, розвивати здатність до самоорганізації, відчувати себе впевненими на ринку праці. Для цього навчальний заклад (вчителі, вихователі) повинен забезпечувати високий рівень знань випускників, уміння самостійно набувати знання та застосовувати їх на практиці, розвивати кожного учня як особистість, здатну до практичної роботи, формувати навички пізнавальної й дослідницької діяльності, грамотно працювати з інформацією, спілкуватися з однолітками та дорослими.

Часто на уроках математики можна почути від учнів таке: «Хто це придумав?», «Навіщо треба знати цю тему?», «Мені математика не знадобиться у житті». Як знайти на це правильні відповіді?

Перший крок у цьому напрямі − нешаблонний, нетрадиційний підхід до навчання. Основою для такого кроку є технологія особистісно орієнтовного підходу в навчанні. Одним із успішних методів реалізації особистісно орієнтовного навчання є метод проектів.

Перегляд файлу

Розробка проекту з математики у 5, 7, 8 класах на тему: «Геометрія на службі у людини»

Заохочуйте бажання дітей до оновлення,

якщо ви хочете виховати в них риси

нової людини.

Ш. Амонашвілі

У наш час розвиток суспільства міцно пов’язаний із проектною культурою у сфері матеріального виробництва, науки, мистецтва, системи соціальних відносин.

Проектна діяльність дає учням змогу планувати свою роботу, попередньо прораховуючи можливі результати, використовувати багато джерел інформації, самостійно збирати і накопичувати матеріал, аргументувати свою думку, приймати рішення, установлювати соціальні контакти, оцінювати себе та інших.

Сьогодні метод проектів − один із перспективних видів навчання, тому що він створює умови для творчої самореалізації учнів, підвищує мотивацію для отримання знань, сприяє розвитку інтелектуальних здібностей. Учні набувають досвіду вирішення реальних проблем з огляду на майбутнє самостійне життя [10].

Основним орієнтиром змісту модернізації навчання має стати особистість, що інтенсивно розвивається. Саме тому метод проектів є один із ефективних видів виховання. Проектна діяльність передбачає роботу в колективі. Така ситуація формує соціальну особистість. Працюючи у команді, діти вчаться взаємодіяти один з одним, вирішувати важливі конфлікти, набувати навичок етичного міжособистісного спілкування, брати відповідальність за вибір рішення. Становленню особистості сприяє також необхідність допомогти один одному, оцінювати один одного, критикувати, а найголовніше − нести відповідальність за свою роботу перед собою, своєю групою, всім класом.

Таким чином, суть проектної діяльності – стимулювання інтересу як в учнів так і у вчителів до певних проблем, що зумовлює володіння визначеною сумою знань. Метод проектів передбачає розв’язання однієї або декількох проблем, дозволяє практично їх застосовувати, ідучи від теорії до практики. Результатом моєї навчально-методичної роботи є наступний проект за даною технологією.

План навчального проекту

Автор навчального проекту
Прізвище, ім’я, по батькові	Коровкіна Ірина Сергіївна
Назва навчального закладу	Іванівський навчально–виховний комплекс Чугуївського району Харківської області
Учасники проекту. Учні 5-го, 7-го, 8-го класів
Опис проекту
Назва проекту	Геометрія на службі у людини
Основні питання
Ключове питання	Чи варто вчити геометрію?
Тематичні питання	1.Для чого потрібно вивчати геометрію? 2.Де можна використати знання з геометрії в повсякденному житті? 3.Чи стикаєшся ти в повсякденному житті з математичними моделями задач?
Змістовні питання	Для учнів 5-го класу. 1.Які просторові фігури ви знаєте? 2.За якою формулою можна обчислити об’єм прямокутного паралелепіпеда? Для учнів 7-го класу 1.Дайте означення рівнобедреного трикутника. 2.Сформулюйте властивості рівнобедреного трикутника. 3.Скільки ознак рівності трикутників ви знаєте? Сформулюйте їх. Для учнів 8-го класу 1.Які трикутники називаються подібними? 2.Сформулюйте ознаку подібності трикутників за трьома сторонами. 3.Сформулюйте ознаку подібності трикутників за двома кутами. 4.Сформулюйте ознаку подібності за двома сторонами і кутом між ними.

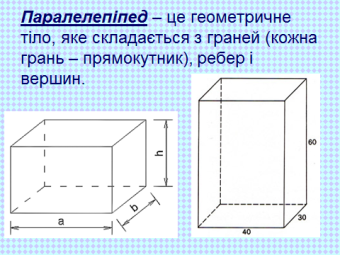
Стислий опис проекту. Проект реалізується в рамках курсу математики 5-го класу та геометрії 7-го і 8-го класів. Проект «Геометрія на службі у людини» стосується тем «Прямокутний паралелепіпед, його виміри» (5кл.), «Об’єм прямокутного паралелепіпеда» (5кл), розділу «Трикутники» (7кл.), розділу «Подібність трикутників» (8кл.). Проект включає дослідницький та інформаційний блоки. У позаурочний час учні, об’єднавшись у групи (по бажанню індивідуально), збирають необхідний матеріал, класифікують його, розподіляють за категоріями,проводять дослідницьку діяльність, аналіз розв’язання проблеми.Вони будуть виконувати різні види робіт: створювати і обговорювати презентації, писати реферати і повідомлення з історії, що пов’язані з математикою, розв’язувати задачі практичного змісту.

Відповідно до програми вчитель проводить мотивацію з урахуванням особистісного життєвого досвіду учнів шляхом зацікавлення задачами, історичними фактами тощо. У ході підготовки учнівських проектів учитель викладає теоретичний матеріал, розробляє систему задач, що необхідно розв’язати, консультує, допомагає учням.

Навчальні предмети, з якими пов’язаний навчальний проект: математика, геометрія, біологія, фізика, інформатика, географія, технології, астрономія, ОБЖ.

Результати проекту учні можуть подавати у вигляді презентації, публікації, веб-сторінки, плакату, доповіді, реферату, проспекту, журналу тощо.

Мета проекту: формувати знання учнів про прямокутний паралелепіпед, трикутники,подібність трикутників, вдосконалити навички розв’язання задач із вище вказаних тем; розвивати творчу активність учнів, комунікативну компетентність, створювати умови для вияву ініціативи під час роботи над проектом; виховувати в учнів прагнення до самовдосконалення, розвивати інтерес до вивчення математики.

Очікувані результати

Учні під час виконання проекту формують навички:

розв’язання задач практичного змісту;
знаходження та опрацьовування інформації з використанням Інтернету та інших джерел;
праці в групі над розв’язанням спільної проблеми;
чіткого формулювання думок;
здобуття знань і досвіду, необхідних для подальшого життя.

Учитель має можливість:

підвищити інтерес учнів до вивчення предмету;
здійснити об’єктивне оцінювання учнів у різних видах діяльності;
розкрити творчий потенціал кожного учня.

Орієнтовний час, необхідний для виконання роботи: 5клас − 4 тижні; 7 та 8 класи − 6 тижнів.

Вихідні знання та навички (результати діяльності учнів): під час роботи над проектом учні досконало оволодіють поняттями з тем: «Прямокутний паралелепіпед, його виміри», «Об’єм прямокутного паралелепіпеда», «Трикутник», «Подібність трикутників», навчаться розв’язувати задачі на обчислення. Виконання цього виду роботи сприяє кращому засвоєнню навчального матеріалу, активізації пізнавальної діяльності учнів, розвитку дивергентного мислення.

Матеріали та ресурси

Обладнання: принтер, засоби для зв’язку з Інтернетом, проектор, сканер, комп’ютери.

Програмове забезпечення: програми для створення мультимедійних презентацій, програми для створення публікацій, програми для створення веб−сайтів.

Додаткове приладдя та допоміжні матеріали:папір, диски.

Ресурси Інтернету: використовується мережа навчально−виховного комплексу.

Критерії оцінювання остаточних продуктів проекту

	Максимум балів	Оцінювання учнями	Оцінювання вчителем
Актуальність вибраної теми	5
Глибина знань проблеми	5
Повнота та доступність розкриття теоретичного матеріалу	10
Чіткість поданого практичного дослідження	10
Наявність матеріалів з історії розвитку предмета	5
Чіткість, точність, охайність виконаних графіків, таблиць	10
Наявність власноруч створених схем, діаграм	10
Розробка кросворду, цікавих задач	10
Наявність цитат, віршів про об’єкт дослідження	10
Представлення презентації	10
Створення слайду	10
Зрозумілість викладеного матеріалу	5
Обґрунтованість висновків, що базуються на наведених даних	10
Чіткість і доступність виступу	5
Зовнішня привабливість, грамотність	5
Усього балів Остаточна оцінка	120

Примітка. Кожний вид звіту має бути переглянутий та оцінений іншими учнями і вчителем; для отримання остаточної оцінки, кількість набраних балів розділити на 10.

Робота над проектом

Перед початком роботи над проектом учні переглядають презентацію вчителя, з якої вони дізнаються про проект, його мету та завдання.
Учні об’єднуються у групи, розподіляють між групами поставлене вчителем завдання, обговорюють проблему та шляхи її розв’язання.
Кожна група в процесі підготовки проекту обирає конкретне завдання та вид звіту, складає план роботи, пропонує порядок виступів, виходячи з логіки вивчення теми.

5 клас

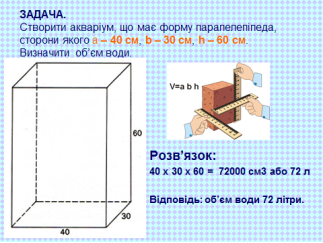
Учитель. Перед вами, учнями 5−го класу, ставиться завдання: самостійно облаштувати шкільний акваріум. Для цього необхідно знати його виміри, обчислити об’єм. Ознайомитися з потребами різних видів рибок, переконатися в їх сумісності та визначити об’єм необхідної води. Розрахувати вартість витрат на влаштування акваріуму.

Пропоную скласти дві групи: біологи та математики.

Біологи

1.Проводять опитування:«Яких рибок ти хотів би бачити у шкільному акваріумі?».

2.З’ясовують необхідний об’єм життєвого простору для різних видів рибок.

Математики

1.Визначають розміри та об’єм акваріума.

2.Відповідно до інформації, отриманої від біологів, переконуються в достатності його об’єму.

3.Обчислюють кошторис для влаштування шкільного акваріуму.

По завершенню проекту на наступному уроці учням можна запропонувати виконати контрольну роботу у вигляді тестових завдань та задач.

Тестові завдання до теми «Прямокутний паралелепіпед. Об’єм прямокутного паралелепіпеда»

Скільки ребер у прямокутного паралелепіпеда?

А)6; б)12; в)24.

2. Скільки вершин у прямокутного паралелепіпеда?

А)4; б)8; в)12.

3. Скільки граней у прямокутного паралелепіпеда?

А)4; б)6; в)8.

4. Якою буквою позначають об’єм?

А)Р; б)S; в)V.

5. Виберіть серед наведених формулу, за якою обчислюється об’єм куба:

A)S=a²; б)V=a³; в)Р=4а.

6. Скільки потрібно кубиків, ребро яких 1см, щоб скласти кубик, ребро якого2см?

А)4; б)8; в)12.

7. Об’єм прямокутного паралелепіпеда з вимірами 4дм, 6дм і 5дм дорівнює …

А)12дм³; б)120дм³; в)60дм³.

8. Якою із запропонованих формул потрібно скористатися, щоб знайти довжину всіх ребер куба?

A)d=4a; б)d=12a; в)d=18a.

9.Об’єм куба з ребром 4см дорівнює… .

А)16см³; б)8см³; в)64см³.

10.Об’єм прямокутного паралелепіпеда дорівнює 240см³. Яка з наступних трійок чисел може задавати виміри цього паралелепіпеда:

А)4см; 6см;12см; б)5см; 6см; 8см; в)3см; 5см; 10см?

11. Ребро куба дорівнює 3см. Площа поверхні куба дорівнює… .

А)27см²; б)36см²; в)48см².

12. Площа поверхні прямокутного паралелепіпеда, який має виміри 4м, 6м і 5м дорівнює… .

А)120м²; б)60м²; в)100м².

Задачі до теми «Прямокутний паралелепіпед. Об’єм прямокутного паралелепіпеда»

1.Одним шаром паперу обклеїли куб, довжина ребра якого дорівнює 3дм. Скільки квадратних дециметрів паперу пішло на обклеювання куба?

2.Скільки дроту пішло на виготовлення дротяного каркаса прямокутного паралелепіпеда, виміри якого дорівнюють 3 дм, 5 дм і 6 дм?

3.Рулон шпалер має ширину 50 см і довжину 10 м. Необхідно обклеїти стіни в кімнаті, розмір якої 4м x 4м x 2,5м. Загальна площа вікна і дверей 4м². Скільки рулонів шпалер потрібно купити?

4.Скільки пшениці можна засипати в бункер, який має форму прямокутного паралелепіпеда, якщо його довжина дорівнює 8м, ширина−2м, висота−10дм, а маса 1м³ зерна становить 8ц?

5.Об’єм кімнати дорівнює 144м³, а висота−4м. Знайдіть площу підлоги.

6.Площа підлоги спортивного залу дорівнює 192м², а його об’єм−960м³. Знайдіть висоту залу.

Висновок по 5−му класу

Отже, робота над проектом вимагає наявності відповідних навичок і вмінь в учнів, а саме самостійного конструювання знань. П’ятикласникам не вистачило цього уміння. Самостійно знайти інформацію, систематизувати її, проаналізувати, опрацювати проблемні питання змогли лише кращі учні.

Зразок учнівського проекту

Слайд 1 Слайд 2

Слайд 3 Слайд 4

Слайд 5 Слайд 6

Слайд 7 Слайд 8

Слайд 9 Слайд 10

7клас

Учитель. Математика − невичерпана, багатогранна наука. Діапазон застосувань математики у різних сферах діяльності людини дуже широкий.

Геометрія − це маленька, невід’ємна частинка математики, яка допомагає нам у пізнанні навколишнього середовища. Геометрія завжди мала численні практичні застосування. Основними її споживачами були землеміри, ремісники, будівельники, художники. Землемірам потрібні були правила вимірювання ділянок. Ремісники користувались поняттями про геометричні фігури та форми. Будівельники, користуючись геометрією, креслили план споруди. Завдання художників було складнішим: їм потрібно було відтворювати на двовимірній площині те, що відбувається в тривимірному просторі.

Геометрія, у перекладі українською, означає землемірство. Така назва зумовлена тим, що зародження геометрії пов’язане з вимірюваннями на місцевості, тобто з практичною діяльністю людства.

У наш час знання з геометрії потрібні будівельнику, архітектору, геодезисту, інженеру, художнику, робітнику. Виконуючи цей проект, переконаємось в цьому. Для подальшої роботи сформуємо три групи: історики, теоретики, практики. Кожна група буде досліджувати відповідне питання:

історики «Як виникла геометрія»;
теоретики «Геометрія − наука про властивості фігур»;
практики «Застосуємо на практиці».

Звіт першої творчої групи

Презентація учасників проекту.

Слайд 1 Слайд 2

Слайд 3 Слайд 4

Слайд 5 Слайд 6

Слайд 7 Слайд 8

Слайд 9 Слайд 10

Слайд 11

Повідомлення «Як виникла геометрія».

Геометрія є однією з найбільш давніх математичних наук. Історія людства налічує 2 мільйони років. Уже первісним людям доводилося лічити: треба було визначити, скільки людей в тій чи іншій групі, давати кількісну оцінку здобичі (м’яса, риби,плодів, поживних коренів тощо).

Не могли люди не звернути увагу також і на форми речей. За формою і кольором вони розрізняли породи дерев придатні для будівництва від тих, що тільки на дрова, смачні горіхи від гірких і т. д. Особливо смачними їм здавались горіхи кокосової пальми. Ці горіхи дуже схожі на кулю. А добуваючи кам’яну сіль, люди натрапляли на кристали, що мали форму куба.

Щоб виготовити наконечник стріли або списа, видовбати човен із стовбура, треба було придивлятися до відповідних форм камінців, стовбурів дерев тощо.

Уже 20 тисяч років тому назад були виготовлені знаряддя досить правильної геометричної форми, а потім люди навчилися їх шліфувати. Відшліфовані знаряддя дозволяли швидше вести рубку ліса, розрізати м’ясо, краще полювати на звірів. Спеціальних назв для геометричних фігур спочатку, звичайно, не було. Говорили: «такий же, як кокосовий горіх» або «такий же, як сіль» тощо. Таким чином, фіксуючи найприйнятніші форми, люди навчилися виготовляти пристосування для роботи і полювання, посуд, обладнувати житло.

А коли люди почали будувати будівлі із дерева, прийшлось краще розібратись в тому, якої форми слід надавати стінам і покрівлі, якої форми повинні бути дерев’яні колоди і т. д. Стало ясно, наприклад, що не обтесуючи дерев’яні колоди, дім з них не побудуєш: вони будуть котитися. А покрівля повинна бути похилою, щоб з неї стікав дощ. І, самі того не знаючи, весь час вони займалися геометрією. Тільки слово «геометрія» тоді не існувало, а форми тіл ще не розглядались окремо від інших їх властивостей.

З розвитком людського суспільства нагромаджувалися знання про форми і властивості цих форм, що сприяло удосконаленню трудових процесів, пов’язаних з будівництвом каналів, городищ і різних за призначенням великих споруд. Коли почали будувати кам’яні будівлі, прийшлося переносити важкий камінь. І було помічено, що перекатувати важкий камінь стає легшим, якщо для катка взяти пряме дерево і від нього відрізати шматок з майже однаковою товщиною на початку і кінці. Так люди познайомились з однією із найважливіших фігур – циліндром. Перевозити вантажі на катках було досить тяжко, тому що самі дерев’яні стовбури важили багато. Щоб полегшити роботу, стали вирізати із стовбурів тонкі круглі пластинки і за їх допомогою переносити вантажі. Так з’явилося колесо. Це було прекрасне відкриття. Першовідкривач колеса дійсно зробив велику справу. Воїни на бойових колісницях легко перемагали піших воїнів.

Давно вже люди помітили, що глина не пропускає воду. Із неї ліпили горшки та інший посуд. Проте глина була дуже м’якою і неміцною. Але одного разу,поставивши горщок на вогонь, первісна людина помітила, що посуд став твердим і міцним. До нас дійшли уламки древньої глиняної посуди, за якими можна бачити, як краще і краще опановувала людина різні геометричні форми. І от настав день, коли був виготовлений перший гончарний круг. На ньому уже можна було придавати посуду округлену форму. І не випадково поети порівнювали із гончарним кругом обертання небесного круга.

Перехід до осідлого землеробства висунув проблему вимірювання земельних ділянок. З’явилися й перші фахівці у цій галузі – землеміри. Щоб краще виконувати свої професійні завдання, вони змушені були виявляти і вивчати властивості різних форм та фігур. Геометрична форма селянських полів була різноманітною. Для того щоб збирати податки,треба було знати їх площі. Астрономам, які спостерігали за небом і давали на основі цих спостережень вказівки, коли починати польові роботи, повинні були визначати положення зірок на небі. Для цього потрібно виміряти кути. Так практична діяльність людини привела в майбутньому до поглиблення знань про форми фігур, розвитку геометрії. Люди стали вчитися виміряти і площі, і об’єми, і довжини.

Грандіозні єгипетські піраміди, дивовижні споруди в Америці, Індії, Китаї, багатьом з яких по кілька тисяч років, свідчать, що вже в сиву давнину люди багато знали про форми речей і вміло використовували ці знання. Ще в давніх вавилонських клинописних таблицях і єгипетських папірусах знаходять перші геометричні факти. Проте це ще не були наукові знання.

Слово «геометрія» з’явилося пізніше, як відомо воно грецького походження, що в буквальному перекладі означає «землю міряти». Головну роль у розвитку геометрії зіграли практичні задачі, що було зібрано у перші посібники для вивчення математики. Але в цих посібниках були вказівки як знайти невідоме число – кількість речей, відстань, час, площу і т.п. І зовсім не пояснювалося, чому слід робити саме так, а не інакше. Просто подавався зразок, за яким треба було розв’язати аналогічні задачі. Про це й писав грецький вчений Едем Родоський (IV ст. до н. е.): «Геометрія була відкрита єгиптянами і виникла при вимірюванні землі. Це вимірювання було їм необхідно внаслідок розливу ріки Нілу, що постійно змивав межі. Нема нічого дивного в тому, що ця наука, як і інші, виникла із необхідності людини».

Звичайно, не можна думати, що якщо б не було Нілу з його сильними розливами, не було б і геометрії. Людям потрібно визначати відстані між точками, площі земельних ділянок і об’єми тіл, і вони створювали б геометрію не в Єгипті, так у Греції, не в Індії, так у Китаї. Так воно і було.

Геометрія стала наукою лише в VII – VI століттях до н. е., з того часу, коли в ній почали не лише описувати фігури та їх властивості, а й обґрунтовувати наявність цих властивостей, доводити правильність висловлених про ці фігури тверджень. Тепер становище докорінно змінилося: на перше місце висувається обґрунтування правильності розв’язування, доведення. За 600 років до н. е. такий підручник з геометрії нового типу написав грецький учений Фалес Мілетський (640 – 548 до н. е.). Він був філософом – матеріалістом, астрономом і математиком, його вважали одним з найвидатніших мудреців стародавніх часів,двічі нагороджували золотою триногою як наймудрішого з еллінів. Підручник Фалеса був невеликим за обсягом, але саме з нього починається історія геометрії як науки. Кожне твердження про геометричні фігури він обґрунтовує. Відтоді математики саме так оформлюють свої міркування. Через це Фалеса з повною підставою називають батьком геометрії.

Автор біографій багатьох видатних діячів стародавніх часів Плутарх писав, що Фалес був єдиним ученим, який у своїх дослідженнях «пішов далі того, що було необхідним для практичних потреб».

Серед учених – геометрів особливе місце належить грецькому математику Евкліду (IV – III ст. до н. е.).

Усний журнал «Геометрія Евкліда».

Сторінка 1 «Евклід – колумб геометрії»

Дуже багато для створення геометрії як науки зробив грецький математик Евклід, який жив у III ст. до нашої ери. Він звів набуті на той час геометричні знання в струнку систему і виклав їх у тринадцяти книгах, які назвав «Начала».

Про Евкліда відомо дуже мало. Все-таки в нас немає підстав сумніватися в існуванні Евкліда, тим більше що в цьому не сумнівалися й пізніші грецькі вчені, дещо розповідавші про нього. Папп Олександрійський (III в.) повідомляє, що він був дуже доброзичливий до всіх тих, хто зробив хоч який-небудь внесок у математику, коректний, найвищою мірою порядний і зовсім позбавлений марнославства.

Евклід родом з Афін, був учнем Платона. Автор найдавніших трактатів з математики, що дійшли до сьогодення. В них підсумовано досягнення давньогрецької математики. Наукова діяльність Евкліда проходила в Александрійській бібліотеці — суспільній інституції, що являла собою бібліотечний, науковий, навчальний, інформаційно-аналітичний, і культурологічний комплекс.

Основна праця Евкліда «Начала» (латинізована назва «Елементи») включає в себе 13 книжок, у яких міститься систематизований виклад геометрії, а також деяких питань теорії чисел.

«Начала» відіграли винятково важливу

роль у подальшому розвитку математичної науки. Історичне значення цієї праці полягає в тому, що в ній уперше здійснено спробу логічної побудови геометрії на основі аксіоматики.

«Начала» Евкліда витримали понад 500 перевидань усіма мовами світу. Мав також роботи з астрономії, оптики, теорії музики.

Сторінка 2 ««Начала» начал»

Основний твір Евкліда називається «Начала». Книги з такою ж назвою, в яких послідовно викладалися всі основні факти геометрії і теоретичної арифметики, складалися раніше Гіппократом Хіосським, Леонтом і Февдієм. Проте «Начала» Евкліда витіснили всі ці твори з ужитку і протягом більш ніж двох тисячоліть залишалися базовим підручником геометрії. Створюючи свій підручник, Евклід включив в нього багато з того, що було створене його попередниками, обробивши цей матеріал і звівши його воєдино.

«Начала» складаються з тринадцяти книг. Перша і деякі інші книги передують списком визначень. Першій книзі передує також список постулатів і аксіом. Як правило, постулати задають базові побудови (наприклад, «потрібно, щоб через будь-які дві точки можна було провести пряму»), а аксіоми — загальні правила виведення при операції з величинами (наприклад, «якщо дві величини дорівнють третій, вони рівні між собою»). З сучасної точки зору, різниці між постулатами і аксіомами нема.

У I книзі вивчаються властивості трикутників і паралелограмів; цю книгу вінчає знаменита теорема Піфагора для прямокутних трикутників. Книга II, виходить від піфагорійців, присвячена так званій «геометричній алгебрі». У III і IV книгах висловлюється геометрія кіл, а також вписаних і описаних багатокутників; при роботі над цими книгами Евклід міг скористатися творами Гіппократа Хіосського. У V книзі вводиться загальна теорія пропорцій, побудована ЕвдоксомКнідським, а в VI книзі вона додається до теорії подібних фігур. VII—IX книги присвячені теорії чисел і знов посилаються до піфагорійців; автором VIII книги, можливо, був АрхітТарентський. У цих книгах розглядаються теореми про пропорції і геометричні прогресії, вводиться метод для знаходження найбільшого загального дільника двох чисел (відомий нині як алгоритм Евкліда), будується парні довершені числа, доводиться нескінченність множини простих чисел. У X книзі, що є найоб'ємнішою і найскладнішою частиною «Начал», будується класифікація ірраціональностей; можливо, що її автором є Теєтет Афінський. XI книга містить основи стереометрії. У XII книзі за допомогою методу вичерпання доводяться теореми про співвідношення площ кіл, а також об'ємів пірамід і конусів; автором цієї книги за загальним визнанням є ЕвдоксКнідський. Нарешті, XIII книгу присвячено побудові п'яти правильних багатогранників; вважається, що частина побудов була розроблена Теєтетом Афінським.

У рукописах, що дійшли до нас, до цих тринадцяти книг додані ще дві. XIV книга належить александрійцуГипсиклу (біля 200 р. до н. е.), а XV книгу створено під час життя Ісідора Мілетського, будівельника храму св. Софії в Константинополі (початок VI ст. н. е.).

«Начала» надають загальну основу для подальших геометричних трактатів Архімеда, Аполлонія і інших античних авторів; доведені в них припущення вважаються загальновідомими. Коментарі до «Начал» в античності складали Герон, Порфирій, Папп, Прокл, Симплікій. Зберігся коментар Прокла до I книги, а також коментар Паппа до X книги (у арабському перекладі). Від античних авторів коментаторська традиція переходить до арабів, а потім і до Середньовічної Європи.

У створенні і розвитку науки Нового часу «Начала» також зіграли важливу ідейну роль. Вони залишалися зразком математичного трактату, що строго і систематично висловлює основні положення тієї або іншої математичної науки.

Сторінка 3 «Евклідові цікавинки»

Афоризми, цитати, вислови, фрази Евкліда

Що й потрібно було довести.

Немає царського шляху до геометрії.

Якщо теорему так і не змогли довести, вона стає аксіомою.

Те, що прийнято без доказів, може бути відкинуто без доказів.

При деяких незвичайних і досить таємничих обставинах окремі парні числа ведуть себе як непарні.

Для тирана і для могутнього міста, пануючого над іншими містами, все, що вигідно, то і розумно.

Як-то раз давньогрецького геометра Евкліда запитали: – Що б ти хотів з’їсти– цілихдва яблука або чотири половинки? – Звичайно, чотири половинки. – А чому? Адже це одне і те ж. – Аж ніяк. Вибираючи два цілих яблука, як я дізнаюся, червиві вони чи ні?

Звіт другої творчої групи

За словами ДавідаГільберта:«у величезному саду геометрії кожен може підібрати собі букет за смаком». Результатом нашого дослідження став рівнобедрений трикутник. Ми працювали над питаннями:

1). Що знали про трикутник в далеку давнину?

2). Означення та основні властивості рівнобедреного трикутника.

3). Задачі, які приводять до поняття «золотого» трикутника.

4). Визначення властивостей «золотого» трикутника.

5). Застосування правила «золотого» трикутника.

Девізом своєї роботи обрали слова Піфагора«Тимчасова невдача краще тимчасової удачі».

1). Що знали про трикутник в далеку давнину?

У Стародавній Греції трикутник вважали однією з основних геометричних фігур. Слово «трикутник» античного походження. Знак для позначення трикутника застосував ще в І ст. давногрецький учений Герон. Знак застосовувати в IV ст.

Уже кілька тисяч років єгиптяни знали,що коли сторони трикутника дорівнюють 3, 4 і 5 одиничним відрізкам, то такий трикутник прямокутний. Тому землеміри Стародавнього Єгипту для побудови прямого кута чинили так. Мотузок ділили вузлами на 12 рівних частин і кінці зв’язували. Потім мотузок натягували на землі так, щоб утворився трикутник із сторонами 3, 4 і 5 поділок.

Кут трикутника, протилежний стороні, що має 5 поділок, був прямий, (3²+4²=5²). Тому прямокутний трикутник із сторонами 3, 4, 5 одиниць називають єгипетським.

Ребра бічних граней єгипетських пірамід утворюють майже рівносторонні трикутники.

Про ці факти ми дізналися з підручника геометрії для 7 класу (автори Бурда М.І., Тарасенкова Н.А.). Г. Апостолова у підручнику геометрії для 8 класу описує наступне:

«За часів Паскаля (XVI ст.) математику найчастіше називали геометрією. Якось дванадцятирічний Блез Паскаль запитав у батька, Етьєна Паскаля, що таке «геометрія». Етьєн Паскаль, не надаючи своїм словам особливого значення, сказав, що геометрія – це така собі теорія, що вивчає способи креслення фігур і вказує співвідношення між їх елементами. Через деякий час батько побачив, що син зосереджено розмірковує над складеними з паличок трикутниками. Як з’ясувалося, Блез якраз додумував доведення відкритого ним цікавого факту: у будь − якому трикутнику сума всіх трьох кутів разом складає два прямі кути. Тоді Етьєн відімкнув шафу з книгами і дав Блезу «Начала» Евкліда. Тринадцятирічний Блез опанував її як захоплюючий роман. Невдовзі Блеза Паскаля допустили до засідань наукового паризького гуртка (пізніше на базі цього гуртка було створено Паризьку академію наук)».

2). Означення та основні властивості рівнобедреного трикутника

Трикутник називається рівнобедреним, якщо дві його сторони рівні.

Рівні сторони рівнобедреного трикутника називають бічними сторонами, а третю його сторону – основою.

АВ, ВС – бічні сторони, АС – основа.

Теорема (властивості рівнобедреного трикутника).

1) бісектриса, проведена до основи, є медіаною й висотою; 2) кути при основі рівні.

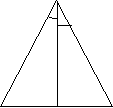Дано: АВ=ВС, BD – бісектриса,

Довести: 1) AD=DC, BDAC; 2) C.

Доведення. Нехай АВС − рівнобедрений, у якому проведено бісектрису BD. Розглянемо У них: АВ=ВС за умовою, BD – спільна сторона, , оскільки BD бісектриса АВС. Отже, = за двома сторонами і кутом між ними.

З рівності трикутників ABD i CBD випливає рівність їх відповідних сторін і кутів:

AD=DC, тобто BD – медіана АВС. Оскільки ці

кути суміжні й рівні, то вони прямі. Отже, BD AC, тому BD – висота

А =

Довели, що в рівнобедреному трикутнику бісектриса, медіана і висота,

проведені до основи, збігаються. Тому справедливі також твердження:

висота рівнобедреного трикутника, проведена до основи, є медіаною і бісектрисою;
медіана рівнобедреного трикутника, проведена до основи, є висотою і бісектрисою.

Задача. Доведіть, що в рівнобедреному трикутнику медіани, проведені до бічних сторін, рівні.

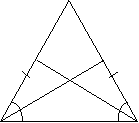B Дано:АВС – рівнобедрений, АВ = ВС,

АМ, CN – медіани, AN = NB, BM =MC.

Довести: АМ =NC.

NM Доведення(1 спосіб). Розглянемо

АС – спільна сторона, за властивістю

рівнобедреного трикутника, AN = AB = BC = CM

A C за умовою задачі. Отже, за двома

сторонами і кутом між ними. З рівності трикутників випливає, що АМ = CN.

Доведення (2 спосіб)

Розглянемо АВ = СВ за умовою задачі,

ВМ = ВС = АВ = BN. Отже, за двома сторонами і кутом між ними. З рівності трикутників випливає, що AM = CN. Отже,

в рівнобедреному трикутнику медіани, проведені до бічних сторін, рівні.

Теорема (ознака рівнобедреного трикутника). Якщо в трикутнику два кути рівні, то він рівнобедрений.

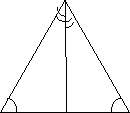Дано: ,

Довести: АВ = ВС.

Доведення. У АВС проведемо бісектрису BD.

Тоді . Розглянемо

У них BD – спільна сторона. Оскільки

А D C за умовою, за побудовою, то рівні й треті кути: Отже, за стороною і прилеглими до неї кутами. З рівності цих трикутників випливає, що АВ =ВС.

З доведених властивостей й ознаки рівнобедреного трикутника випливає, що

у трикутнику проти рівних сторін лежать рівні кути і, навпаки, проти рівних кутів – рівні сторони.

Задачі, які приводять до поняття «золотого» трикутника

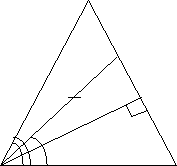B Задача 1. Кут при основі рівнобедреного

трикутника у 2 рази більший, ніж кут при

M вершині. Знайти кути цього трикутника.

D Розв’язання. Нехай у АВС АВ = ВС,

у 2 рази більший, ніж Тоді

⁰, = (2х)⁰. За теоремою про

суму кутів трикутника маємо рівняння:

A C х+2х+2х=180,

(мал.) 5х=180,

х=,

х=36.

Отже, ⁰, ⁰ = 72⁰.

Відповідь: 72⁰, 36⁰, 72⁰.

Задача 2. Висота, проведена до бічної сторони рівнобедреного трикутника, поділяє навпіл кут між основою та бісектрисою кута при основі. Знайти кути цього трикутника (див. мал.).

Розв’язання. Нехай у АВС АВ = ВС, АМ – бісектриса, тому ADAD – бісектриса тому

Нехай ⁰, тоді ⁰-x⁰, ⁰-2x⁰,

360⁰ – (4x)⁰, , тому маємо рівняння:

360 – 4х = х,

5х = 360,

х= ,

х = 72.

Отже, 72⁰, 180⁰ - 2x72⁰ =36⁰.

Відповідь: 72⁰, 36⁰, 72⁰.

Зауваження.– прямокутні. за катетом AD і гострим кутом ( АС = АМ.

Трикутник, який розглядався в задачах, особливий, він отримав назву «золотого» трикутника.

4). Визначення властивостей «золотого» трикутника

Користуючись розв’язаними задачами, встановлюємо, що «золотий» трикутник – це такий рівнобедрений трикутник, у якого:

кут при основі в два рази більший, ніж кут при вершині (відповідні величини цих кутів – 72⁰ і 36⁰);
висота, проведена до бічної сторони, поділяє навпіл кут між основою та бісектрисою кута при основі;
бісектриса кута при основі дорівнює цій основі.

5). Застосування правила «золотого» трикутника

Правило «золотого» трикутника широко використовують майстри живопису для визначення взаємного розташування елементів картин. Згадаємо відомий у всьому світі портрет Мона Лізи («Джоконди»), автором якого є талановитий італійський живописець і вчений епохи Відродження Леонардо да Вінчі (1452 – 1519).

Він вважав, що ідеальні пропорціїлюдського тіла повинні бути пов’язані з золотим перерізом,тобто з поділомвідрізка на дві частини, при якому більша частина так відноситься до всьоговідрізка, як менша частина до більшої. Цей термін вперше ввів Леонардо да Вінчі.

Описание: http://rudocs.exdat.com/pars_docs/tw_refs/174/173167/173167_html_m5d48ad3.jpg

Шедевр великого художника відрізняється своєю неповторною виразністю, загадковістю та прихованими таємницями. Композиція картини ґрунтується на «золотих» трикутниках. Це довели дослідники творчості да Вінчі.

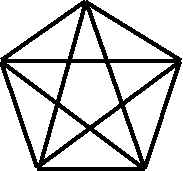У відомого математика Піфагора була своя школа. Учнів цієї школи називали піфагорійцями. Емблемою союзу і розпізнавальним знаком піфагорійців була пентаграма, яку також називали піфагорійськоюзіркою. Цю фігуру можна отримати, якщо продовжити сторони рівностороннього п’ятикутника до їх взаємного перетину. Піфагорійці використовували цю фігуру, креслячи її на піску, щоб привітати або розпізнати один одного.

Фігура ця справді цікава: вона побудована із «золотих» трикутників, має властивості, які виділяють її серед інших зірок. Знаючи величину кутів «золотого» трикутника, нескладно дійти висновку, що сума гострих кутів при вершинах зірки дорівнює 180⁰ (36⁰x5 = 180⁰). Ще цікавіші властивості мають точки перетину сторін піфагорійської зірки. В усіх точках перетину сторінзірки Піфагора знаходимо золотий переріз, тобто такий поділ відрізка надві частини, при якому увесь відрізок так відноситься до більшої його частини, як більша частина до меншої.

П’ятикутна зірка – пентаграма – завжди привертала увагу людей досконалістю форми. Вона вважалася амулетом здоров’я.

«Зоряними» многокутниками займався відомий польськийматематик Ян Брожек з Кружелува (1585 – 1662).

Народився у родині міщан. Перші знання отримав від батька. У 1604 році вступив до Краківської академії. Уже у 1608 році почав викладати у ній математику, а через два роки отримав титул доктора філософії. У 1611 році отримав чин капелана, що на той час було нормою, з огляду на формулу фінансування професорів релігійними установами.

У 1614 році Брожек став професором кафедри астрології (астрономії). У 1920-23 роках виїхав до Італії, щоб вивчати медицину в Падуї. У той період почав переписуватись з Галілеєм. Вже як доктор медичних наук у 1624 році вернувся до Польщі. Перед виїздом до Падуї і після повернення (імовірно аж до 1630 року) працював у соляних шахтах Велічки і Бохні, займаючись геодезичними вимірами.

У 1625 році виступив на стороні Краківської Академії в гострій суперечці з єзуїтами стосовно автономії вузу. У підтримку навчального закладу та й вищої освіти тогочасної Польщі загалом в тому ж році опубліковує одну з найвидатніших його справ, Gratis, написану в образі сатиричного діалогу проти ордену Єзуїтів. Цей твір є одним із найкращих полемічних творів давньої польської літератури та один з найвизначніших творів європейської антиєзуїтської літератури.

Після охоплення приходу в Міжріччі (1629), у період 1630-36 навчав на кафедрі Теології. У 1635-36 роках викладав у свою чергу геодезію на кафедрі геодезії, заснованої Адамом Стжалке. Займався вимірами в маєтках Славкув і Йодловнік. У 1639 році Брожек сам заснував фонд, метою якого була оплата стипендій студентам, збільшення зарплати професорських кадрів і купівля обладнання для кафедри.

В 1620 р. поїхав у Падую (Італія) вивчати медицину, де в 1624 р. одержав ступінь доктора медицини. Після чого повернувся на батьківщину.

У1636 р. став священником і доктором богослов'я, що дало йому кафедру і навіть ректорство в Краківській Академії. Брожек вирізнявся непересічною вченістю в різних галузях знань.

Творчий доробок:

«Geodesiadistantiarum» (1610);
«Dissertatioastronomica» (1616);
«DissersatiodecometaAstrophili» (1619);
«Dedieruminaequalitate» (1619);
«Arithmeticaintegrorum» (1620);
«Apologjapierwszakalendarz a rzymskiegopowszechnego» (1641);
«ApologiaproAristoteleetEuclide» (1652);
«Denumerisperfectisdisceptatio» (1637);
«Epistolaeadnaturamordinariamfigurarumpleniusintelligendum» (1615);
«PeripatheticusCracowiensis»;
«DelitteraruminPoloniavetustate»;
«SermoinsynodoLuceornensi» (1641).

У наш час п’ятикутна зірка зустрічається на прапорах і гербахбагатьох країн, наприклад

Китаю, США, Сінгапуру, В’єтнаму, Пакистану,Туреччини, Євросоюзу. Головна будівля військового відомства США маєформу пентаграми, тому отримала назву «Пентагон».

Ось такий теоретичний матеріал ми змогли зібрати із різних джерел. Сподіваємось, що він значно допоможе групі практиків.

Звіт третьої творчої групи

Девіз: «Мало знати, слід і застосовувати» (Гете).

Третя група підібрала задачі практичного змісту. Один із учнів нагадує про загальні теоретичні положення, необхідні для розв’язання цих задач:

нерівність трикутника;
сума кутів трикутника;
сума гострих кутів прямокутного трикутника;
ознаки рівності трикутників;
ознаки рівності прямокутних трикутників;
властивість катета, що лежить проти кута 30⁰.

Задача 1. Чи вистачить 12 см дроту, щоб зігнути з нього трикутник, одна зі сторін якого дорівнює: 1) 7 см; 2) 6 см; 3) 5 см ?

Розв’язання. Застосуємо нерівність трикутника (будь-яка сторона трикутника менша від суми двох інших сторін).

Сума двох інших сторін даного трикутника дорівнює 5 см. 7 см > 5 cм. Отже, 12 см дроту не вистачить, щоб зігнути трикутник зі стороною 7 см.
Сума двох інших сторін даного трикутника дорівнює 6 см. 6 см = 6 см.Отже, 12 см дроту не вистачить, щоб зігнути трикутник зі стороною 6 см.
Сума двох інших сторін даного трикутника дорівнює 7 см. 5 см < 7 cм. Отже, 12 см дроту вистачить, щоб зігнути трикутник зі стороною 5 см.

Задача 2. Щоб виміряти на місцевості відстань між двома пунктами А і В, з яких один (пункт В) неприступний, провішують пряму АD, перпендикулярну до АВ. На прямій AD знаходять таку точку С, щоб АСВ = 45⁰. Шукана відстань АВ дорівнює АС. Чому?

Розв’язання. За умовою задачі – прямокутний, С = 45⁰, тому В = 45⁰. Отже, – прямокутний і рівнобедрений, тому АВ = АС.

Задача 3. На малюнку показано, як виміряти відстань між пунктами А і В, між якими не можна пройти по прямій. Поясніть вимірювання.

Розв’язання. На місцевості виміряли АС = CЕ, ВС =

СD, , як вертикальні. Отже,

за двома сторонами і кутом між ними. Тому

відстань АВ дорівнює відстані DE.

Задача 4. На малюнку показано, як виміряти відстань між пунктами А і В, якщо до пункту В підійти не можна (наприклад, ширину річки). Поясніть вимірювання

С D

Розв’язання. Відкладаємо АС = CD. Проводимо DE так, щоб . Проводимо ВЕ так, щоб за стороною і двома прилеглими кутами, тому АВ = DE.

Задача 5. Щоб виміряти на місцевості відстань між пунктами А і В, між якими не можна пройти, виконали таку побудову: АС CD = BC. Тоді шукана відстань АВ дорівнюватиме AD. Чому ?

Розв’язання. За умовою задачі

А AC , CD = BC, тому

В трикутники АВС і ADC прямокутні,

причому ВС = CD, а катет АС

спільний. Отже, трикутники АВС і

С ADC рівні за двома катетами, тому

рівні їх гіпотенузи АВ і AD.

Задача 6. Недалеко від населених пунктів А і В проходить шосе. Потрібно побудувати автобусну зупинку так, щоб відстані від неї до населених пунктів були однакові. Місце зупинки визначили так (див. мал.): знайшли середину D відстані між населеними пунктами. Провісили пряму DC і позначили на цій прямій точку С біля шосе – місце зупинки. Чи правильно визначили місце для автобусної зупинки ? Поясніть.

В Розв’язання. Так правильно. Якщо з’єднати

D точки А і С, В і С отримаємо два рівні

A прямокутні трикутники ADC i BDC (AD = BD,

DC – спільний катет). Отже, АС = ВС.

Задача 7. На малюнку зображено садову хвіртку, яку скоро перекосить. Як прибити планку (дошку), щоб надати міцності хвіртці ? Поясніть.

Розв’язання. Планку треба прибити так, щоб на хвіртці утворилися два трикутники. Це зумовлено жорсткістю трикутника.

Якщо взяти три дерев’яні планки і закріпити їх кінці шпильками або цвяшками так, щоб утворився трикутник, то змінити його форму не можна. Трикутник – фігура жорстка. Це випливає з ознаки рівності трикутників за трьома сторонами. Жорсткість трикутника часто використовують на практиці.

По закінченні проекту учням можна запропонувати для виконання домашню самостійну роботу. Завдання розміщуються на стенді «Сьогодні на уроці». При обговоренні самостійної роботи учням пропонується вибрати свій «математичний маршрут», який складається з таких «ділянок»:

«Повторюємо, закріплюємо» − відповіді на запитання для самоперевірки, позначка запитань цього блоку − ?;
«Обчислюємо» − розв’язування задач на обчислення, позначка – О;
«Доповнюємо теорію» − задачі на встановлення нових теоретичних фактів, позначка – Т;
«Досліджуємо» − прикладні задачі дослідницького характеру, позначка – Д.

Із задач блоків О, Т, Д учні мають обрати по одній задачі (якщо тільки одна задача, то її розв’язати треба всім). Як правило, задачі з непарними номерами – для першого варіанта, а з парними – для другого. Однак, у разі утруднень, учні мають право самостійно проводити заміну всередині блоку (на задачу з іншого варіанта).

?. Запитання для самоперевірки

Які є види трикутників залежно від довжини їх сторін та міри їх кутів?
Як називають сторони рівнобедреного трикутника? Прямокутного трикутника?
Що таке медіана трикутника? Бісектриса? Висота?
Сформулюйте і доведіть теорему про суму кутів трикутника; про властивості зовнішнього кута трикутника.
У чому полягає наслідок із теореми про суму кутів трикутника?
Які властивості має прямокутний трикутник?
Сформулюйте і доведіть теорему про властивості та ознаку рівнобедреного трикутника.
Які дві геометричні фігури називаються рівними?
Сформулюйте і доведіть ознаки рівності трикутників за двома сторонами і кутом між ними; за стороною і прилеглими до неї кутами; за трьома сторонами.
Сформулюйте ознаки рівності прямокутних трикутників.
Чому дорівнюють кути рівностороннього трикутника?
Чому дорівнює сума гострих кутів прямокутного трикутника?
Чому дорівнює гострий кут прямокутного рівнобедреного трикутника?

О. Задачі на обчислення

1. Знайдіть невідомий кут трикутника, якщо два його кути дорівнюють 30⁰ і 70⁰.

2. Обчисли градусну міру кута між бічними сторонами рівнобедреного трикутника, якщо кут при його основі дорівнює 40⁰.

3. Знайдіть кут при основі рівнобедреного трикутника, якщо кут між бічними сторонами дорівнює 30⁰.

4. Один із кутів рівнобедреного трикутника дорівнює 110⁰. Знайти інші кути.

5. Чи існує трикутник з кутами 60⁰, 70⁰, 80⁰ ?

6. Знайдіть кути трикутника, якщо відомо, що вони пропорційні числам 1, 2, 3. Встановіть вид трикутника.

Т. Задачі на встановлення нових теоретичних фактів

40.(підручник, С.111).

Д. Задача. Знайдіть суму кутів A, B, C, D, E п’ятикутної зірки.

В D

A E

Звіт по 7 – му класу

Робота над проектом для учнів 7-го класу починалася як класно – урочна форма навчання, а закінчилася як позаурочна. Об’єм інформації великий для декількох уроків, та й програму навчання вчителю треба виконувати. Ефективність методу проектів зумовлюється тим, що він потребує ретельної підготовки керівника, навчання учнів технології проектної діяльності, озброєння їх дослідницькими навичками, стимулювання творчих здібностей.

Проектування практично допомогло учням усвідомити роль знань і вмінь у житті й навчанні. Знання стали засобом у освіті, допомогли опанувати культурні зразки мислення та математичної мови, дозволили кожному учневі самостійно освоїти нагромадження культури.

8 клас

Учитель. Наше заняття – це творче дослідження, презентація теми «Подібність трикутників», ваша спільна робота над проектом «Геометрія на службі у людини». Наша робота пройде під девізом «Єдиний шлях, який веде до знань – діяльність» (Б. Шоц). Своєю діяльністю будемо закріплювати набуті знання.

Ви не замислювалися над тим, чому математикам не присуджують Нобелівську премію? Тому, що Альфред Нобель, сам будучи хіміком, інженером, винахідником, промисловцем, вважав математику лише інструментом у галузі досліджень для інших наук. Багатьом з вас відомий вислів «Математика – цариця наук». Кілька років тому цю фразу розтлумачили так: «Математика – служниця наук». Своїм проектом продемонструємо, як можна розкрити служіння математики іншим предметам.

Ми з вами закінчуємо вивчення однієї з найцікавіших тем геометрії «Подібність трикутників». Чому найцікавіших? Відповім так. Поняття «подібність» необхідне для засвоєння загальнотехнічних предметів: креслення, технології (побудова креслень деталей і лекал швейних виробів); природничих – біології (визначення пропорції тіла тварин), географії (визначення масштабу карти деякої місцевості), астрономії (визначення розмірів небесних тіл); ОБЖ (визначення відстані до недоступної точки або висоти предмета), у фотосправі (збільшення негатива) тощо. Наш проект підтвердить слова Миколи Яругіна «І математика безмежно різноманітна і міститься в усьому».

Знання ознак подібності трикутників та їх властивостей допомагає в найнесподіваніші моменти,а деколи й рятує життя.

Напередодні кожна група одержала завдання – підготувати проект на певну тему. Ви повинні були підготувати теоретичні відомості з відповідної теми та приклади, що розкривають тему проекту.

Звіт першої творчої групи

Девіз:«Пам’ятайте, якщо хочете навчитися плавати, то сміливо заходьте у воду, а якщо хочете навчитися розв’язувати задачі, то розв’язуйте їх» (Д. Пойа).

Захист проекту«Метод подібності в розв’язуванні геометричних задач»

Задачі на побудову – це особливий клас геометричних задач, що стосується конструктивної геометрії. Задачі на побудову мають свою специфіку. «Інколи розв’язанням може бути побудована фігура, а деколи – записана послідовність дій, що призведе до правильної побудови» (Руденко О.)

У 7 класі ми ознайомилися з елементарними задачами на побудову: поділ заданого відрізка навпіл; поділ заданого кута навпіл; побудова кута, що дорівнює даному; побудова трикутника за трьома заданими сторонами тощо. Ці задачі є аксіомами конструктивної геометрії. Але, окрім аксіом, мають бути методи розв’язування задач на побудову. З 7-го класу нам відомий метод допоміжного трикутника та метод геометричних місць. Темоюнашого дослідження став ще один метод розв’язування задач на побудову –метод подібності.

Метод подібності визначається як використання подібності трикутників, утворених додатковими побудовами. Будь-який метод вимагає певної послідовності дій – алгоритму.

Алгоритм методу подібності

Аналіз умови задачі.
Побудова:

побудувати фігуру, згідно з умовою, подібно до шуканої;
серед багатьох подібних вибрати ту, що повністю відповідає умові.

Доведення.
Дослідження.

У цілому цей алгоритм збігається зі всіма алгоритмами задач на побудову: аналіз, побудова, доведення, дослідження. Перший етап вимагає аналізу умови, другий – побудови відповідно до цієї умови, третій – доведення того, що одержана фігура є шуканою. На останньому етапі потрібно дослідити всі можливості для цієї задачі: чи завжди так буває, чи існують інші можливості.

Задача 1. (Побудова четвертого пропорційного відрізка). Дано три відрізка а, b, c. Побудувати відрізок х, який задовольняє умову =.

B Дано: a, b i c.

Побудувати: х так, щоб .

D Розв’язання.

Побудова. Візьмемо довільний кут О.

На одній із його сторін відкладаємо

O C p A відрізок ОА =а та ОС = с, а на другій

стороні ОВ = b. З’єднаємо точки А і В.

Через точку С проведемо пряму р. Вона перетинає промінь ОВ у точці D. OD – шуканий відрізок.

Доведення. за другою ознакою подібності трикутників ( – спільний, ). Тому , тобто OD = x.

Задача 2. Якщо через точку, що знаходиться всередині кола, проведено хорди, то добуток відрізків кожної із хорд, на які вона поділяється заданою точкою, є величина стала для даного кола.

Розв’язання.

Аналіз умови.

C В

Р D

Через точку Р усередині кола проведемо хорди АВ і СD. Доведемо, щоСР PB.

Доведення. Розглянемо .CPA = (як вертикальні). На дугу AD спираються вписані кути ACD i ABD, тоді вони рівні. Отже, трикутники АСР і DBP подібні за другою ознакою подібності трикутників. Відповідні сторони пропорційні, тобто . Звідси: СP PD = AP

Задачу доведено.

У загальному випадку задача має такий вигляд

(див. мал..): m.

Задача 3. Доведіть, що точка перетину діагоналей трапеції й середини ]ї основ лежать на одній прямій.

B N C

Дано: ABCD – трапеція (AD BC),

BN = NC, NOAD = M.

Довести:AM = MD.

A M D

Доведення

AD BC, BD – січна, тому як внутрішні різносторонні;
як вертикальні;
тже, за двома рівними кутами;
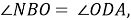
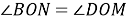
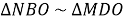
аналогічно: ;
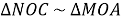
подібність трикутників NBO i MDO, трикутників NOC i MOA дає можливість стверджувати, що

= = , = , BN =NC, тому AM = MD.

Що й треба було довести.

Під час розгляду розв’язку задач виконувалися не всі етапи алгоритму метода подібності. Звертаємо вашу увагу на те, що в задачах на побудову не завжди виконуються всі чотири етапи розв’язування. Інколи можна зупинитися лише на побудові, інколи вистачає тільки доведення.

Звіт другої творчої групи

Девіз: «Предмет математики настільки серйозний, що корисно не пропустити нагоди зробити його цікавішим» (Б. Паскаль).

Захист проекту «Подібність трикутників. Золотий переріз»

З проявами подібності ми часто стикаємося в житті, наприклад, коли розглядаємо на полиці магазину літак – іграшку, подібний до справжнього, або одяг одного фасону, але різних розмірів. Проте перевести наші життєві уявлення про подібність фігур на чітку мову геометрії не надто легко, тому ми почали вивчення властивостей подібності з основної геометричної фігури – з трикутника. Вивчати подібність трикутників без знань теореми про пропорційні відрізки неможливо.

Термін «пропорційний» походить від латинського слова proportionalis, що означає «такий, що має правильне співвідношення між частинами та цілим», «такий, що перебуває в певному відношенні до деякої величини;співрозмірність, певні співвідношення частин між собою».

Вивчення поняття пропорційних відрізків приводить нас до означеннязолотого перерізу.

Золотий переріз – це такий поділ цілого на дві нерівні частини, при якому ціле відноситься до більшої частини так, як більша частина до меншої.

Знайдемо значення такого відношення.

Нехай маємо довільний відрізок АВ і точку С на ньому.

А С В

Якщо точка С ділить цей відрізок за принципом золотого перерізу, то виконується співвідношення:

АВ : АС = АС : СВ.

За такого розміщення точки С на відрізку АВ кажуть, що точка С ділить відрізок АВ у крайньому і середньому відношенні.

Позначимо шукане відношення через х, а довжину АС через а. Тоді

= = х і СВ = , АВ = а + .

Маємо рівняння:

х = 1 + , х² – х – 1 = 0,

D =b² – 4ac = 1 + 4 = 5 >0,

x_1,2 =.

Оскільки х > 0, то умову задовольняє значення

х = .

Саме це число називають золотим перерізом і позначають літерою . Це число ірраціональне і наближено дорівнює 1,61803398.

У геометрії розглядаються поняття: золотий прямокутник та золотий трикутник.

Прямокутник називається золотим, якщо відношення довжин його сторін дорівнює .

Теорема. Якщо від золотого прямокутника відрізати квадрат, то прямокутник, який залишиться, також буде прямокутним.

B E C Нехай ABCD – золотий прямокутник,

ABEF – золотий квадрат. Позначимо

сторону квадрата через а.

АВ = ВЕ = а, ВС = а,

A F D ЕС = а – а = а ( - 1).

Знайдемо відношення сторін прямокутника ECDF:

= = .

Пригадаємо, що є коренем рівняння х = 1 + 1/x, тому

= 1 + 1/ і = = .

Теорему доведено.

Існує ще одна цікава властивість золотого перерізу: відношення радіуса кола до сторони правильного десятикутника, вписаного в це коло, є золотим перерізом, тобто R₁₀ : a₁₀ = .

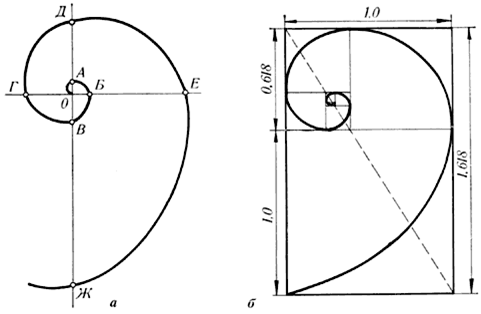
Рівнобедрений трикутник називають золотим, якщо відношення бічної сторони до основи цього трикутника дорівнює золотому перерізу.

Нагадаємо властивості золотого трикутника:

рівнобедрений трикутник із кутом 36⁰ при вершині є золотим;
бісектриса кута при основі золотого трикутника поділяє його на два трикутники, один з яких є золотим, а саме той, що прилягає до основи даного трикутника.

Золоті трикутники з’являються й при вивченні властивостей правильних многокутників: відношення довжини діагоналі правильного п’ятикутника до довжини його сторони дорівнює золотому перерізу. Ламана, яку утворюють діагоналі правильного п’ятикутника, буде зіркою. Ця зірка має таку чудову властивість: довільний відрізок цієї фігури знаходиться у відношеннізолотого перерізу до найменшого сусіднього відрізка.

Мабуть тому Піфагор вважав правильний п’ятикутник незвичайною фігурою і дарував його зображення тільки друзям як символ дружби. П’ятикутну зірку піфагорійці сприймали як символ здоров’я, саме її взяли символом свого союзу.

На перший погляд золотий переріз відрізка видається дуже складним і рідкісним. Але це не так, оскільки він існує у природі, а уважні люди його помітили.

Золотий переріз у природі

Золотий переріз був відомий і до Піфагора, ще в стародавньому Вавилоні. Таке правило поділу вигадали не люди, а створила сама природа.

Природа – справжній знавець геометрії.

У біологічних дослідженнях було показано, що, починаючи з вірусів і рослин і кінчаючи організмом людини, всюди виявляється золота пропорція, що характеризує відповідність і гармонійність їх будови. Золотий перетин визнано універсальним законом живих систем.

Було встановлено, що числовий ряд чисел Фібоначчі характеризує структурну організацію багатьох живих систем. Наприклад, гвинтове листорозміщення на гілці становить дріб (число оборотів на стеблі/число листів в циклі, напр. 2/5; 3/8; 5/13), відповідає рядамФібоначчі.

Добре відома «золота» пропорція п’ятипелюсткових квіток яблуні, груші та багатьох інших рослин. Носії генетичного коду – молекулиДНК і РНК – маютьструктуру подвійної спіралі; її розміри майже повністю відповідають чисел ряду Фібоначчі.

Гете підкреслював тенденцію до природи спіральності.

Павук плете павутиння спіралеподібно. Спіраллю закручується ураган. Перелякане стадо північних оленів розбігається по спіралі.

Гете називав спіраль «кривою життя». Спіраль побачили в розташуванні насіння соняшнику, в шишках сосни, ананасах, кактусах і т.д.

$C:\Documents and Settings\Администратор\Рабочий стол\ИТ\15.jpg$ $C:\Documents and Settings\Администратор\Рабочий стол\ИТ\16.jpg$ $C:\Documents and Settings\Администратор\Рабочий стол\ИТ\17.jpg$

Квітки і насіння соняшника, ромашки, лусочки у плодах ананаса, хвойних шишках «упаковані» за логарифмічними («золотими») спіралями, що завиваються назустріч одна одній, причому числа «правих» і «лівих» спіралей завжди ставляться один до одного, як сусідні числа Фібоначчі.

Розглянемо стебло цикорію. Від основного стебла утворився відросток. Тут же розташувався перший листок. Відросток робить сильний викид в простір, зупиняється, випускає листок, але вже коротше першого, знову робить викид в простір, але вже меншої сили, випускає листок ще меншого розміру і знову викид.

$C:\Documents and Settings\Администратор\Рабочий стол\ИТ\18.gif$

Якщо перший викид прийняти за 100 одиниць, то другий дорівнює 62 одиниці, третій – 38, четвертий – 24і т.д. Довжина пелюсток теж підпорядкована золотій пропорції. У зростанні, завоюванні простору рослина зберегла певні пропорції. Імпульси її зростання поступово зменшувалися в пропорції золотого перерізу.

У багатьох метеликів співвідношення розмірів грудної і черевної частини тіла відповідає золотій пропорції. Склавши крила, нічний метелик утворює правильний рівносторонній трикутник. Але варто розвести крила, і ви побачите той же принцип членування тіла на 2,3,5,8. Бабка також створена за законами золотої пропорції: відношення довжин хвоста і корпусу дорівнює відношенню загальної довжини до довжини хвоста.

$C:\Documents and Settings\Администратор\Рабочий стол\ИТ\19.jpg$ $C:\Documents and Settings\Администратор\Рабочий стол\ИТ\20.jpg$

Людина – вінецьтворіння природи... Встановлено, що золоте співвідношення можна знайти і в пропорціях людського тіла.

У 1855 р. німецький дослідник золотого перерізу професор Цейзинг опублікував свою працю «Естетичні дослідження».

Цейзинг виміряв близько двох тисяч людських тіл і прийшов до висновку, що золотий перетин виражає середній статистичний закон.

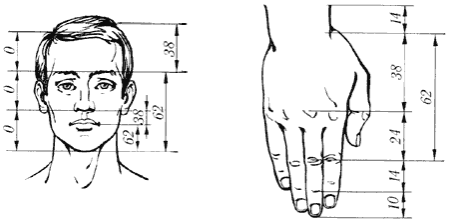
$C:\Documents and Settings\Администратор\Рабочий стол\04.gif$

Поділ тіла точкою пупа – найважливішийпоказник золотого перерізу. Пропорції чоловічого тіла коливаються в межах середнього відношення 13 : 8 = 1,625 і трохи ближче підходять до золотого перерізу, ніж пропорції жіночого тіла, відносно якого середнє значення пропорції виражається в співвідношенні 8 : 5 = 1,6.

У новонародженого пропорція становить відношення 1 : 1, до 13 років вона дорівнює 1,6, а до 21 року дорівнює чоловічий.

Пропорції золотого перетину виявляються і щодо інших частин тіла – довжинаплеча, передпліччя і кисті, кисті і пальців і т.д.

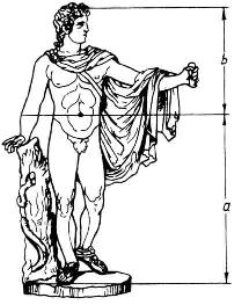
Справедливість своєї теорії Цейзинг перевіряв на грецьких статуях. Найбільш детально він дослідив пропорції Аполлона Бельведерського.

Описание: http://rudocs.exdat.com/pars_docs/tw_refs/174/173167/173167_html_7f874f0b.jpg

Піддалися дослідженню грецькі вази, архітектурні споруди різних епох, рослини, тварини, пташині яйця, музичні тони, віршовані розміри.

Цейзинг дав визначення золотого перерізу, показав, як воно виражається у відрізках прямої та в цифрах. Коли цифри, що виражають довжини відрізків, були отримані, Цейзинг побачив, що вони складають ряд Фібоначчі.

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 і т.д. відомий як ряд Фібоначчі. Особливість послідовності чисел полягає в тому, що кожен її член, починаючи з третього, дорівнює сумі двох попередніх 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 і т.д., а ставлення суміжних чисел ряду наближається до відношенню золотого перерізу.

Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. (або 1.618, якщо ділити більшого числа на менше).

Ряд Фібоначчі міг би залишитися тільки математичним казусом, якби не та обставина, що всі дослідники золотого поділу в рослинному і тваринному світі, не кажучи вже про мистецтво, незмінно приходили до цього ряду як арифметичного виразу закону золотого перерізу.

Золотий переріз у мистецтві, архітектурі, скульптурі.

Німецький фізик і психолог Густав Фехнер, один із основоположників експериментальної психології, дослідив, що людині подобається більше той прямокутник, сторони якого знаходяться у відношенні золотого перерізу. Тому нам більше подобаються і здаються прекрасними ті речі, що відповідають золотому перерізу.

Золотий переріз широко використовується в теорії і практиці скульптури, живописі, архітектурі. Пропорційність означає додержання певних співвідношень між окремими частинами споруди, картини, скульптурного твору, що справляє найприємніше враження. Архітектуру часто називають «замерлою музикою».

Описание: http://rudocs.exdat.com/pars_docs/tw_refs/174/173167/173167_html_7d2fc04b.jpg

«Золотий переріз» в конструкції Парфенону, Афіни, Греція

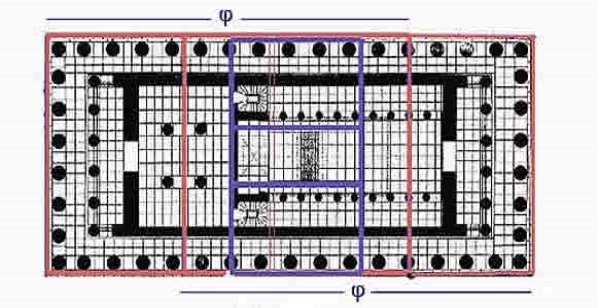
Описание: http://rudocs.exdat.com/pars_docs/tw_refs/174/173167/173167_html_3673fa22.jpg

План підлоги Парфенону

Німецький письменник Новаліс сказав: «У музиці чимало подібного алгебрі». Учення про відношення та пропорції стародавні греки називали музикою, яку вважали галуззю математики. Вони знали, що чим слабше натягнуто струну, тим нижчий («товщий», «грубіший») звук вона дає, а чим тугіше натягнуто струну, тим звук вищий. Але в музичному інструменті не одна, а кілька струн. Щоб усі вони під час гри звучали узгоджено, їх довжини повинні перебувати в певному відношенні. Тому вчення про відношення та пропорції і називалось у греків музикою.

Прославлені італійські майстри скрипкових інструментів Н. Аматі (1596 – 1684) і А. Страдіварі (1644 – 1737) свідомо використовували пропорцію золотого перерізу. Хоча ми не маємо інформації про те, як впливає застосування золотого перерізу при зовнішньому оформленні скрипки, на якість звуку, але безперечним є те, що це не перешкодило скрипковим інструментам, створеним знаменитими італійськими майстрами, стати і залишитися до нашого часу найкращими у світі. (Уся подальша інформація повідомляється під супровід тихої класичної музики).

Cередньовічнийченець і математик Лука Пачіолі у 1509 році написав трактат «Про божественну пропорцію». Автор вважає, що золотому перерізу притаманні чудові властивості. Він був переконаний, що пропорція існує скрізь: у географії, математиці, механіці, медицині та інших науках. А ілюстрації до цієї книги виконав Леонардо да Вінчі (1452 – 1519).

За словами російського літературознавця О. Дживелегова живопис приходив до математики через учення про перспективу і через оптику, скульптура через учення про пропорції, архітектура – через учення про масу й вагу тіл і – через те ж учення про пропорції. Мистецтво ставало наукою. Ніхто не відчував цього так ясно і міцно, як Леонардо да Вінчі, і недарма в його творчості мистецтво й наука стали двома сторонами одного й того самого, чимось неподільним.

Видатний художник, інженер та астроном епохи Відродження Леонардо да Вінчі на одному зі своїх малюнків зобразив людину у центрі Всесвіту, демонструючи, як використовується математика, а саме золотий переріз, для зображення ідеальних пропорцій людського тіла.

Описание: http://rudocs.exdat.com/pars_docs/tw_refs/174/173167/173167_html_936bbc0.png

Розглянемо портрет Мони Лізи. Його композиція базується на золотих трикутниках, що є частинами правильного зіркового п’ятикутника, та золотих прямокутниках.

Описание: http://rudocs.exdat.com/pars_docs/tw_refs/174/173167/173167_html_64b748e7.jpg

Золотий переріз широко використовували в архітектурі. Тільки дотримуючись законів геометрії, архітектори змогли створити свої шедеври. Пропорція в архітектурі – це ніби її внутрішня краса. Вона невидима безпосередньо,але завжди відчутна, як і краса духовна. Розглянемо фасад одного з найкращих витворів давногрецьких архітекторів – храм богині Афіни у Парфеноні, побудований у V ст. до н. е., залишки якого збереглися до наших днів. У розмірах окремих архітектурних деталей витримано пропорції золотого перерізу, а саме відношення висоти цієї будівлі до її довжини.

Архітектором ФіліппоБрунеллескі у XV ст. на основі золотого перерізу створена капела Пацці у Флоренції. Золотий переріз використано під час побудови багатьох споруд з колонами, фрагментів архітектури у Києві, Санкт – Петербурзі, Москві, Римі архітекторами В.В. Растреллі, К.І. Россі, А.Н. Вороніхіним тощо.

Золотий переріз та складання паркетів

В античній науці була широко відома «проблема паркету». Складання паркетів – це покриття площини фігурами одного чи кількох видів, що правильно чергуються.

Прикладом найпростіших паркетів може бути звичайний папір у клітинку або площина, заповнена однаковими правильними трикутниками. Будувати паркети можна із правильних многокутників з різною кількістю сторін. Для дослідження цього питання необхідно врахувати можливі типи «вузлових» точок, тобто знайти різні комбінації правильних многокутників, що можуть сходитися своїми вершинами в одній точці, заповнюючи без взаємних перекриттів її окіл, і в кожному випадку перевіряти можливість необмеженого продовження паркету з вузловими точками знайденого типу ([21]). Легко переконатися, що таке заповнення можна зробити за допомогою трикутників, квадратів, шестикутників, а за допомогою п’ятикутників (пентагонів) таке заповнення неможливе.

Звіт третьої творчої групи

Девіз: «Величність людини – у її вмінні мислити» (Б. Паскаль).

Захист проекту «А знання з геометрії виявляються корисні!»

Мета нашого дослідження – показати застосування подібності трикутників під час вимірювання висот, довжин об’єктів, що є недоступними.

Не перепливаючи річки, виміряти її ширину – так само просто для того, хто знає геометрію, як і визначити висоту дерева, не піднімаючись на його вершину. Неприступну відстань вимірюють тими ж прийомами, якими вимірюють неприступну висоту. В обох випадках обчислення невідомої відстані замінюється проміром іншої відстані, що легко піддається безпосередньому виміру. Для цього використовують відомі співвідношення у геометричних фігурах, ознаки рівності трикутників, ознаки подібності трикутників, які базуються на узагальненій теоремі Фалеса.

Презентація учасників проекту:

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Давньогрецький учений Фалес Мілетський (-625 – 547 рр. до н. е.) першим висунув і застосував ідею доведення в геометрії. Про це розповідають математики, які жили після нього. Геродот розповідав, що Фалес провіщав сонячне затемнення (585 р. до н. е.). Памфіла, письменниця епохи Нерона (римського імператора І ст.), за словами Діогена, говорила, що Фалес першим описав коло навколо прямокутного трикутника. Він довів, що вертикальні кути рівні, будь – яка хорда менша за діаметр, діаметр ділить круг навпіл, кути при основі рівнобедреного трикутника рівні, вписаний кут, що спирається на діаметр, прямий. І, зрозуміло,він першим довів теорему, яка з того часу названа його ім’ям. Не випадково в Греції Фалеса вважали одним із семи мудреців світу і склали про нього чимало легенд. Деякі з них дійшли до нас. Ось які історії про Фалеса Мілетського розповідає Г. Б. Філіпповський у книзі «Авторська шкільна геометрія».

N Історія 1 розповідає про те, як

_ - _ _ - - - _ _- - _ _ --- _ юнак Фалес допомагав захищати рідний

_ _ _ _ _ _ __ -- _- --__ Мілет від кораблів ворога.

_ - _ __---_ _ - ___----_ _ Уявимо, що дивимося на події з

_ ---__-_-__--__ ----_____ висоти пташиного польоту. Захисники

фортеці з катапульти К намагаються

влучити в корабель N (рис. 1). Але вода

K «скрадає» відстань, і жодний камінь не

Рис. 1 долітає в ціль.

Зараз я точно підрахую відстань до корабля! – упевнено заявляє

друзям Фалес. Вони недовірливо посміхаються, а дехто навіть крутить пальцем біля скроні: ти що, друже, збожеволів? Але Фалес цього не бачить, оскільки вже робить виміри. Він проходить уздовж передньої лінії деяку відстань КС (рис. 2 ) і в точці С вбиває в землю кілочок на висоту свого зросту. Потім проходить ще таку саму відстань: CD = KC і, повернувшись на 90⁰, іде у середину фортеці. Тільки-но в деякій точці Т його око сполучає верх кілочка й центральну щоглу корабля. Фалес кричить: «Я обчислив! Відстань до корабля знайдено!».

N Справді, за катетом KC =

DC і гострим кутом . Отже,

TD = NK. Таким чином, обчисливши TD,

можна точно визначити оптимальне

бойове положення катапульти і захистити

D C K від ворогів рідне місто.

Рис. 2

Історія 2 про те, як, мандруючи Єгиптом, Фалес був уражений величчю піраміди Хеопса.

Скажіть, будь ласка, яка висота піраміди? – запитав він жерців.
Про це дано знати хіба що богу Сонця Ра, а не людині, − відповіли жерці.
Хвилиночку, зараз я точно обчислю висоту піраміди! – запевнив їх Фалес.

J С

A T К

Рис. 3

Він вийшов на сонце й виміряв довжину своєї тіні. Тінь виявилася вдвічі більшою за зріст Фалеса, з чого він зробив висновок, що в цей момент усі предмети мають тінь удвічі більшу, ніж самі предмети. Залишається обчислити довжину тіні піраміди Хеопса. Вона дорівнює ОК, або ON + NK, або TD + NK (рис. 3). Відстані TD = AD i NK виміряти неважко. Знаходимо OK = TD + NK. Висота піраміди SO = OK.

Ви думаєте, жерці були вражені розумом і винахідливістю Фалеса? Зовсім ні. Вони страшенно обурилися. Ще б пак! Те, що взагалі не дано познати людині, якийсь там грек з Мілета обчислив майже миттєво!.. Таке не пробачають! І єгипетські жерці вирішили вбити Фалеса. На щастя, один з них виявився порядною людиною й порадив Фалесу швидше сідати на корабель, що от – от відпливав з Єгипту.

Фалес виміряв висоту об’єкту за допомогою тіні, а герой із твору Ж. Верна «Таємничий острів» Сайрес Сміт за допомогою жердини ([13]). Своїми знаннями з геометрії він зумів визначити координати острова, де вони опинилися, і тим самим врятував життя своїм друзям.

Сайрес Сміт взяв із собою пряму рівну жердину довжиною біля двадцяти футів – довжину він визначив за власним зростом, який він знав абсолютно точно. ГербертуСайрес Сміт доручив нести висок, тобто гнучку ліану, до кінця якої був привішений звичайний камінь.

Зупинившись приблизно кроках у двадцяти від узбережжя і кроках у п’ятистах від гранітного кряжу, Сайрес Сміт устромив жердину в пісок і старанно випрямив її, добившись шляхом вивірки виском, щоб вона стояла перпендикулярно до площини обрію.

Зробивши це, Сайрес Сміт відійшов і ліг на землю на такій відстані, щоб у полі його зору знаходився і верхній кінець жердини, і гребінь гранітної стіни. Це місце він позначив на піску кілочком і, коли повернувся до Герберта, спитав:

Ти знайомий з геометрією?
Трохи, містер Сайрес, − відповів Герберт, остерігаючись ускочитив халепу.
Пам’ятаєш властивості подібних трикутників?
Так, − відповів юнак, − у подібних трикутників відповідні сторони пропорційні одна одній.

D − Так от, дитя моє, у мене тут два

подібних прямокутних трикутники, −

B один менший, у ньому двома сторонами

будуть жердина, встромлена

перпендикулярно в пісок, і пряма, що

K A C дорівнює відстані від нижнього кінця

Рис. 4 жердини до кілка, а гіпотенузою − мій

промінь зору; у другого трикутника

сторонами будуть стрімка лінія гранітної стіни,висоту якої нам треба виміряти, відстань від кілка до підніжжя стіни, а в якості гіпотенузи – мій промінь зору, тобто продовження гіпотенузи першого трикутника.

Зрозумів, містере Сайрес! Я все зрозумів! – викликнув Герберт. –

Відстань від кілка до жердини пропорційна відстані від кілка до підніжжя стіни, а висота жердини пропорційна висоті стіни.

Правильно, Герберте, − підтвердив інженер. – І коли ми виміряємо

обидві відстані від кілка, то, знаючи висоту жердини, ми швидко розв’яжемо пропорцію і таким способом визначимо висоту стіни, що позбавить нас від мороки вимірювати її безпосередньо.

Виміряти висоту об’єкта можна різними способами: за допомогою великого пальця руки, записника і олівця, лінійки. У 7 класі на уроках фізики ви вивчали закони відбивання світла та використовували їх для побудови зображення в дзеркалі. Знайти висоту об’єкта можна за допомогою дзеркала. Існують також засоби вимірювання недосяжних відстаней, що застосовуються людьми на практиці, на перший погляд, зовсім не раціональні і не зрозумілі. Наприклад, вимір відстані «за допомогою козирка». Ось як цей спосіб знадобився старшому сержантові Куприянову у фронтових обставинах (Демидов А. «Розвідка ріки») ([13]). Його відділенню було наказано виміряти ширину річки, через яку необхідно було організувати переправу.

Коли відділення Куприянова підібралось до кущів біля річки і воїни залягли, сам Куприянов разом з солдатом Карповим підібралися ближче до річки, звідки добре було видно зайнятий фашистами берег. У таких умовах вимірювати ширину річки необхідно було на око.

Ну як, Карпов, скільки? – спитав Куприянов.
Як на мене, то не більш ніж 100 – 110 метрів, − відповів Карпов.

Куприянов був згодний зі своїм розвідником, але для контролювирішив виміряти ширину річки за допомогою «козирка».

Для цього необхідно стати лицем до річки і насунути кашкет на очі так, щоб нижня частина козирка точно співпала з лінією протилежного узбережжя. Козирокможна замінити долонею руки або записником, щільно притиснувши ребром до лоба. Потім, не змінюючи положення голови, повернутися праворуч чи ліворуч або навіть назад (у той бік, де більш рівна поверхня землі, що є доступною для виміру відстані) і примітити точку, яка є найдальшою видимою з – під козирка.

Відстань до пішохода, який іде іншим берегом річки, можна визначити за допомогою великого пальця руки, використовуючи подібність трикутників, знаючи відстань між очима.

Отже, деколи знання ознак і властивостей подібності трикутників допомагає і в екстремальних ситуаціях. Існують прилади, розроблені людьми, що допомагають одразу визначити висоту дерева, стовпа чи будівлі або необхідну відстань. Це – висотомір і далекомір.([13])

Ми також спробували скористатися знаннями з геометрії.

Висновок по 8-му класу

Під час виконання проекту учнями 8-го класу було досягнуто основної мети – дана відповідь на питання: «Чи варто вчити геометрію?». В процесі проектування виконано: 1) освітню функцію – сформовано в учнів систему спеціальних знань, умінь та навичок на різних етапах навчання; 2) розвиваючу функцію – вміння осмислити зміст понять, застосовувати здобуті знання на практиці; 3) виховну функцію – сформовано компетентності учнів.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Кулінка Юлія Cергіївна

Пов’язані теми

Геометрія, 8 клас, Матеріали до уроків

Додано

11 січня 2018

Переглядів

7552

Оцінка розробки

Відгуки відсутні