Геометрія

7   клас

Урок 50.  Тема: Контрольна робота №4 з теми «Сума кутів трикутника. Прямокутний трикутник»

 Очікувані результати перевірити рівень знань учнів, передбачений програмою з цього тематичного блоку, і вміння застосовувати отримані знання під час розв'язування задач.  

Хід уроку I.        Виконайте контрольну роботу

Варіант 1

Початковий рівень

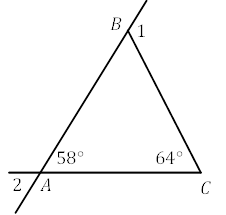
Б) ∆𝐴𝐵𝐶 –

прямокутний;

Г) ∠2 – зовнішній кут

∆𝐴𝐵𝐶

А) 73°                     Б) 90°                              2. (1 б) У трикутнику один з

кутів дорівнює 73°. Якою не

В) 107°                                                              Г) 110°        може бути градусна міра іншого кута?

            Середній рівень 3. (1 б) У прямокутному трикутнику 𝐾𝐿𝑁, кут 𝐿 – прямий, ∠𝐾 = 77°. Розташуйте в порядку зростання довжини відрізків 𝐾𝑁, 𝐿𝑁, 𝐾𝐿.

4. 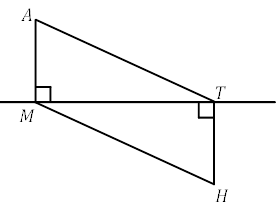    (2 б) Доведіть, що якщо на рисунку 𝐴𝑀 і 𝐻𝑇 перпендикулярні до прямої 𝑀𝑇 і 𝐴𝑇 = 𝐻𝑀, то ∆𝐴𝑀𝑇 = ∆𝐻𝑇𝑀

Достатній рівень

5.     (1 б) У прямокутному трикутнику 𝐾𝐿𝑁 з прямим кутом 𝐿 і ∠𝑁 = 37° проведена висота 𝐿𝐻. Знайдіть ∠𝐾𝐿𝐻

6.     (2 б) Кути трикутника відносяться як 1: 6: 8. Знайдіть кут 𝐴, якщо 𝐵𝐶 найменша сторона.

Високий рівень

7.     (1 б) У рівнобедреному трикутнику кут при основі дорівнює 14°. Знайдіть зовнішній кут при вершині цього трикутника.

8.     (2 б) У прямокутному трикутнику 𝑀𝑁𝑉 (кут 𝑀 – прямий) на гіпотенузі взяли точку 𝐾 так, що 𝑁𝐾 = 𝐾𝑀. Доведіть, що 𝑁𝐾 = 𝐾𝑉.

Варіант 2

Початковий рівень

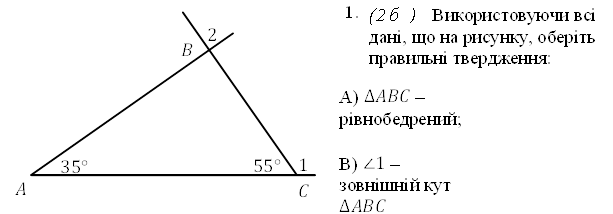
               1. (2 б) Використовуючи всі дані, що на рисунку, оберіть правильні твердження:

А) ∆𝐴𝐵𝐶 – Б) ∆𝐴𝐵𝐶 – рівнобедрений; прямокутний;

                                                                                                           В) ∠1 –                   Г) ∠2 –

                                                                                                           зовнішній кут         зовнішній кут

                                                                                                           ∆𝐴𝐵𝐶                      ∆𝐴𝐵𝐶

^{А) 90°                   Б) 138}                          2. (1 б) У трикутнику один з кутів

                                                 Г) Градусна міра              дорівнює 43°. Якою не може

В) 86°                   іншого кута може               бути градусна міра іншого кута?

бути будь-якою

Середній рівень 3.(1 б) У прямокутному трикутнику 𝑅𝑆𝑇, кут 𝑆 – прямий, ∠𝑅 = 42°. Розташуйте в порядку зростання довжини відрізків 𝑅𝑇, 𝑆𝑇, 𝑅𝑆.

4. 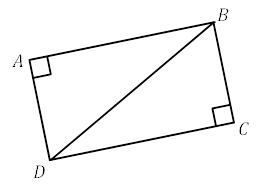    (2 б) Доведіть, що якщо на рисунку ∠𝐴 і ∠𝐶 прямі і 𝐷𝐶 = 𝐴𝐵, то

∆𝐷𝐴𝐵 = ∆𝐵𝐶𝐷

Достатній рівень

5.     (1 б) У прямокутному трикутнику

𝑀𝑁𝑉 з прямим кутом 𝑁 і ∠𝑀 = 48° побудована висота 𝑁𝐻.

Знайдіть ∠𝐻𝑁𝑉.

6.     (2 б) Кути трикутника відносяться

як 3: 4: 5. Знайдіть кут 𝑉, якщо 𝑀𝑁 найбільша сторона.

Високий рівень 7.(1 б) У рівнобедреному трикутнику кут при основі дорівнює 18°. Знайдіть зовнішній кут при вершині цього трикутника.

8.(2 б) У прямокутному трикутнику 𝐾𝐿𝑁 (кут 𝐿 – прямий) на гіпотенузі взяли точку 𝑆 так, що ∠𝑆𝐾𝐿 = ∠𝐾𝐿𝑆. Доведіть, що 𝑆𝐿 = 𝑆𝑁

II.     Домашнє завдання

Повторити §17-20