КОНТРОЛЬНА РОБОТА З МАТЕМАТИКИ  ЗА ПЕРШИЙ СЕМЕСТР

(6 КЛАС, ТАРАСЕНКОВА Н.А.)

ВАРІАНТ 1

Початковий і середній рівень (5б)

Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.

 

1.   У коробці 7 жовтих і 14 червоних олівці. Яка ймовірність навмання витягнути з коробки жовтий олівець?

 

А) 67%;            Б) 33% ;  В)  50%;   Г) 30%;

 

2.   Чому дорівнює АО, якщо площа основи конуса дорівнює 200,96 см?

 

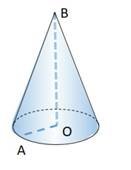
А) 25,12 см    Б) 8 см     В) 50,24 см   Г) 16 см

 

3.   Прочитай діаграму. Яка тварина живе довше? Скільки живе у середньому мавпа, собака, крокодил?

 

 

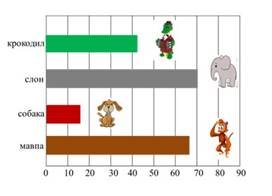
А) слон - 80 р, мавпа - 70 р, собака - 42 р, крокодил –15 р

Б) слон - 70 р, мавпа - 15 р, собака - 17 р, крокодил – 50р            

В) слон - 70 р, мавпа - 65 р, собака - 15 р, крокодил – 42 р

Г) слон - 70 р, мавпа - 65 р, собака - 25 р, крокодил – 30 р

 

4.   Вам треба пофарбувати круг радіусом 3 м. Витрати фарби на 1 м складають 120 г. Скількі потрібно для цього купити банок фарби, якщо у банці її 1 кг?

 

А) 4    Б) 5     В) 3   Г)  5. Скоротіть дроби:

                                                                       ,     ,     ,     .

 

Достатній рівень (4б)

Розв’язання завдань  6 – 7  повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.

6.   Виконайте дії:

4 8 ₋11_17 .

_

                                                                                  15      3   8

7.   Розв’яжіть рівняння

                                                                          −9 3+5 8 = 6 5 .

х

                                                                                7      21      14

 

Високий рівень (3б)

Розв’язання  завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу.  Завдання оцінюється трьома балами.

 

8.  За три тижні  було відремонтовано  108 км  дороги. За перший тиждень було відремонтовано    дороги,  а за другий  –   решти. Скільки кілометрів  дороги відремонтували за третій тиждень?

 

 

 

 

 

 

 

 

 

 

 

КОНТРОЛЬНА РОБОТА З МАТЕМАТИКИ  ЗА ПЕРШИЙ СЕМЕСТР

(6 КЛАС, ТАРАСЕНКОВА Н.А.)

ВАРІАНТ 2

Початковий і середній рівень (5б)

Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.

 

1.   У скрині лежать 6 білих хустинок, 3 червоні й одна зелена. Яка імовірність витягнути зі скрині білу хустину?.

А) 50%;            Б)  40%;              В)  60%;     Г) 33%;

 

2.   Яка площа бокової поверхні циліндру, якщо його радіус ОА=5 см і висота ОО₁=5 см?

 

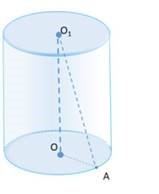
А) 157 см2        Б) 78,5 см2          В) 25 см2       Г) 392,5 см2

 

3.   Використовуючи подану діаграму, встановить скількі хвилин школяр витрачає на компьютерні ігри. Результат округліть до цілої частини.

 

 

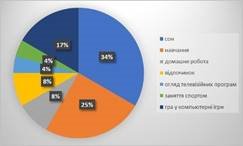
А) 150 хв                   Б) 180 хв           В) 240 хв                         Г) 240 хв

 

 

 

4.   Довжина кола арени дорівнює 42 м. (Пі= 3). Знайдіть площу арени

 

А) 63 м2      Б) 147 м2   В) 49 м2     Г) 150 м2

 

                                                                 

5.   Скоротіть дроби:    

                                                                        ,    ,    ,     .

Достатній рівень (4б)

Розв’язання завдань  6 – 7  повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.

6.   Виконайте дії:

2 2 +15:11 .

                                                                                    3      6    2

7.   Розв’яжіть рівняння: х −27_+35 ₌ 4 2 .

                                                                                          8      6       3

 

Високий рівень (3б)

Розв’язання  завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу.  Завдання оцінюється трьома балами.

 

8.  За три дні  було прокладено  112 м  дроту. За перший день  проклали    дроту, а  за другий  –   решти. Скільки метрів  дроту проклали за

третій день?