Контрольні роботи з алгебри для 7 класу.

 

 

 

 

Передмова

 

    Пропонований посібник містить завдання для тематичних контрольних робіт у 4 варіантах.

  

 Завдання, позначені «○», відповідають початковому

та середньому рівням, «●» - достатньому, а «●●» - високому рівням навчальних досягнень.

  

 Тематика робіт та їх зміст відповідають чинній програмі Міністерства освіти і науки України й орієнтовані на підручник «Алгебра, 7 клас»

(автори Г. Бевз, В. Бевз), однак запропоновані завдання можна використовувати і під час роботи

з іншими підручниками.

 

  Кількість завдань і час необхідний для виконання контрольних робіт, учитель вибирає самостійно, враховуючи психолого-педагогічну характеристику класу й індивідуальні особливості учнівського колективу.

 

  Контрольна робота розрахована на один урок.

 

 

 

 

 

 

 

Контрольна робота №1

 

Лінійні  рівняння з однією змінною

 

 

I варіант

 

 

1) Яке з чисел є коренем рівняння -0,2х=3?

 

 

А) 3,2;              Б) 2,8;         В)-15;          Г)-6.

 

 

2)Розв’язати рівняння:

 

           

             А) х + 25 = 49;           Б)2х-(6х-5)=45;          В) 5х – 1,7 = 3,7 – 4х..

 

 

3) Розв’язати задачі:

 

 

А) На двох полицях 146 книжок, причому на другій – на 12 книжок більше, ніж на першій. Скільки книжок на кожній полиці?

 

 

Б) У трьох класах 86 учнів. У першому класі на 1 учня менше, ніж у другому ,а в третьому –на 3 учні менше, ніж у другому. Скільки учнів у кожному класі ?

 

 

4 )Спростити  рівняння  і  знайти його корені :

 

 

А)   +х = 0,5х – 3;               Б)-=.

 

 

 

 

II варіант 

             

 

1)Яке з чисел є коренем рівняння  5 х = -3?

 

                    А)-15;            Б)-;             В)-;            Г)-8.

 

 

2)   Розв’язати рівняння:

 

          

А)х +28 = 49;             Б)8у-(4у+5)=35;                В) 2х  – 3,7 = 2 ,7–2х.

      

 

3) Розв’язати задачі :

 

 

А) У двох бригадах працює 160 робітників, причому в першій у 3 рази більше, ніж у другій. Скільки робітників працює у кожній бригаді?

  

 

Б) У трьох мішках 114 кг зерна . У першому мішку зерна у 3 рази більше, ніж у другому, а в третьому – на 9 кг зерна більше , ніж у першому. Скільки зерна у кожному мішку?

 

 

4 )Спростити  рівняння  і  знайти його корені:

       

 

      А)    10 + = 14,2;             Б) -= .

 

 

 

 

 

 

 

 

 

 

III варіант               

 

 

1) Яке з чисел є коренем рівняння    4х+2=10?

 

 

А) 1;          Б) -2;          В) 2;         Г) 3.

 

 

2) Розв’язати рівняння:

 

 

           А) у + 14 = 51;        Б)5х –( 7х + 7) =9;         В)   5х – 4,5 = 3х +2,5.

  

 

3) Розв’язати задачі :

 

 

А)У двох зерносховищах 294 т зерна. Скільки зерна у кожному зерносховищі, якщо в першому в 5 раз  більше, ніж у другому?

 

 

Б)Три робітники  виготовили 67 деталей. Перший робітник виготовив на 7 деталей більше,  ніж другий, а третій робітник у 2 рази більше, ніж другий. Скільки деталей виготовив кожний робітник?

 

 

4 )Спростити рівняння  і  знайти його корені:

 

 

А) 10 +=1,2х +2;                      Б) =-.

 

 

 

 

 

 

 

 

 

IV варіант

 

 

1)Яке з чисел є коренем рівняння  3х – 5 = -8?

 

А)1;          Б)-1;          В);           Г).

 

2)Розв’язати рівняння:

  

 

     А) в +38 = 65;           Б)12с –( 10с-7 )=27;           В)6х -0,8 =3х +2,2.

 

 

3)Розв’язати задачі :

 

 

А)На двох полицях 163 книжки. Скільки книжок на кожній полиці, якщо на одній  з них на 17 більше, ніж на другій.

 

 

Б)За три дні робітник виготовив 66 деталей. За перший день він виготовив на 8 деталей менше, ніж за другий , і на 5  деталей більше, ніж за третій. Скільки деталей виготовляв робітник кожного дня?

 

 

4 )Спростити  рівняння  і  знайти його корені:

 

 

             А) 3-= х-1,5;                      Б) =-.  

 

 

 

 

 

 

 

 

 

 

 

Контрольна  робота № 2

 

Цілі вирази. Одночлени.

 

I варіант.

 

1) Обчислити:

 

А);         Б);         В).

 

2) Знайти значення виразу:

 

 

, якщо а=4; в=8.

 

3) Виконати дії:

 

 

А);       Б);         В)m: m;        Г) x: (x) x;      Д).

 

 

4) Подати у вигляді многочленна стандартного вигляду.

 

 

(-0,2 )(-1,5)

 

 

5) Спростити вирази :

 

 

А);        Б) ;      В) .

 

 

 

 

 

 

 

 

ІI варіант.

 

 

1) Обчислити:

 

А);         Б);        В).

 

 

2) Знайти значення виразу:

 

, якщо а=1; в=3.

 

 

3) Виконати дії:

 

А);        Б);           В) ;         Г);        Д).

 

 

4) Подати у вигляді многочленна стандартного вигляду.

 

 

 

 

5) Спростити вирази :

 

 

А);       Б) ;       В) .

 

 

 

 

 

 

 

 

 

 

 

ІІI варіант.

 

 

1) Обчислити:

 

А);         Б);        В).

 

 

2) Знайти значення виразу:

 

, якщо а=2; в=5.

 

 

3) Виконати дії:

 

А);     Б);      В) ;     Г);       Д).

 

 

4) Подати у вигляді многочленна стандартного вигляду.

 

 

 

 

5) Спростити вирази :

 

А);       Б);       В) .

 

 

 

 

 

 

 

 

 

 

 

IV варіант.

 

 

1) Обчислити:

 

А);      Б);    В).

 

 

2) Знайти значення виразу:

 

 

, якщо а=5; в=3.

 

 

3) Виконати дії:

 

А);        Б);        В) ;        Г);      Д) .

 

 

4) Подати у вигляді многочленна стандартного вигляду.

 

 

 

5) Спростити вирази :

 

 

А);         Б) ;       В) .

 

 

 

 

 

 

 

 

 

Контрольна  робота № 3

 

Многочлени

 

I варіант

 

1) Виконати дії:

А) (х + 2у ) + (2х +у) ;

 

Б) (4а +3в) – (7а + 2в);

 

В) 5х (3х – 7у);

 

Г) (а + в ) ( х – у ).

 

2) Записати многочлен у стандартному вигляді:

             

А) 5ху – 3у-2ху + 4у- ху;

 

Б) 3х ( х – 1) – 2х (х – 2).

 

3) Розв’язати рівняння:

              

А) х-14х -26 =х (х – 1);

 

Б)х (10х + 9) – (5х – 1)(2х + 3) = 8.

 

 4) Спростити вирази:

               

А) (5,2х  -1,3 + 4) 3 - 2,6х ( 6х-1,5);

           

Б) М N – R Q, якщо :

 

М = а-3,        N = а-8а +5,      R = а-8,       Q = а-3а+5.

 

 

II варіант

 

 1) Виконати дії:

 

А) (3х + у) + (3х +7у );

 

Б)(3а – 5в) – (7а + 5в);

 

В)2х (4х + 8у);

 

Г)(m – n) (а +с).

 

2) Записати многочлен у стандартному вигляді:   

                

А) 2ав – 7в- 5ав +3в+8ав;

 

Б) 2в (4а – 3в)-( в – 7а);

 

3) Розв’язати рівняння:

 

А) 3 – 4х + х= х (х – 2);

 

Б)4х ( х – 1) – ( 2х + 5) ( 2х – 3) =  9.

 

 4) Спростити вирази:

              

А) 2 (5,1х - 1,5х + 7) - 3х( 3х- х);

               

Б) АВ – СД , якщо

 

А = 2х- х 10;        В = х – 3;         С = х- 5х +4;        Д = 2х + 3.

 

 

 

IІI варіант

 

 1) Виконати дії:

               

А) (2m + 3n) + (3m +2n );

 

Б)(7x +2y) – (x + 3y);

 

В)2х (m + 3n - 2t);

 

Г)(a + m) (n -b).

 

2) Записати многочлен у стандартному вигляді:   

 

А) 3в + а+ 6ав - 10в+6ав;

 

Б) 2у (х – у) + у( 3у – 2х);

3) Розв’язати рівняння:

                 

А) х - 12х - 1= х (х – 2);

 

Б)(х - 2) ( х + 4) – ( х - 7) ( х + 5) =  3х.

 

 4) Спростити вирази:

               

А) (3,4х - 1,2х + 6) 3 - 4х( 2,55х – 0,9);

 

Б) АВ – СД , якщо

 

А = а+ 5 – 8а;       В = а – 3;       С = а - 8;    Д = 5 + а- 3а .

 

 

 

 

IV варіант

 

 1) Виконати дії:

 

А)(7x + 2y) + (2x + 7y);

 

Б)(5m – 3n) – (4m - 8n);

 

В)3a (6b + 4c);

 

Г)(a – b) (m +n).

2) Записати многочлен у стандартному вигляді:   

 

А);

 

Б) 2y (2x – 3y)+3y( 5y – 3x);

 

3) Розв’язати рівняння:

А) 3x –х- 7= х (4 - х);

 

Б)( 3 – 2x) – ( х + 7) = 3 + ( 4 - х) (2x+3).

 

4) Спростити вирази:

 

А) (4+x) (х- 4х + 16)- (х+4)(x – 4)x – 3,2( 5х- 2);

 

Б) MN – BС , якщо

 

M = x - 3;         N = 2х – x - 10;         B = 4+х- 5х;        C = 3+2х.

 

 

 

Контрольна робота №4

 

Розкладання многочленів на множники. Різниця квадратів.

Квадрат двочлена.

 

І варіант.

 

1) Винести спільний множник за дужки:

 

А) 15сb + 5bd;            Б) 6c – 12d + cx – 2 xd;      В) m(x – y).

 

2) Записати вираз у вигляді множника:

 

А) (a – 3);       Б)(2x + y) ;         В) (7 – x)(7 +x).

 

3) Записати тричлен у вигляді квадрата двочлена:

 

m- 12m + 36.

 

4) Розкласти на множники:

 

А) ;       Б) .

 

5) Спростити:

 

А) ;         Б) .

 

6) Обчислити найзручнішим способом:

 

 

7) Розв’язати рівняння:

.

 

 

 

ІІ варіант

 

1) Винести спільний множник за дужки:

 

А);         Б);       В) .

 

2) Записати вираз у вигляді множника:

 

А);        Б) ;          В).

3) Записати тричлен у вигляді квадрата двочлена

 

.

4) Розкласти на множники:

 

А) ;        Б) .

5) Спростити:

 

А) ;       Б) .

 

6) Обчислити найзручнішим способом:

 

7) Розв’язати рівняння:

 

.

 

 

 

 

 

 

ІІІ варіант

 

1) Винести спільний множник за дужки:

 

А);          Б);      В) .

 

2) Записати вираз у вигляді множника:

 

А);        Б) ;          В).

 

3) Записати тричлен у вигляді квадрата двочлена:

 

.

 

4) Розкласти на множники:

 

А) ;         Б) .

 

5) Спростити:

 

А) ;      Б) .

 

6) Обчислити найзручнішим способом:

 

 

7) Розв’язати рівняння:

 

.

 

 

 

 

 

 

 

ІV варіант

 

1) Винести спільний множник за дужки:

 

А);        Б);       В) .

 

2) Записати вираз у вигляді множника:

 

А);         Б) ;           В).

 

3) Записати тричлен у вигляді квадрата двочлена:

 

.

 

4) Розкласти на множники:

 

А) ;       Б) .

 

5) Спростити:

 

А) ;          Б) .

 

6) Обчислити найзручнішим способом:

 

 

7) Розв’язати рівняння:

 

.

 

 

 

 

Контрольна робота №5

Використання формул скороченого множення

І варіант.

 

1) Розкласти на множники многочлени:

 

А) 49 - a;          Б) + 27.

 

2) Розв’язати рівняння:

 

А) x- 10x = 0;        Б)(x - 7)=0 ;          В)  x- 10x + 25=0.

 

3) Обчислити значення виразу:

 

, якщо х=8.

 

4) Розкласти на множники многочлени:

 

А) ;         Б) ;         В)  .

 

5) Розв’язати рівняння:

 

А) ;          Б) .

 

6) Обчислити значення виразу:

 

 

 

 

IІ варіант.

 

1) Розкласти на множники многочлени:

 

А) x- 64;        Б) 8 - x.

 

2) Розв’язати рівняння:

 

 

А) 5x - x= 0;           Б)(x - 4)=0 ;          В)  x- 16x + 64=0.

 

3) Обчислити значення виразу:

 

, якщо х=4.

 

4) Розкласти на множники многочлени:

 

 

А) ;          Б) ;           В)  .

 

5) Розв’язати рівняння:

 

 

А) ;             Б) .

 

 

6) Обчислити значення виразу:

 

 

 

 

 

IIІ варіант.

1) Розкласти на множники многочлени:

 

А) 36 - m;              Б) x+64.

 

2) Розв’язати рівняння:

 

 

 

А) 9a - a= 0;              Б)(x - 5)=0 ;               В)  x+ 8x + 16=0.

 

3) Обчислити значення виразу:

 

, якщо a=10.

 

 

4) Розкласти на множники многочлени:

 

 

А) ;            Б) ;              В)  .

 

5) Розв’язати рівняння:

 

 

А ;              Б) .

 

6) Обчислити значення виразу:

 

 

 

 

 

ІV варіант.

 

1) Розкласти на множники многочлени:

 

А) 25 - a;        Б) m- 125.

 

2) Розв’язати рівняння:

 

 

А) y- 12y= 0;         Б)(m - 9)=0 ;            В)  a- 16a + 64=0.

 

3) Обчислити значення виразу:

 

 

, якщо х=8.

 

4) Розкласти на множники многочлени:

 

 

А) ;        Б) ;         В)  .

 

5) Розв’язати рівняння:

 

 

А) ;        Б) .

 

6) Обчислити значення виразу:

 

 

 

 

 

 

Контрольна  робота № 6

 

Функції.

 

I варіант.

 

 

1) Функцію  задано формулою  у = 2х + 4.

    

      Визначити :

 

      А) значення функції, якщо значення аргументу дорівнює 4;

 

      Б) значення аргументу, якщо значення функції дорівнює 10.

 

2) Функцію  задано формулою  у = . Яка з точок належить графіку цієї

       функції: А(-1;3); В(1;3); С(-2;-6); Д(-2;-8)?

 

 

3) Побудувати графік  функції у = 2х -1.

 

 

4) Знайти точки перетину графіка функції  у = -6х +18 з осями координат.

 

 

5) За якого значення  k графік прямої пропорційності у = kх проходить

       через точку М ( ;2).

 

 

6) Задати формулою лінійну функцію, графік якої проходить через початок координат і точку А(3;6).

 

 

7) Знайдти область визначення функції  у = .

 

8) Функцію задано f(x)=kx +b. Знайти k і в, якщо f(2)=5 і f()=9.

      Чи належить графіку функції точка К(7;-10)?

 

 

II варіант.

 

1) Функцію  задано формулою  у = 3х-2.

     

       Визначити :

     

       А) значення функції, якщо значення аргументу дорівнює 4;

        

       Б) значення аргументу, якщо значення функції дорівнює 10.

 

 

2) Функцію  задано формулою  у =- . Яка з точок належить графіку цієї

       функції: А(-1;3); В(1;3); С(-1;1); Д(-2;-8).

 

 

3) Побудувати графік  функції у = 3х -1.

 

 

4) Знайти точки перетину графіка функції  у =12х -24 з осями координат.

 

 

5) За якого значення  k графік прямої пропорційності у = kх проходить

       через точку М (;3).

 

6) Задати формулою лінійну функцію, графік якої проходить через початок координат і точку А(-2;-4).

 

 

7) Знайти область визначення функції  у = .

 

8) Функцію задано f(x)=kx +b. Знайти k і в, якщо f(4)=12 і f()= -5.

      Чи належить графіку функції точка F(-0,2;-9).

 

 

 

 

 

 

 

III варіант

 

1) Функцію  задано формулою  у = 2х-5.

 

      Визначити :

 

     А) значення функції, якщо значення аргументу дорівнює 4;

                

      Б) значення аргументу, якщо значення функції дорівнює 10.

 

2) Функцію  задано формулою  у =. Яка з точок належить графіку цієї

       функції: А(1;3); В(-1;4); С(2;4)); Д(-2-4).

 

 

 

3) Побудувати графік  функції у = 4х -1.

 

 

4) Знайти точки перетину графіка функції  у = -3х -15 з осями координат.

 

 

 

5) За якого значення  k графік прямої пропорційності у = kх проходить

       через точку М (;4).

 

6) Задати формулою лінійну функцію, графік якої проходить через початок координат і точку А(2;4).

 

 

7) Знайти область визначення функції  у = .

 

 

8) Функцію задано f(x)=kx +b. Знайти k і в, якщо f(3)=5 і f()= -3.

      Чи належить графіку функції точка F(-0,2;-9).

 

 

 

 

 

IV варіант

 

1) Функцію  задано формулою  у =4х+3.

 

        Визначити :

 

       А) значення функції, якщо значення аргументу дорівнює 4;

                 

       Б) значення аргументу, якщо значення функції дорівнює 10.

 

2) Функцію  задано формулою  у =-. Яка з точок належить графіку цієї

       функції: А(1;3); В(-1;-4); С(2;-4)); Д(-2;8).

 

 

3) Побудувати графік  функції у =5х-2.

 

 

4) Знайти точки перетину графіка функції  у =12х-36 з осями координат.

 

 

5) За якого значення  k графік прямої пропорційності у = kх проходить

      через точку М (;10)

 

6) Задати формулою лінійну функцію, графік якої проходить через початок координат і точку А(-3;-6).

 

 

7) Знайти область визначення функції  у = .

 

8) Функцію задано f(x)=kx +b. Знайти k і в, якщо f()=6  і f(5)=15.

      Чи належить графіку функції точка А(-7;-9).

 

 

 

 

 

 

 

 

Контрольна  робота № 7

 

Системи   лінійних  рівнянь

 

I варіант

 

1) Яка з пар чисел  є розв’язком  системи           

 

А)(2;0);       Б)(1;1);       В)(0;2);        Д)(-1;-1)?

 

 

2) Розв’язати графічно систему рівнянь:    

 

 

3) Розв’язати систему рівнянь способом підстановки:  

 

 

4) Розв’язати систему рівнянь способом додавання: 

 

 

5) Розв’язати задачу за допомогою системи рівнянь:

   

      За 2 кг груш та 3 кг яблук заплатили 20,5 грн. А за 2 кг яблук та 3 кг

     груш – 22 грн. Скільки коштує 1 кг яблук та 1 кг груш?

 

 

6)  Розв’язати систему рівнянь:  

 

 

 

 

 

 

 

 

II варіант

 

 

1) Яка з пар чисел  є розв’язком  системи   

 

 

А)(0;1);        Б)(-1;1);         В)(1;-1);        Г)(2;-2)?

 

 

2) Розв’язати графічно систему рівнянь:    

 

 

3) Розв’язати систему рівнянь способом підстановки:    

 

 

4) Розв’язати систему рівнянь способом додавання:

 

 

5) Розв’язати задачу за допомогою системи рівнянь:

   

     3 олівці  і 4 зошити коштують 2,2 грн.,а 5 олівців і 2 зошити – 1,8 грн.

     Скільки коштує  1 олівець і  1  зошит?

 

 

6)  Розв’язати систему рівнянь:

 

 

 

 

 

 

 

 

 

 

III варіант

 

 

1) Яка з пар чисел  є розв’язком  системи  

 

 

А)(1;2);       Б)(6;3);         В)(-6;3);        Г)(-1;-2)?

 

 

2) Розв’язати графічно систему рівнянь:   

   

 

3) Розв’язати систему рівнянь способом підстановки:    

 

 

4) Розв’язати систему рівнянь способом додавання: 

 

 

5) Розв’язати задачу за допомогою системи рівнянь:

    

     За 4 кг бананів та 3 кг апельсинів заплатили 35,5 грн.

     А за 2кг бананів та 2кг  апельсинів – 20 грн.

     Скільки коштує 1 кг бананів та й 1 кг апельсинів?

 

 

6)  Розв’язати систему рівнянь:

 

 

 

 

 

 

 

 

 

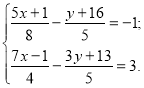
IV варіант

 

 

1)Яка з пар чисел  є розв’язком  системи  

 

 

А)(-4;3);       Б)(-1;-6);         В)(4;3);        Г)(1;6)?

 

 

 

2) Розв’язати графічно систему рівнянь:    

   

 

3) Розв’язати систему рівнянь способом підстановки:    

 

 

 

4) Розв’язати систему рівнянь способом додавання:

 

 

 

5) Розв’язати задачу за допомогою системи рівнянь:

    

      За 2 морозива і 3 батони заплатили 5,2 грн., а за  4 морозива і

      2 батони – 4,8 грн. Скільки коштує порція морозива і  1 батон?

 

6)  Розв’язати систему рівнянь:

 

 

 

 

 

 

 

 

Підсумкова контрольна  робота                    

 

I варіант

 

 

1) Виконати дії:

 

А);        Б);         В).

 

 

2) Розв’язати систему рівнянь:    

 

 

3) Розкласти на множники многочлени:

 

 

А);          Б);         В);        Г);

 

 

4) Розв’язати задачу:

 

     Турист пройшов 50 км за 3 дні. За другий день він пройшов на 10 км менше, ніж за перший і на 5 км більше, ніж за третій. Скільки кілометрів турист проходив щоденно?

 

 

5)  Розв’язати систему рівнянь:

 

 

 

 

 

 

 

 

 

 

 

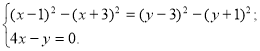
ІI варіант

 

 

1) Виконати дії:

 

А);      Б);      В).

 

 

2) Розв’язати систему рівнянь:    

 

 

 

3) Розкласти на множники многочлени:

 

 

А);         Б);       В);        Г);

 

 

 

4) Розв’язати задачу:

 

     Периметр трикутника АВС дорівнює 50 см. Сторона АВ на 2 см довша від сторони ВС, а сторона АС в 2 рази більша від сторони ВС. Знайти довжини сторін трикутника.

 

 

5)  Розв’язати систему рівнянь:

 

 

 

 

 

 

 

 

 

 

 

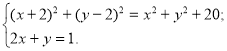
ІІI варіант

 

 

1) Виконати дії:

 

А);         Б);        В).

 

 

2) Розв’язати систему рівнянь:    

 

 

 

3) Розкласти на множники многочлени:

 

 

А);         Б); В);        Г);

 

 

4) Розв’язати задачу:

 

     Велосипедист їхав 2 год лісовою дорогою і 1 год по шосе, подолавши 40 км. При цьому його швидкість на шосе була на 4 км/год більша, ніж лісом. З якою швидкістю він їхав по шосе і з якою лісом?

 

 

5)  Розв’язати систему рівнянь:

 

 

 

 

 

 

 

 

 

 

 

 

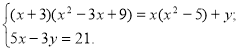
IV варіант

 

 

1)  Виконати дії:

 

А);         Б);       В).

 

 

2) Розв’язати систему рівнянь:    

 

 

3) Розкласти на множники многочлени:

 

 

А);           Б); В);         Г);

 

 

4) Розв’язати задачу:

 

     Відстань між пристанями А та В в обох напрямках катер пропливає за 8 год. Знайдіть цю відстань, якщо власна швидкість катера дорівнює 8 км/год, а швидкість течії – 2 км/год.

 

 

 

5)  Розв’язати систему рівнянь:

 

 

 

 

 

 

 

 

 

 

 

 

 

Для заміток                                                                                         1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для заміток                                                                                         1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зміст

 

1. Передмова                                                                                                   1

 

 

2. Контрольна робота №1 «Лінійні  рівняння з однією змінною»            2-5

 

 

3. Контрольна  робота № 2 «Цілі вирази. Одночлени»                                 6-9

 

 

4. Контрольна  робота № 3 «Многочлени»                                               10-13

 

5. Контрольна робота №4 «Розкладання многочленів на множники. Різниця квадратів. Квадрат двочлена»                                                     14-17

 

6. Контрольна робота №5 «Використання формул скороченого

множення»                                                                                                    18-21

 

 

7. Контрольна  робота № 6 «Функції»                                                      22-25

 

 

8. Контрольна  робота № 7 «Системи   лінійних  рівнянь»                    26-29

 

 

9. Підсумкова контрольна  робота                                                            30-33