Критичне мислення як провідна технологія в НУШ

Практичний посібник

2023

ЗМІСТ

ВСТУП……………………………………………………………………………….……….….……2

РОЗДІЛ 1. ТЕОРЕТИЧНІ ЗАСАДИ ФОРМУВАННЯ

КРИТИЧНОГО МИСЛЕННЯ ВУЧНІВ ПОЧАТКОВОЇ ШКОЛИ……………………………………………………………………….…………..……..4

1.1. Проблема формування критичного мислення

в учнів у науковій літературі……………………………………………...……….…….4

1.2. Розвиток критичного мислення як засіб

формування інтелектуальної культури дітей………………………………….…….6

РОЗДІЛ 2. МЕТОДИКА ФОРМУВАННЯ У ДІТЕЙ МОЛОДШОГО

ШКІЛЬНОГО ВІКУ КРИТИЧНОГО МИСЛЕННЯ………………………………….…….…...…..………………………………….7                                                 

2.1. Система роботи з формування критичного

мислення в учнів початкових класів на уроках………………………..….….…….7

2.2. Методичні рекомендації щодо формування

у дітей критичного мислення…………….………..….…….……….25

ВИСНОВКИ…………………………………………………………….……………………...…..27

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ…………………………….………..……………..28

ВСТУП

Постановка проблеми. Нова українська школа – це ключова реформа Міністерства освіти і науки. Головна мета – створити школу, у якій буде приємно навчатись і яка даватиме учням не тільки знання, а й вміння застосовувати їх у житті.

НУШ – це школа, до якої приємно ходити учням. Тут прислухаються до їхньої думки, вчать критично мислити, не боятись висловлювати власну думку та бути відповідальними громадянами[7].

Впродовж останніх років відомі вітчизняні вчені й педагоги у своїх працях все частіше звертаються до проблем реалізації компетентнісного підходу в навчальних закладах нашої держави. Так, у працях Т.Байбари, Н.Бібик, О.Заблоцької, Г.Кравченко, О.Савченко глибоко розглянуто теоретичні та практичні аспекти реалізації компетентнісного підходу в освіті загалом і в її початковій ланці зокрема [21, с.14].

Однак формування компетентної особистості неможливо уявити без розвитку в неї критичного мислення. Дотепер залишається актуальним твердження видатного американського мислителя минулого століття Д.Дьюї, що фундаментальна мета сучасної освіти полягає не в наданні учням інформації, а в тому, щоб розвивати їх критичний спосіб мислення, котрий дає змогу адекватно оцінювати нові обставини й формувати стратегію подолання проблем, які в них криються [9, с.84].

Отже, сучасна початкова школа має на меті виробити в учнів звичку вирішувати важливі питання, які виникають у житті, вчить формулювати, висловлювати і доводити свою думку та поважати думку інших. Модернізація системи освіти в Україні, зміна її орієнтирів на розвиток учнів як особистості, формування інтелектуального потенціалу та забезпечення постійного самовдосконалення, вимагає змін і в системі сучасної початкової освіти. Насамперед вона має бути зорієнтована на особистісний розвиток кожного учня відповідно до його здібностей. Саме в цих умовах особливого значення набуває проблема формування критичного мислення в учнів початкової школи [21, с.15].

Ідея розвитку критичного мислення виникла в США і є однією із загальновизнаних напрямів навчання та виховання у зарубіжній педагогіці та психології. Ця проблема стала об’єктом наукових пошуків як зарубіжних (Д.Брунер, М.Ліпман, Р.Пауль, Ч.Темпл, Д.Халперн, Дж.Гілфорд, К.Мередит, С.Заір-Бек, Дж.Чаффа, Д. Рассел, К.Уейд, К.Таврис та ін.), так і вітчизняних науковців (С.Терно, Б.Теплов, Н.Дайрі, О.Тягло, Т.Воропай, Д.Вількєєв, А.Федоров, А.Ліпкій, Л.Ямщикова, А.Авершин, Т.Яковенко, Б.Зейгарник, Т.Кудрявцев, І.Кожуховська, Н.Березанська та ін.).

Запорукою впровадження технології формування критичного мислення учнів у практику початкової школи є наукові доробки Л.О.Варзацької, М.С.Вашуленка, С.У.Гончаренка, О.Я.Савченко. У методичних працях педагоги висвітлювали питання розвитку в молодших школярів вміння самостійно опрацьовувати навчальний матеріал, виконувати проблемні завдання лінгвістичного спрямування, робити висновки, помічати та виправляти як власні помилки, так і помилки своїх однокласників.

На сьогодні визначено основні теоретичні засади й окреслено шляхи практичної реалізації розвитку критичного мислення учнів. Однак деякі аспекти цієї проблеми все ще залишаються недостатньо вивченими. Зокрема, проблема розвитку критичного мислення молодших школярів є актуальною та потребує більш глибокого дослідження.

Мета роботи - систематизувати та узагальнити педагогічні умови формування критичного мислення учнів початкових класів.

Об'єкт дослідження – розвиток критичного мислення учнів початкових класів.

Предмет дослідження – методика формування у дітей молодшого шкільного віку критичного мислення.

Завдання дослідження:

1. Вивчити наукові підходи до проблеми розвитку критичного мислення учнів.
2. Теоретично обґрунтувати методику формування критичного мислення учнів початкових класів.
3. Надати методичні рекомендації щодо формування критичного мислення учнів на уроках.

Для розв’язання поставлених завдань застосовувалися наступні методи дослідження, які взаємодоповнювалися та коригувалися: аналіз філософської, психолого-педагогічної, методичної літератури з проблеми дослідження для визначення ступеня дослідженості теми, мети, завдань дослідження, освітніх програм, підручників, нормативних документів; систематизація, узагальнення фактичного матеріалу з метою виділення й обґрунтування концептуальних положень за проблемою дослідження; синтез, порівняння, класифікація, абстрагування, конкретизація наукової інформації, які застосовувалися при визначенні понятійного апарату дослідження.

РОЗДІЛ 1. ТЕОРЕТИЧНІ ЗАСАДИ ФОРМУВАННЯ КРИТИЧНОГО МИСЛЕННЯ В УЧНІВ ПОЧАТКОВОЇ ШКОЛИ

1.1. Проблема формування критичного мислення в учнів у науковій літературі

Пріоритетним напрямом реформування системи початкової освіти, визначеним Л.Гриневич, є оновлення змісту освіти, зокрема в початковій школі. Школа має готувати учнів до життя, що можливо, на думку міністра освіти і науки України, через формування в школярів умінь критично мислити, працювати у команді, розв'язувати проблеми, самостійно шукати, аналізувати інформацію. Тому доцільно з’ясувати суть феномену «критичне мислення» і визначити шляхи його розвитку в учнів початкової школи [9, с.84].

Поняття критичного мислення досліджується у роботах Дж.Андерсон, К.Баханова, Дж.Браус, М.Векслер, Д.Вуда, Р.Джонсона, Р.Енніса, Д.Клустера, В.Мисан, О.Пометун, Н.Поспєлова, Р.Стернберга, Л.Терлецької, С.Терно, О.Тягло, Д.Халперн та ін.

Мислення - це нерозривно пов’язаний з мовою, соціально обумовлений, цілеспрямований психічний процес самостійного пошуку і відкриття істотно нового, тобто опосередкованого і узагальненого відображення дійсності в ході її аналізу і синтезу, що виникає на основі практичної дійсності із чуттєвого пізнання і далеко виходить за його межі [21, с.14]. Необхідність у мисленні виникає тоді, коли в процесі життя і практики у людини з’являється нова мета, нова проблема, нові обставини й умови діяльності.

Процес мислення - це активна цілеспрямована діяльність, в процесі якої здійснюється переробка наявної і нової інформації, відділення зовнішніх, випадкових, другорядних її елементів від основних, внутрішніх, що відображають суть досліджуваних ситуацій, розкривають закономірні зв’язки між ними [21, с.15].

Критичне мислення визначається Дж.Браусом і Д.Вудом як розумне рефлексивне мислення, яке сфокусоване на розв’язуванні питання щодо того що робити і що брати на віру. Люди, які здатні мислити критично в змозі визначати проблеми, які є явними або прихованими, визначати цілі, відшукувати інформацію, спостерігати, формулювати питання при пошуку нової інформації, зберігати у довготривалій пам’яті інформацію та її актуалізувати у потрібний момент, порівнювати, класифікувати та презентувати нову інформацію, аналізувати та встановлювати причинно-наслідкові зв’язки між поняттями та ідеями, ідентифікувати головні ідеї; ці люди здатні ідентифікувати помилки та виявити варіанти їх виправлення, вони володіють навичками переформулювання інформації, ідей; вміють висувати нові ідеї і бачити нові можливості, що дозволяє їм успішно розв’язувати проблеми. Не менш важливими є навички оцінювання, як-то формулювання критеріїв оцінювання інформації та ідей, перевірки тверджень [2, с.84].

На думку Д.Халперн критичне мислення вирізняється зваженістю, логічністю і цілеспрямованістю; людина, яка мислить критично використовує когнітивні навички та стратегії, які збільшують вірогідність одержання бажаного результату. Передумовами критичного мислення є готовність до планування, гнучкість, наполегливість, готовність виправляти свої помилки, усвідомленість, пошук компромісних розв’язань. Д.Халперн розкриває природу критичного мислення з точки зору його розвитку, в основі якого лежать навички критичного мислення - набір операцій, що дозволяють знайти шлях до мети, операцій, що лежать в основі уміння робити логічні висновки, аналізувати аргументи, перевіряти гіпотези, схвалювати рішення, оцінювати вірогідність подій [23, с.112].

Схожої думки дотримується Дж.Барелл. Характеризуючи людину, яка здатна мислити критично, наголошуючи на тому, що вона розв’язує проблеми, виявляючи наполегливість, контролюючи себе; відкрита для інших ідей, вирішує проблеми у співпраці з іншими людьми, прислуховуючись до співбесідника, позитивно відноситься до різних точок зору, навіть таких, що відрізняються від її власної, вона характеризуються терпимістю до невизначеності, емпатією; така людина розглядає проблеми з різних точок зору, встановлює множину зв’язків між явищами, розглядає кілька варіантів розв’язування проблеми, вміє будувати логічні умовиводи; розмірковує про власні думки, почуття, оцінюючи їх, прогнозує, визначає цілі, виявляє допитливість; така людина застосовує знання та навички в різноманітних ситуаціях, активно сприймає інформацію [9, с.85].

Дещо інакше визначає характеристики критичного мислення Л.Терлецька. Дослідниця наголошує на його глибині (проникливе мислення) - вміння проникати в суть, бачити неясне там, де іншим усе здається цілком ясним і зрозумілим; послідовності - уміння дотримуватися логічних правил, не суперечити самим собі, обґрунтовувати висновки; самостійності - уміння ставити питання, знаходити нові підходи до їх з'ясування; гнучкості - уміння змінювати спосіб розв'язання проблеми, знаходити нові шляхи, бути вільним від шаблону; швидкості - уміння швидко впоратися з пізнавальними завданнями; стратегічності - послідовне висування гіпотез, визначення ознак (сканування і фокусування) під час розв'язання завдань. Дещо інші ознаки критичного мислення виділяє Є.Полат, серед яких:

• аналітичність (відбір, порівняння, зіставлення фактів та явищ);
• асоціативність (установлення асоціацій з раніше вивченими фактами, явищами);
• самостійність;
• логічність (уміння будувати логіку доказовості розв'язання проблеми, послідовність дій);
• системність(уміння розглядати об'єкт, проблему в цілісності їх зв'язків і характеристик) [21, с.17].

Визначені українськими вченими ознаки критичного мислення, в цілому, корелюють з окремими характеристиками цього феномену, представленими у роботах американських та європейських науковців.

У контексті трактувань поняття критичного мислення закордонними вченими, дає визначення цього поняття С.Терно [21]. Автор характеризує критичне мислення як здатність використовувати певні прийоми обробки інформації, що дозволяють отримати бажаний результат; це вміння робити логічні умовиводи, приймати обґрунтовані рішення, оцінювати позитивні й негативні риси як отриманої інформації, так і самого розумового процесу. Нам більш імпонує визначення критичного мислення І.Бондарука як особливого типу мислення людини, спрямованого на самостійне розв’язання нею конкретної пізнавальної чи життєвої проблеми через її всебічний розгляд на основі різних джерел інформації, визначення шляхів розв’язання цієї проблеми, їх оцінювання й обґрунтованого вибору одного з них з постійною рефлексією та корекцією власної мисленнєвої діяльності визначає [21, с.56].

Здатність людини критично мислити ґрунтується на наявності в неї гарних дослідницьких навичок:

• спостереження (бачити і помічати властивості об'єкта);
• описування (зазначати, як об'єкт виглядає);
• порівняння (встановлювати подібності й розбіжності між об'єктами);
• оцінювання чого-небудь і порівняння з іншими речами;
• визначення (показувати чи доводити існування об'єкта);
• розпізнавання об'єкту як конкретну річ;
• асоціювання (розумово установлювати зв'язок між об'єктами);
• з'єднання об'єктів за принципом їхньої взаємодії;
• узагальнення (робити висновки на основі наявної інформації чи фактів);
• прогнозування (передбачати, що відбудеться в майбутньому);
• пророкування чого-небудь;
• застосовування (використовувати у відповідності);
• отримання практичної користі від чого-небудь [9, с.86].

1.2. Розвиток критичного мислення як засіб формування інтелектуальної культури учнів

Зазвичай, поняття "критичне мислення" пов'язують з пошуком недоліків, прорахунків. Коли ми говоримо: "Він мислить занадто критично", то маємо на увазі зайву недовірливість людини, її небажання приймати що-небудь на віру. Проте, в педагогічній науці та передовій педагогічній практиці цей термін найчастіше пов'язують із високим рівнем свідомості процесу навчання, причому не тільки з боку вчителя, але (що принципово важливо для освітньої технології розвитку критичного мислення) з боку учня. Педагоги-практики особливо виділяють цінність осмисленого навчання. Школяр, що вміє критично мислити, володіє різноманітними способами інтерпретації й оцінки навчальної інформації, здатний виділяти в тексті протиріччя й типи присутніх у ньому структур, аргументувати свій погляд, опираючись не тільки на логіку, але й на уяву співрозмовника. Такий учень почуває впевненість у роботі з різними типами інформації, може ефективно використовувати найрізноманітніші ресурси. На рівні цінностей, критично мислячий учень уміє ефективно взаємодіяти з інформаційним простором, принципово приймає можливість співіснування різноманітних поглядів в рамках загальнолюдських цінностей [9, с.88].

Відповідно пріоритетів діяльності МОН, метою середньої, зокрема, початкової освіти є формування в учнів критичного мислення. Критичне мислення починається з постановки запитань; воно спрямовано на визначення проблеми, на застосування знань й одержання результату; воно спирається на відоме знання, на пошук потрібної інформації, на досвід; воно прагне до оцінювання ситуації, до аналізу інформації, до переконливої аргументації. Критичне мислення характеризується усвідомленістю, логічністю, цілеспрямованістю і самостійністю [21, с.19].

Проблема розвитку критичного мислення учнів є актуальною у багатьох країнах світу. У США існує Інститут критичного мислення, фундатором якого є М.Ліпман, який підкреслює відповідність потреби розвитку критичного мислення завданню вдосконалення початкової, середньої та вищої освіти. Сучасний розвиток системи освіти в контексті проблеми критичного мислення, характеризується спрямуванням процесу навчання на осмислення навчального матеріалу; стимулюванням самостійного мислення учнів, а не репродуктивного вивчення наук, а також формуванням у них умінь складати і висловлювати власні судження. Розвиваючи критичне мислення учнів, у процесі навчання відбувається через залучення учнів до процесу активного навчання, коли вони не просто запам'ятовують навчальний матеріал, а й запитують, досліджують, творять, вирішують, інтерпретують та дебатують за його змістом (М.Ліпман) [21, с.24].

Технологія розвитку критичного мислення учнів упроваджується у багатьох країнах світу (М.Вайнстейн, А.Кроуфорд, М.Ліпман, С.Метьюз, Д.Макінстер, В.Саул, Ч.Темпл та інші), у тому числі й в Україні (К.Баханов, Т.Воропай, С.Мирошник, О.Пометун, Л.Терлецька, С.Терно, О.Тягло та інші). Оскільки критичне мислення розвивається шляхом розв'язування проблемних задач, робота над якими вимагає від учнів відповідального ставлення до ухвалення рішень (С.Терно), то технологія розвитку критичного мислення ґрунтується на теорії проблемного навчання, і, зокрема, на підходах до формування в учнів дослідницьких навичок [21, с.26].

Отже, технологія розвитку критичного мислення передбачає актуалізацію набутого досвіду, з’ясування неможливості застосування відомого знання і постановку проблеми, відшукання потрібної інформації або способу розв’язування проблемної ситуації, знайомство або відкриття нового знання або способу діяльності, зіставляючи з тим, що вже відомо, привласнення інформації, запам’ятовування її.

РОЗДІЛ 2. МЕТОДИКА ФОРМУВАННЯ У ДІТЕЙ МОЛОДШОГО ШКІЛЬНОГО ВІКУ КРИТИЧНОГО МИСЛЕННЯ

2.1. Система роботи з формування критичного мислення

в учнів початкових класів на уроках

Розглянемо можливості розвитку критичного мислення учнів початкової школи на уроках математики.

Чинний Державний стандарт початкової загальної освіти [6] та чинна програма з математики для 1-4 класів [11] передбачає формування в учнів початкової школи предметної математичної компетентності, яка виявляється як здатність учня (учениці) актуалізовувати і застосовувати досвід математичної діяльності у навчально-пізнавальних і практико-зорієнтованих ситуаціях. Для цього змістовою частиною програми для 1-4 класів визначено динаміку опанування молодшими школярами предметних-математичних компетенцій: обчислювальної, логічної, інформаційно-графічної, геометричної, алгебраїчної [15, с.68].

Відповідно до Державного стандарту початкової загальної освіти [6]  курс математики будується за такими змістовими лініями: числа, дії з числами; величини; математичні вирази, рівності, нерівності; сюжетні задачі; просторові відношення, геометричні фігури; робота з даними. Розглянемо можливості розвитку критичного мислення молодших школярів в процесі опанування цих змістових ліній.

Програма з математики побудована концентрично і передбачає поступове розширення множини чисел, в якій опановуються всі інші змістові лінії курсу. В межах змістової лінії «Числа і дії з числами» випадки обчислення поступово ускладнюються і передбачається ознайомлення учнів з різноманітними прийомами обчислення та формування в них гарної обчислювальної навички [9, с.90].

З метою розвитку критичного мислення учнів, вводячи наступні випадки обчислення, доцільно зіставляти їх з раніш вивченими, визначати відмінність, досліджувати вплив цієї відмінності на розв’язування, і у такий спосіб «відкриваючи» новий спосіб дії. Чинна програма з математики передбачає ознайомлення учнів з різними прийомами обчислення, що створює можливості для розвитку критичного мислення учнів через зіставлення різних прийомів обчислення, визначення спільного і відмінного в них, з’ясування доцільності застосування кожного прийому в окремих випадках обчислення [9, с.91].

Технологія розвитку критичного мислення учнів початкової школи при вивченні змістової лінії «Числа і дії з числами» може бути наступною:

• актуалізуємо відомий спосіб міркування при виконанні обчислень;
• змінюємо запис одного (обох) з компонентів арифметичної дії;
• з’ясовуємо як ця зміна вплине на розв’язування - чи можна міркувати у обчисленні так само, як і у першому випадку;
• намагаємось  застосувати відомий спосіб міркування; якщо стикаємось з неможливістю його використання в повному обсязі, вносимо корекцію в окремий крок міркування;
• рефлексуємо - аналізуємо як зміна запису числа (чисел) вплинула на розв’язування;
• рефлексуючи з приводу змісту власної діяльності, формулюємо орієнтувальну основу дії;
• застосовуємо новий спосіб дії [15, с.69].

На етапі застосування нового способу дії учням доцільно пропонувати неоднотипові завдання, щоб вони постійно вдавалися до розгорнутого орієнтування, критично оцінювали можливості застосування нового або раніш вивченого способу дії.

Корисними у чинній програмі з математики, з точки зору розвитку критичного мислення учнів, є наявність у змістовій лінії «Числа і дії з числами» (додаткові питання програми) можливості ознайомлення учнів з прийомами раціональних обчислень. Ці прийоми застосовуються лише для окремих випадків обчислення, тому учень має критично оцінити можливості використання у обчисленні певного прийому. Так, прийоми раціонального ділення на 5, 50, 500, 25, 250, 125 можливо застосувати лише у випадку, коли ділене закінчується певною кількістю нулів; а помножити на ці числа можна будь-яке число. Прийоми раціонального обчислення дозволяють учню досить швидко одержати результаті арифметичної дії, не вдаючись до письмових обчислень [9, с.92].

Також, для розвитку в учнів критичного мислення у систему завдань на повторення та закріплення знань та способів дії доцільно включати завдання з «пастками», завдання, які можна розв’язати без обчислень, способом логічних міркувань тощо [15, с.70].

Проаналізуємо відоме всім завдання "Продовж ряд чисел". (Ряд чисел — це послідовність чисел, запи­саних одне за одним за певним правилом).

Найяскравішим прикладом такої послідовності є натуральний ряд чисел. Вже першокласники зна­йомляться з відрізком цього ряду (від 1 до 100) та однією з його властивостей — кожне наступне чис­ло на 1 більше, ніж попереднє.

Запиши ще 5 чисел у цьому числовому ряді: 11, 12, 13, .... (34, 35, 36,...; 93, 94, 95,...).

Завданнями такого виду ми перевіряємо знання послідовності натуральних чисел на певному відріз­ку та вміння їх записувати, проте кожне з них має свою специфічну мету. Першим завданням переві­ряємо знання нумерації чисел певного десятка, у другому — вміння називати та записувати числа з переходом через десяток, у третьому — вміння запи­сувати числа на розряд більші від попереднього.

Які розумові дії виконує учень, щоб виконати це завдання? Він читає записані числа і спостерігає, як вони змінюються, тобто аналізує ряд чисел. З'ясовує, що кожне наступне число більше, ніж попереднє на 1, отже і для наступних чисел має зберегтися ця властивість.

Наступне завдання потребує такого самого алго­ритму розумових операцій, проте задіяні зовсім ін­ші математичні предметні вміння — вміння додава­ти/віднімати певне число.

Запиши ще 5 чисел у цьому числовому ряді: 2, 4, 6, ... (10, 20, 30, ...; 18, 16, 14, ...).

Такі завдання можна варіювати щодо різних чис­лових відрізків та різних правил укладання послі­довності. Проте обов'язково треба враховувати, якими математичними знаннями володіє учень.

У 2 класі коло математичних знань учня значно розширюється. Вивчення таблиць додавання з пе­реходом через десяток, ознайомлення з таблицями множення та ділення дає змогу ширше використо­вувати цей вид завдання.

Покажемо, як можна ускладнювати такий вид завдання за змістом і за формою.

Знайди зайве число і продовж ряд чисел: 2, 4, 6, 7, 8, 10, ....

Постав замість сніжинки цифру так, щоб це число не було зайвим у стовпчику:

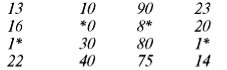
Продовж ряд чисел: 60, 59, 57, 54, 50, ...

Закресли одне число так, щоб ряд був складений за певним правилом. Запиши ще три числа за цим правилом.

84, 80, 76, 74, 72 _______________________

У 3/4 класі вивчаються числа у межах тисячі/ мільйона. Учні вже добре знають такий вид завдань і можуть працювати самостійно. Тут буде доречним ускладнити це завдання, а саме.

Продовж вліво і вправо числові послідовності:

..., 52, 65, 78, ...

., 24, 48, 96, ..

.., 100, 1000, 10000, ...

Перед учнем виникає проблема — треба визна­чити, скільки існує чисел у кожній послідовності, які можна записати зліва, і скільки справа. Для цього треба провести дослідження. Шляхом обчислень учні встановлюють, що кількість відомих чисел, які можна записати зліва, обмежена, а справа можна записати яку завгодно кількість чисел.

Вчитель може провести пропедевтичну бесіду про те, що і вліво можна продовжувати послідов­ності, бо існують числа, менші 0, і їх учні вивчати­муть у 6 класі.

Як бачимо, всі завдання однакового виду "про­довж ряд чисел" мають кожне свою специфіку, а це сприятиме розвитку вміння аналізувати математичні об'єкти: знаходити в них спільне та відмінне, встановлювати зв'язки між ними і в результаті вчитися знаходити шляхи розв'язування, навіть у ситуації, яка для них є невідомою.

Як же може виявитися вміння продовжувати ряд чисел у життєвій ситуації?

Андрійко живе в квартирі № 300. На поверсі зна­ходиться ще 5 квартир. Які можуть бути номери цих квартир?

Як дізнатися, на якому поверсі знаходиться квар­тира № 168, якщо на вхідних дверях у під'їзд висить табличка кв. №№ 141-176, а зайшовши в будинок ви дізналися, що на поверсі 4 квартири?

Відомо, що нумерація будинків ліворуч по вулиці є непарною. Яким буде по черзі будинок № 8, якщо руха­тися з початку вулиці?

Автобус із залізничного вокзалу в аеропорт від­правляється щогодини. Зараз закінчується посадка на рейс, що відбуде о 13 год. Назвіть час відправлення наступних трьох рейсів.

Завдання, які відображають реальні життєві ситуації або є гіпотетично наближеними до них, мають посісти чільне місце серед завдань, що вико­нуються на уроках математики.

Сприяють формуванню в учнів логічного склад­ника математичної компетентності і завдання з логіч­ним навантаженням, ребуси, головоломки тощо. Опишемо методику їх використання на уроках математики в початковій школі.

3 клас. Тема "Особливі випадки множення і ділення".

Після вивчення правил множення і ділення числа на 1 варто запропонувати учням завдання розшифруй ребуси. На дошці запис:

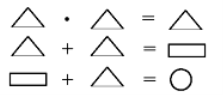
Завдання: розшифруй запис, якщо в рядках кожна фігура замінює число від 1 до 3.

Методичний коментар: варто спочатку запро­понувати учням самим розв'язати даний ребус. Можливо знайдуться такі, що зможуть відновити запис. Проте в обох випадках варто озвучити кожний крок міркування:

• Розглянемо перший рядок. Якими фігурами зашифровані числа? (Трикутниками).
• Скільки трикутників у цьому прикладі? (Три).
• Що це означає? (Що всі три числа однакові).
• Яким із запропонованих чисел можна заміни­ти трикутник? Діти з'ясовують, що це може бути тільки число 1.

На дошці поряд із ребусом з'являється запис: 1 · 1 = 1.

Другий приклад учням розв'язати дуже легко: замість трикутників записуються одиниці. Наголо­шуємо, що на етапі ознайомлення з таким видом завдань обов'язково проговорюється, чому саме ці числа — тому, що в попередньому прикладі ми з'ясу­вали,що трикутником позначається число 1. Поряд із ребусом з'являється запис: 1 + 1 = 2. Зрозуміло, що двійка позначена прямокутником. Аналогічні міркування проводяться і під час розшифрування третього рядка.

Наступні завдання цього виду ускладнюються: розшифруй запис, якщо в рядках кожна фігура замінює число від 1 до 5.

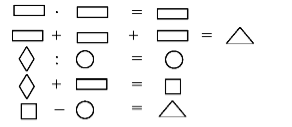
Методичний коментар: перші два рядки учні роз­шифрують з легкістю, аналогічно до попереднього завдання. Третій рядок викличе певну трудність. Щоб уникнути зайвих дій, запропонуйте учням записати на дошці, які фігури вже розшифровані. Така табличка має бути записана поряд із ребусом:

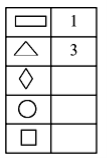
— Отже, залишилося дізнатися, якими фігурами позначені числа 2, 4 і 5. Які з них ми можемо запи­сати замість ромба та кола?

Учні відразу можуть здогадатися, що замість ромба треба записати четвірку, а замість кола — двійку. Проте, якщо ніхто не назве правильну відпо­відь, запропонуйте методом підстановки перевірити кожне число: два не поділиться ні на 4, ні на 5, отже замість ромба не можна записати двійку; 4 поді­литься на 2, але не поділиться на 5, отже замість ромба ми запишемо четвірку, а замість кола — двій­ку, бо 4 : 2 = 2 (на дошці відповідний запис і запис у таблиці). Залишається нерозшифрований квадрат і залишається число 5. Отже, квадрат — це 5. Під­ставляємо у приклад замість фігур числа і перевіря­ємо правильність записів.

1 · 1 = 1

1 + 1+ 1 = 3

4 : 2 = 2

4 + 1 = 5

5 - 2 = 3

Ці вправи є підготовчими до розшифрування ребусів, у яких не вказано, які числа зашифровано. Наприклад, такі. Розшифруй записи:

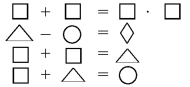
Методичний коментар: учитель має допомогти учням проаналізувати перший рядок.

• Скільки чисел записано в першому рядку? (Чотири).
• Які ці числа? (Однакові).
• Чому ви так думаєте? (Тому що однакові геометричні фігури позначають однакові числа).
• Назвіть окремо ліву і праву частини цієї рівності. (В лівій частині сума двох однакових чисел, а в правій — їх добуток).
• Як можна замінити суму однакових чисел? (Добутком).
• Давайте запишемо цей добуток. □ +□  = □  · 2.
• Хто здогадався, яке число позначає квадрат? (Число два).

Записуємо знайдене число у таблицю:

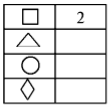
А навпроти першого рядка робимо запис: 2 + 2 = = 2 • 2.

Наступний крок у розв'язанні цієї задачі також потребує певних розумових зусиль. На відміну від попередніх завдань, треба розглядати не наступний — другий рядок ребусу, — а третій. Учитель дає змогу дітям самим знайти цей крок.

За розшифровкою третього рядка учні з'ясову­ють, що трикутник — це число 4, записують резуль­тат у таблицю, і відповідно третій рядок 2 + 2 = 4. За даними таблиці відновлюємо четвертий, а потім і другий рядки.

Як бачимо, розглянуті завдання містять відомі учням математичні знання, треба тільки встановити логічні зв'язки між даними і шуканими величина­ми. Це яскравий приклад того, що природніше за все логічну компетентність учнів формувати на уроках математики та інформатики, бо саме в цих навчальних предметах логічні форми і відношення виступають у найбільш чистому вигляді.

Ми вважаємо, що логічні завдання мають про­низувати весь зміст курсу математики та обов'язко­вого знаходити своє застосування на кожному уроці. Для цього необхідно вдосконалити чинну методику навчання математики.

На основі визначеного змісту логічної компе­тентності, вимог до рівня досягнень випускника початкової ланки освіти, дидактичних принципів навчання визначено методи формування логічної складової предметної математичної компетентності, а саме — евристичний, дослідницький та проблемно-пошуковий. За допомогою евристичного методу учні залучаються до процесу "відкриття" нових знань — понять, закономірностей, способів. Дослідницький метод забезпечує оволодіння способами наукового пізнання, формування у дітей здатності до творчої діяльності та потреби в ній.

Основним методом формування логічної компе­тентності має стати метод навчання в діяльності (проблемно-пошуковий метод), спрямований на розв'язування учнем навчальної проблеми (задачі), в якому засвоєння знань розглядають спільно з етапами засвоєння діяльності, тобто навчальна діяль­ність учнів поєднується з їхньою пізнавальною діяльністю.

Тільки під час знаходження виходу із проблем­ної ситуації відбувається встановлення міжпредметних зв'язків та інтегрування матеріалу із різних зміс­тових ліній, необхідних для розв'язання поставленої задачі; задіяне логічне мислення, яке передбачає вміння аналізувати, порівнювати, узагальнювати тощо; розвивається інтуїція, яка допомагає висува­ти найсміливіші гіпотези і при цьому формуються такі особистісно-цінні якості: розуміння того, що правильну відповідь можна знайти тільки аналізую­чи конкретну ситуацію; що кожний має право на помилку; толерантне ставлення до оточуючих.

Розглянемо методику використання іграшок для лічби, створен­ня ігрових ситуацій та проведення власне математичних ігор. У пер­шому класі іграшкові предмети використовуються в основному для лічби, у деяких випадках — і для формування математичних по­нять. Лічба предметів для дітей є цікавою, якщо вона потребує спо­стережливості, порівняння, виділення предметів з їх сукупності.

Ігри, не пов'язані з лічбою предметів, проводять під назвами: «Скіль­ки?»; «Жива нумерація»; «Зроби так»; «Продовж лічбу»; «Яке число пропущено?»: «Який по порядку?»; «Більше, менше, стільки ж» тощо. У вивченні першого десятка потрібно, щоб лічба і дії  над числами не тільки спиралися на дії з предметами. Не менш важливо, щоб дії з предметами збагачувалися у математичному відношенні. На пер­ших кроках навчання шестирічок перехід від оперування предмета­ми до роботи з числами, а потім до дій з числами є обов'язковим.

У процесі лічби такий перехід можна здійснювати на основі ви­моги: «Полічити трикутники і покласти стільки ж кружечків». Біля дошки можна застосувати ситуацію утруднення. Кружечків треба поставити стільки, скільки й паличок. Але кружечки такі великі, що їх не можна поставити в парі з паличками. Ряд кружечків виходить довгий.

Величина і колір іграшок не повинні затіняти математичну мету їх використання. Поступово у І класі треба перейти до використан­ня силуетних картинок тварин, овочів, фруктів, машин, інструмен­тів тощо. Частину таких силуетних картинок бажано мати і для індивідуальної роботи [16, с.118].

Застосовувати ігрові ситуації корисно під час розв'язування при­кладів і задач. З досвіду роботи відомо, що основним видом (будемо називати його першим видом) ігрової ситуації у першому класі є використання персонажів казок, мультфільмів, оповідань. Постанов­ка звичайних навчальних запитань і завдань з участю Незнайки, Бу­ратіно збуджує інтерес і підтримує активну діяльність кожної дити­ни протягом тривалого часу (5-7 хв.) [12, с.48].

Прийоми залучення знайомих дітям персонажів елементарно прості. Здебільшого використовується лялька для зображення дійо­вої особи. Її слова промовляє учитель. Суть ігрової ситуації з'ясовує­ться у вступній частині: «Незнайці треба знайти помилку»; «Бураті­но треба виручити з біди»; «Чебурашці треба допомогти розв'язати задачу». Далі йде формулювання завдання. Значна частина завдань використовується з підручника.

Варіаціями ігрової ситуації є читання листа від Буратіно, слу­хання прохання Незнайки, що звучить по телефону чи записане на магнітофонну плівку.

Другим видом ігрових ситуацій є використання у сюжеті задач дій тварин, наприклад: На галявині гралися троє зайченят. До них прибіли ще 2 зайчики. Скільки зайченят стало на галявині ?

Такі сюжети використовують не тільки для розв'язування задачі, а й для її складання.

До третього виду ігрових ситуацій відносять так звані лічилки або цікаві вправи. Це віршовані завдання. Зрозуміло, що заучувати їх напам'ять учням не слід.

До четвертого виду ігрових ситуацій належать ігри-змагання. Здебільшого це парні або групові змагання у розв'язуванні двох стовп­чиків прикладів та називанні таблиць арифметичних дій. Варіанти ігор бувають такі:

• хто більше і правильно розв'яже і запише відпо­відей прикладів за 1 хв.;
• хто швидше запише всі випадки складу чисел з двох доданків;
• хто більше назве прикладів із заданими результатами;
• хто безпомилково і чітко розкаже (запише) таблицю  додавання числа 3; 
• яка команда безпомилково назве таблицю віднімання числа 3.

В оцінюванні переможців треба знати міру. Не треба їх дуже хва­лити. Обов'язково слід знайти щось хороше і в "переможених" (усі вміють розв'язувати такі приклади) [16, с.119].

До п'ятого виду ігрових ситуацій відносять завдання ущільнено­го характеру. Цей вид добре ілюструють такі ігри: "Доповнити до числа 5", «Магазин», “Риболов» тощо.

До шостого виду ігрових ситуацій належать власне математичні ігри. У першому класі це "Кругові приклади”, “Лото", "Доміно". Усі вони на додавання і віднімання чисел в межах 10. "Кругові приклади" розв'язують одночасно всі учні, причому самостійно. Гра в  лото проводиться на основі індивідуальних карток або на основі   натурального ряду чисел від 1 до 10. В останньому випадку вчитель диктує приклад, а учень в натуральному ряді закриває фішкою (кружечком) те число, яке є відповіддю цього прикладу. Якщо відповідь   повторюється, то учень кладе на число дві фішки. «Доміно» у 1 -му   класі використовується як парна гра, тому для її проведення потріб­но мати відповідну кількість наборів такої гри[12, с.49].

У практичній роботі використовуються казки, проводяться ігри на відгадування, на розпізнавання фігур чи їх зміну, на кмітли­вість (яка спирається на кількісну характеристику) тощо. Ігрових ситуацій можна створити багато,  але всі вони мають підпорядкува­тись головній меті — учень має працювати над математичними за­вданнями.

Також основу курсу математики становить вивчення арифметики цілих невід’ємних чисел й основних величин, навколо чого здійснюється формування вміння розв’язувати сюжетні математичні задачі та алгебраїчна і геометрична пропедевтика.

Послідовність вивчення нумерації чисел і арифметичних дій над числами та величинами передбачає наступний порядок по роках навчан­ня: 1 клас - числа та арифметичні дії додавання і віднімання без пере­ходу через розряд у концентрах «Десяток», «Сотня»; 2 клас - вивчен­ня арифметичних дій додавання і віднімання з переходом через розряд відповідно до двох етапів: додавання й віднімання з переходом через десяток в межах 20 (табличне) і додавання й віднімання з переходом через десяток в межах 100; вводиться конкретний зміст арифметичних дій множення та ділення, вивчаються закони множення; наступним кро­ком є опанування учнями табличного множення і ділення, причому всі таблиці пропонуються у 2-му класі; зміст навчального матеріалу 3-го класу будується у концентрі «Тисяча»: крім усних прийомів додавання і віднімання, вводиться письмовий прийом, тоді як у попередній про­грамі письмовий прийом пропонувався в концентрі «Сотня». В учнів формують навички поза табличного множення і ділення, причому про­тягом навчального року, а не наприкінці його, як це було раніше. В учнів формуються навички позатабличного множення та ділення, причому протягом навчального року, а не наприкінці його, як це було раніше. Ви­падки множення або ділення круглого числа на одноцифрове, ділення круглого на кругле число вводяться ще в межах вивчення нумерації три- цифрових чисел; 4-й клас - концентр «Мільйон»: нумерація багато-цифрових чисел розглядається як побудова десяткової системи числення, а не через нарощування розрядів, що дозволяє заощадити час на вивчення інших питань програми. Також у 4-му класі розглядаються арифметичні дії додавання й віднімання, множення та ділення над багатоцифровими числами.

У першому класі учні опановують нумерацію чисел першого десят­ка; у дітей формується поняття про число як кількісну характеристику класу скінчених еквівалентних множин, діти навчаються їх порівнювати та вчать склад чисел [3].

На відміну від попередньої програми, додавання розглядається як знаходження кількості елементів об’єднання множин, що не перетина­ються; віднімання як знаходження кількості елементів множини, які за­лишилися після вилучення її частини. Пропонується також для вивчен­ня додавання й віднімання за числовим променем.

Перед складанням таблиць додавання і віднімання в межах 10 передбачається формування відповідних обчислювальних прийомів: додавання і віднімання чисел 2-5 виконується частинами; додавання чисел другого п’ятка - на основі переставного закону додавання; від­німання чисел другого п’ятка - на основі взаємозв’язку між діями до­давання і віднімання. Таким чином, наголошується на тому, що учні повинні володіти обчислювальними навичками, а не лише знати та­бличні результати.

Відмінною особливістю нової програми є те, що при вивченні та­блиць додавання і віднімання в межах 10 звертається увага на характер зміни суми в залежності від зміни одного з доданків та на характер зміни різниці в залежності від зміни зменшуваного, чого не було в попередній програмі.

Таблиці додавання і віднімання є гарним матеріалом для висновків про залежність результату від зміни одного з компонентів при сталому іншому. Ці знання є важливими з огляду на пропедевтику функціональ­ної залежності, розвитку функціонального мислення дитини.

Вивчення нумерації в концентрі «Сотня» відбувається за трьома етапами: числа, подані у круглих десятках; числа 11 - 20, числа 21 - 100. Причому, вивчення нумерації в межах 100 в 1-му класі не розривається на два етапи - 11 - 20 та 21 - 100, що дозволяє заощадити час на вивчен­ня аналогічних питань теми [4].

Діти приходять до школи, знаючи назви чисел не лише в межах 20, а й до 100. Тому недоцільним є обмеження лише вивченням нумерації чисел від 11 до 20, як було у попередній програмі. Хоча числа від 11 до 20 відрізняються від решти двоцифрових чисел тим, що в них порядок читання та запису не збігається, але їх нумерація, так само, як і нумера­ція чисел 21 -100, заснована на десятковому складі числа і на позицій­ному принципі запису. Отже, немає сенсу вивчати двічі майже один й той самий матеріал.

Відмінною особливістю нової програми є вивчення додавання й віднімання двоцифрових чисел без переходу через розряд у 1-му класі за­мість табличного додавання й віднімання в межах 20, як було у попере­дній програмі.

Такий підхід вважаємо доцільним, оскільки на цьому матеріалі від­бувається закріплення знання таблиць у межах 10 (десятки додають до десятків, одиниці до одиниць). Впевнені, що це заощадить час і надасть можливість у 2-му класі більше уваги приділити формуванню в дітей об­числювальних навичок додавання і віднімання з переходом через десяток.

Кожна змістовна лінія програми для певного року навчання почи­нається з узагальнення й систематизації знань учнів. Якщо порівняти результати навчальних досягнень учнів з цих питань на попередньому етапі навчання, то можна помітити, що йде ще й розвиток, приріст компетентності дітей. Проілюструємо це на прикладі арифметичних дій додавання і віднімання двоцифрових чисел без переходу через розряд (у 1-му та 2-му класах). Щодо додавання й віднімання в 1-му класі ви­значено, що учень має уявлення про сутність порозрядного додавання і віднімання двоцифрових чисел без переходу через десяток; застосовує прийоми обчислення у межах 100 без переходу через розряд. А в 2-му класі визначено вимогу володіння обчислювальними навичками дода­вання і віднімання без переходу через десяток у межах 100.

При вивченні додавання і віднімання з переходом через десяток у межах 20 передбачається формування обчислювальних прийомів дода­вання і віднімання. Вважаємо недоцільним лише запам’ятовування та­бличних результатів, як це було передбачено попередньою програмою.

При складанні таблиць додавання і віднімання з переходом через десяток продовжується формування в учнів уявлення про залежність суми від зміни одного доданка при сталому другому, про залежність різниці від зміни зменшуваного при сталому від’ємнику.

Новою програмою передбачене формування обчислювальних при­йомів додавання і віднімання двоцифрових чисел з переходом через роз­ряд. Вивчення теоретичних основ обчислювальних прийомів здійсню­ється на рівні ознайомлення. Це важливо, зважаючи на наукові засади формування обчислювальних навичок - досконалого володіння обчис­лювальним прийомом. Тому у результативній частині як кінцеву мету визначено вимогу-володіння обчислювальними навичками.

Перед вивченням таблиць множення і ділення відбувається ознайом­лення учнів з такими питаннями: множення і ділення на 10, множення і ділення чисел 0 та 1, неможливість ділення на нуль. Знання учнями пра­вила множення числа на 10 дозволить відтворювати результат множен­ня будь-якого числа на 9 на основі знання наступного результату (саме «нижню» частину таблиці множення діти запам’ятовують найгірше).

Відповідно з новою програмою усі таблиці множення і ділення вивчаються в 2-му класі, тоді як у попередній програмі вони були «роз­биті» на два роки навчання. За підходом, що передбачався попередньою програмою, вчителі задавали на літні канікули учням вивчити решту таблиць, що призводило до механічного їх заучування, тоді як таблиці множення і ділення - це гарний матеріал для спостереження дітьми ха­рактеру зміни добутку залежно від зміни одного з множників та харак­теру зміни частки в залежності від зміни діленого при сталому дільнику. Крім того, учні повинні мати уявлення про способи складання таблиць множення і ділення, визначити певні закономірності у їх побудові.

Нумерація чисел у концентрах «сотня», «тисяча», «мільйон» розглядається через введення нової лічильної одиниці, лічбу новою лічильною одиницею, порівняння, додавання й віднімання (множення та ділення) чисел, поданих у новій лічильній одиниці.

Серед арифметичних дій на основі нумерації розглядається не лише додавання й віднімання на засадах порядку слідування чисел при лічбі або десяткового складу чисел, а множення та ділення. Наприклад, при вивченні арифметичних дій на основі нумерації трицифрових чисел формується уміння виконувати множення й ділення шляхом укрупнен­ня розрядних одиниць, множення та ділення із застосуванням правил множення числа на добуток і ділення числа на добуток. Це є доцільним і виправданим з точки зору загального уявлення про десяткову систему числення.

Окремо виділено прийоми усного додавання й віднімання на ма­теріалі круглих чисел та письмові прийоми. Водночас слід зазначити, що письмові прийоми додавання й віднімання вперше вводяться лише у концентрі «тисяча», тоді як у попередній програмі вони вводилися в концентрі «сотня». Ми виходили з того, якщо діти добре засвоїли усні прийоми додавання і віднімання в межах 100, то вони не лічать у стовп­чик, а відразу пишуть відповідь - таким чином, змінюється не спосіб міркування, а форма запису; якщо діти не оволоділи обчислювальними навичками усного додавання і віднімання, то, познайомившись з пись­мовими прийомами, вони вже й не намагаються лічити усно.

Вивчення випадків позатабличного множення і ділення «розтягну­то» у часі. Ще у межах арифметичних дій на підставі нумерації три- цифрових чисел діти ознайомилися із випадками множення та ділення круглого числа на одноцифрове, діленням круглого числа на кругле.

Вивчення теми «Усні прийоми множення і ділення (позатабличні)» розпочинається із ознайомлення молодших школярів із діленням з остачею, тоді як це питання було останнім у темі в попередній про­грамі. Це є корисним, по-перше, з огляду на те, що ділення з остачею виконується на основі змісту дії ділення на вміщення, і, таким чином, ми ще раз маємо нагоду звернутися до конкретного змісту дії ділення; по-друге, ділення з остачею є основою письмового ділення, яке являє собою ланцюжок ділень з остачею, і для його повноцінного засвоєння потрібний час.

На відміну від попередньої програми введено питання про раціо­нальні обчислення. Правила множення та ділення на 5, 50, 25; множення на 11, 9, 99, що значно полегшує дітям окремі випадки обчислення.

У новій програмі письмові прийоми множення і ділення вводяться на матеріалі трицифрових чисел, а потім переносяться на багатоцифрові. Це дозволяє «розтягнути» вивчення досить складних для дітей дій на тривалий час.

Ознайомлення з математичними виразами «сума» і «різниця»; читан­ня і запис математичних виразів відбувається в 1-му класі. Формується поняття про істинні та хибні рівності й нерівності, вводяться способи порівняння числа і математичного виразу та двох математичних виразів.

У 2-му класі передбачено формування поняття про математичні ви­рази «добуток» і «частка», їх читання і запис; порівняння математичних виразів за допомогою обчислення їх значень або на основі знань про залежність результату від зміни одного з компонентів. Таким чином, забезпечується формування в учнів знання математичної термінології, розвиток математичного мовлення, логічного мислення.

Відповідно до нової програми в 3-му класі передбачено ознайомлен­ня з поняттям «рівняння», «розв’язок (корінь) рівняння», що дозволяє прослідкувати наступність із курсом математики 5-го класу, де учні бу­дуть оперувати цими термінами.

Крім того, відразу після ознайомлення з простими рівняннями вво­дяться складніші рівняння (права частина яких подана числовим вира­зом, один із компонентів - числовий вираз). Оскільки попередня про­грама передбачала складніші рівняння розглядати наприкінці 4-го класу, й в учнів формувалося уявлення про те, що рівняння має лише простий вигляд. За такого підходу вчителю було дуже складно донести до учнів думку про існування рівнянь ускладненої структури, а дітям зрозуміти, як складніше рівняння звести до простого. За таких умов не відбувалося повноцінного формування вмінь розв’язування складніших рівнянь.

У 4-му класі діти мають розв’язувати й ті рівняння, в яких один з компонентів - вираз зі змінною, що не було передбачено попередньою програмою. Треба зазначити, що в 5-му класі пропонуються здебільшо­го рівняння такої структури.

Щодо нерівностей із змінною, тут формується в школярів уявлення про множинність її розв’язків, про розв’язування нерівностей способом добору. Позитивним є те, що в додаткових питаннях програми перед­бачено вивчення ще й інших способів розв’язування нерівностей: зве­денням до рівняння та логічним способом, що виправдано з огляду на реалізацію наступності між початковою та основною школою.

Змістова лінія «Сюжетні задачі» також містить можливості для розвитку критичного мислення молодших школярів. Так, програмою для 1-го класу передбачено формування в учнів поняття задачі, а це означає потребу вміщення у підручниках завдань на підведення під поняття «задача», за допомогою яких учні мають критично оцінювати чи є даний текст задачею. Відповідно до чинної програми, в роботі над простими задачами, учні обов’язково мають аналізувати текст задачі, оцінюючи більше чи менше число одержать у відповіді на її запитання (прикидка очікуваної відповіді), обґрунтовувати вибір арифметичної дії, і лише потім записувати розв’язання задачі. Далі в 2-му класі, після ознайомлення зі складеною задачею, учні критично оцінюють можливість розв’язати задачу однією дією, і в залежності від відповіді на це запитання визначають вид задачі: проста чи складена [15, с.71]. Різноманіття математичних структур складених задач дозволяє авторам підручників реалізувати таку методику розгляду складених задач, коли наступна (ускладнена) задача подається у співставленні з такою, яку діти вже добре вміють розв’язувати; коли нові види задач вводяться шляхом зміни запитання відомої задачі, або зміни її умови. Технологія розвитку критичного мислення учнів при формуванні в них вміння розв'язувати складені задачі може бути такою:

• розв’язування задачі відомої математичної структури;
• зміна її запитання або умови;
• зіставлення одержаної задачі з попередньою і визначення відмінності;
• дослідження впливу відмінності на розв’язання одержаної задачі;
• розв’язування одержаної задачі [15, с.72].

Починаючи з 3-го класу учні знайомляться з типовими задачами: задачами, що містять однакову величину (задачі на знаходження четвертого пропорційного, на пропорційне ділення, на знаходження невідомих за двома різницями, на подвійне зведення до одиниці) та задачами на процеси ( задачі на спільну роботу, задачі на рух). Формування в учнів вміння розв’язувати типові задачі можливе шляхом дослідження їх математичних структур та способу розв’язування [9, с.93].

Технологія розвитку критичного мислення учнів під час навчання розв'язування задач, що містять однакову величину може бути наступною:

• розв’язування задачі (задач) відомої математичної структури;
• зміна умови і запитання розв’язаних задач, одержання задач нової математичної структури;
• зіставлення задач та визначення спільного та відмінного в них;
• дослідження впливу відмінності, між одержаною задачею та раніш вивченою, на розв’язання задачі, розв’язання задачі;
• зміна ситуації задачі і дослідження її впливу на розв’язання задачі;
• зміна числових даних задачі і дослідження її впливу на розв’язання задачі;
• зміна шуканих задачі і дослідження її впливу на розв’язання задачі;
• зміна однакової величини і дослідження її впливу на розв’язання задачі [21, с.31].

Слід зазначити, що поступово узагальнюючи математичні структури задачі та плани їх розв'язування (на певних етапах дослідження), учні, нарешті, узагальнюють математичну структуру задач певного типу та план їх розв’язування.

У процесі роботи над окремою задачею, що містить однакову величину, для розвитку критичного мислення молодших школярів, треба стимулювати учнів робити прикидку очікуваного результату, ще до розв'язування задачі. Це можливо завдяки тому, що програмою у змістовій лінії «Величини» передбачено ознайомлення учнів з групами взаємопов’язаних величин та залежностями між ними [9, с.94].

Аналогічною є технологія розвитку критичного мислення учнів під час навчання розв'язування задач на процеси. Так, формуючи уміння розв’язувати задачі на спільну роботу, з метою розвитку критичного мислення,доцільно:

• розв’язати просту задачу, я якій шуканою є продуктивність спільної праці двох виконавців;
• продовжити її, змінивши запитання;
• дослідити як ця зміна вплине на розв’язування і розв’язати одержану задачу;
• змінити ситуацію задачі та дослідити вплив цієї зміни на розв’язання задачі;
• змінити числові дані задачі і дослідити вплив цієї зміни на план розв’язування задачі;
• змінити шукане і дослідити...;
• рефрексуючи, узагальнити математичну структуру та план розв’язуван-ня задач даної математичної структури;
• змінити умову задачі, ускладнивши її, і дослідити вплив зміни умови на розв’язання задачі;
• змінити характер дій виконавців та дослідити вплив цієї зміни на спосіб знаходження продуктивності спільної праці [15, с.73].

В результаті такого дослідження задач відбувається узагальнення математичної структури та плану розв’язування задач на спільну роботу.

Дослідження задач на рух відбувається за наступними змінами: за зміною напрямку руху тіл, за зміною числових даних, за зміною шуканих.

Корисним з точки зору розвитку критичного мислення учнів є зіставлення задач споріднених типів ( в межах однієї групи) й дослідження спільного та відмінного в їх математичних структурах та з’ясування впливу відмінності на розв’язування задач, що в решті призводить до узагальнення способу розв’язування задач певної групи [9, с.95].

Можливість деякі задачі розв’язати кількома способами, так само, треба обов’язково реалізовувати з метою розвитку критичного мислення учнів. Так, задачі на знаходження четвертого пропорційного можна розв’язати способом знаходження однакової величини та/або способом відношень. Так, розв’язавши задачу двома способами, можна змінити одне з числових даних, що унеможливлює застосування одного з них, рефлексуючи, учні відкривають можливості застосування певних способів при розв’язуванні: способу знаходження однакової величини та способу відношень [15, с.74].

Подані вище технології реалізовані у лінійці підручників і навчальних зошитів з математики для 1-4-го класів С.Скворцової та О.Онопрієнко [15]. Вже сьогодні, у цих доробках реалізовано мету розвитку критичного мислення учнів, шляхом подання системи навчальних задач, в якій учні занурюються у дослідження і «відкривають» нові знання та способи дії, рефлексуюючи формулюють орієнтувальну основу нової дії; коли задачі пропонуються не поодиноко, а у передбачають зіставлення пари-трійки схожих за сюжетом, але різних за математичною структурою задач тощо. Все це сприяє розвитку критичного мислення учнів.

Отже, реалізація мети формування в учнів початкової школи критичного мислення, здебільше, лежить у площині методики навчання та технологій проведення уроків, оскільки програмою з математики визначено зміст, який є доцільним для розвитку критичного мислення молодших школярів.

Загальна технологія розвитку критичного мислення учнів початкової школи має реалізовуватись в усіх змістових лініях початкового курсу математики і передбачати:

• розв’язування завдання на актуалізацію відомого знання або способу дії;
• внесення змін у зміст завдання; зіставлення одержаного завдання з раніш розв’язаним, визначення спільного і відмінного;
• з’ясування можливостей застосування відомого способу дії до одержаного завдання, за потреби його корегування;
• дослідження математичного об'єкта шляхом зміни неістотних ознак, визначення впливу певної зміни на розв'язання;
• рефлексія власної діяльності і відкриття нового знання або способу дії, формулювання орієнтувальної основи дії;
• привласнення нового знання або способу дії шляхом виконання діяльності з новим змістом. Можливе циклічне повторення з п. 2) [9, с.96].

Між тим, подана загальна технологія стосується лише етапу ознайомлення учнів з новим знанням або способом дії, але робота над розвитком критичного мислення учнів не має обмежуватися лише даним етапом. На етапі формування вмінь та навичок учитель має пропонувати учням спеціальні завдання, які передбачають дослідження, завдання з пастками тощо.

Наведемо кілька прикладів розвитку критичного мислення учнів початкової школи на уроках української (рідної) мови та читання.

Так, актуалізацію опорних знань молодших школярів із теми “Повторення  вивченого про іменник” (блок уроку - евокація) доцільно організувати за допомогою методичних стратегій “Асоціативний кущ” або “Кубування”. Наприклад, на підсумковому уроці з української мови в четвертому класі з названої вище теми вчитель може запропонувати учням текст із виділеними словами - іменниками. Не даючи запитань школярам, а лише демонструючи грані куба, педагог ставить завдання: усно схарактеризувати виділені слова, що і буде підсумком за темою “Іменник”. Вважаємо, що на гранях куба варто зробити такі записи:

• частина мови,
• запитання,
• рід,
• число,
• відмінок,
• член речення [1, с.103].

На етапі осмислення (вивчення нового матеріалу) доцільно використати ряд методів, а саме: читання тексту із системою позначок “Допомога”, “Мозаїка “Джигсоу”, “Запитання - відповідь”, “Знаємо - хочемо дізнатись - дізналися”, взаємонавчання, метод “Прес” тощо. Схарактеризуємо деякі з них [4, с.11].

Наприклад, “Мозаїка ”Джигсоу” - методична стратегія, спрямована на взаємонавчання, згідно з якою учні працюють у групах. Ця стратегія передбачає вивчення нового матеріалу за допомогою шести так званих кроків. Зокрема, під час вивчення казки “Лисичка-кума” у 4 класі організація роботи учнів відбувається так:

• клас поділяється на групи чисельністю 3-5 осіб (так звані “домашні групи”); кожен учасник одержує номер від 1 до 5;
• учням пропонується, наприклад, текст казки й учитель пояснює, що вся група має усвідомити зміст тексту, який вивчатиметься частинами;
• текст казки поділяється на логічно завершені частини; учні з однаковими номерами збираються в експертні групи;
• кожна група досконало вивчає свою текстову частину казки;
• учні повертаються до своїх домашніх груп;
• на цьому етапі відбувається повне вивчення тексту казки; кожен учень має розповісти зміст своєї частини, для того, щоб всі члени групи мали змогу дати відповіді на запитання до тексту; потім учитель перевіряє, наскільки діти усвідомили зміст казки - на питання дають відповіді всі члени групи, окрім учня, який був відповідальним за вивчення певної частини тексту [6, с.71].

На нашу думку, усвідомленню третьокласниками головної думки оповідання Є.Гуцала “Перебите крило” і розвитку в них критичного мислення сприятиме метод “Прес”. Загальновідомо, що ця стратегія покликана навчити дітей знаходити вагомі аргументи і формулювати власну думку щодо конкретного питання, а також чітко та логічно структурувати ідеї, що виникають.

Застосування пропонованого методу відбувається за чотирма етапами, а саме:

• учень висловлює свою думку “Я вважаю...”;
• молодший школяр пояснює причину такої точки зору: “Тому що….”;
• дитина наводить приклад додаткових аргументів на підтримку своєї позиції: “Наприклад….”;
• учень початкової школи узагальнює, формулює висновки: “Отже…”.

Так, виконуючи пропоноване вище завдання діти мають побудувати свою аргументовану відповідь такі:

1. Я вважаю, що Олег зрозумів свою провину.
2. Тому що він переживав, що заподіяв лихо лелекам.
3. Наприклад, про це свідчать його вчинки, описані в оповіданні: “Надто вже часто той прибігав і допитувався за лелек: а як там крило, а може, їсти щось принести, то він миттю”.
4. Отже, треба берегти природу, тварин, птахів і допомагати їм у скрутну хвилину.

Цей метод може бути використаний педагогом і на інших етапах уроку.

Стратегії “Ромашка запитань Блума”, “Кола Вена”, “Сенкан”, асоціатив-ний кущ тощо дозволяють належним чином організувати такий блок уроку, як рефлексія (розмірковування). Наприклад, на останньому етапі уроку літературного читання в 2 класі, присвяченому вивченню літературних казок, за допомогою діаграми Вена (“Кола Вена”) можна з’ясувати, чи усвідомлюють молодші школярі, у чому полягає відмінність між літературною та народною казкою, оскільки ця стратегія допомагає навчити дітей зіставляти, порівнювати, знаходити спільні риси й ознаки між явищами та поняттями. Організувати діяльність на уроці доцільно так:

• учитель об’єднує учнів у пари й дає завдання;
• учні заповнюють діаграму Вена. Для цього будують два (чи більше) великі кола, які частково накладаються одне на одне так, що посередині утворюється спільний простір, у якому міститиметься інформація, властива обом групам предметів, які порівнюються [3, с.69].

Перевірити рівень сформованості вмінь і навичок учнів допоможуть технології “Ромашка запитань Блума”, “Хрестики-нулики” тощо.

Так, однією з популярних у світі методик є стратегія “Ромашка запитань Блума”, створена відомим американським психологом і педагогом Бенджамі-номБлумом з метою формування в дітей рівнів пізнавальної самостійності (знання, розуміння, застосування, аналіз, синтез і оцінка). Суть цієї методики полягає в тому, що перед молодшими школярами ставиться завдання чи пропонується тема, яку необхідно вивчити. Для глибшого розуміння матеріалу вчитель пропонує дітям серію із шести типів запитань (прості, уточнювальні, інтерпретаційні (пояснювальні), творчі, оцінювальні, практичні). З метою унаочнення і кращого сприйняття ними завдання варто намалювати ромашку і записати запитання на її пелюстках (кожному типу запитання має відповідати одна пелюстка) [1, с.104].

Так, з’ясувати, чи сформовані в третьокласників уміння й навички розрізняти форми слова і спільнокореневі слова (тема “Спільнокореневі слова. Корінь слова”) можна за допомогою поданих нижче запитань, написаних на пелюстках “Ромашки запитань Блума”:

• Що називається коренем слова?
• Тобто ти вважаєш, що слова школяр, шкільний, школа, (у) школі є спорідненими?
• Чому подані слова не можна вважати спільнокореневими?
• Чи змінилося б значення слова ліс, якби ми додали до нього суфікс - ок?
• Чим відрізняються форми слова від спільнокореневих слів?
• Як можна запобігти такої помилки як близьке вживання спільно-кореневих слів-іменників і форм одного і того ж слова?

Не менш цікавою, на нашу думку, є стратегія “Хрестики-нулики”, яка може бути використана в кінці уроку і являє собою своєрідний диктант. У цьому випадку рефлексію організовують так: учитель повільно читає завдання, при цьому одразу пропонує відповідь; після паузи учні записують відповідь у поданій формі, що зовні нагадує таблицю, певним чином (якщо вони згодні з твердженням учителя, - ставлять хрестик, якщо ні - нуль); діти заздалегідь поінформовані, що починати записувати відповіді потрібно з верхньої лівої клітинки, поступово рухаючись праворуч [1, с.105].

На етапі вивчення нового матеріалу важливою для розвитку критичного мислення є технологія «Дошка запитань». Суть її в тому, що на стіні класу вивішується великий аркуш паперу, на якому вчитель просить учнів записувати будь-які запитання, що виникають у них під час сприймання й усвідомлення та осмислення нових знань. Ця технологія стимулює природну допитливість школярів, розвиває вміння ставити запитання, привчає не відволікатися від теми уроку, а вчитель має можливість побачити, що з вивченого залишилося незрозумілим.

На підсумковому етапі уроку рідної мови доцільною буде діаграма Ейлера-Вена. Ця технологія передбачає створення графічної схеми з двох чи трьох кіл, які частково накладаються одне на одне.

На прикладі теми «Відмінювання прикметників чоловічого і середнього роду» розглянемо побудову діаграми. Малюємо два кола, які накладаються одне на одного. У перетині  кіл записуємо спільне у відмінюванні прикметників в обох родів; у лівій — закінчення, характерні лише для прикметників чоловічого роду; у частині, обмеженій правим колом, записуємо закінчення, характерні лише для прикметників середнього роду.

Важливим є підсумковий етап уроку, на якому вчителю необхідно організувати зворотній зв’язок зі школярами для того, щоб дізнатися, як кожен учень засвоїв матеріал. Це можна зробити за допомогою твору-п’ятихвилинки (есе) — вільного, особистого трактування певної теми [4, с.5].

Якщо є час, варто переглянути твори, вибрати з них цікаві запитання, відповіді. Можна почати наступний урок посиланням на ці есе , сказавши: «На попередньому уроці залишилося незрозумілим...». Таким чином педагог демонструє повагу до думок учнів, а школярі не будуть боятися чогось не зрозуміти.

Вважаємо, що використання на підсумковому етапі твору-п’яти-хвилинки більш доцільне, ніж усне опитування, оскільки дає змогу визначити рівень засвоєння теми кожним учнем [3, с.69].

Значні можливості для розвитку критичного мислення мають уроки читання. У працях педагогів щодо розвитку критичного мислення учнів часто вживається термін «критичне читання», який трактують як спосіб опрацювання текстів, коли учні не читають твір механічно, а застосовують під час читання розумові операції високого рівня, що дозволяє сформулювати власну думку щодо інформації. Фахівці вважають, що навчити школяра критичного читання — одна зі складових формування компетентного учня.

Підручники з читання, зокрема навчальні тексти як важливі структурні компоненти цих навчальних книг, є для учнів основним джерелом знань. Тому так важливо навчити школярів працювати з текстами підручників. Розглянемо технології, за допомогою яких молодші школярі оволодівають зазначеним умінням, що сприятиме їх подальшому навчанню.

У читанках для початкової школи є достатня кількість науково-пізнавальних статей, для роботи з якими можна використати зазначену вище технологію «Знаємо — Хочемо дізнатися — Дізналися». Крім цього, можна застосовувати описану технологію і при читанні інших друкованих матеріалів — навчальних посібників, енциклопедій, газетних і журнальних статей.

При опрацюванні науково-пізнавальних статей доречною є технологія «Читання тексту з позначками», в основу якої покладено читання матеріалу з одночасним маркуванням окремих його частин спеціальними позначками на полях і заповненням таблиці [6, с.71].

Ця стратегія потребує певного часу, однак учні більш глибоко вивчають текст підручника, навчаються класифікувати інформацію. Критеріями диференціації навчальної інформації є самі позначки. Під час обговорення школярі формулюють висновки щодо прочитаного. Стратегію «Читання тексту з позначками» на перших порах слід використовувати у процесі колективної діяльності, але з часом її можна давати як домашнє читання. У початкових класах за такою технологією доцільно опрацьовувати навчально- пізнавальні тексти, нариси, статті тощо [4, с.5].

Технологія «Читання в парі — узагальнення в парі» розрахована на читання тексту в парах і є ефективною, коли твір складний для розуміння або перевантажений фактичним матеріалом [2]. Щоб організувати діяльність, варто обрати текст, розбити його на логічні частини; об’єднати учнів у пари, дати чіткі пояснення, що вони мають робити. Наприклад, перед читанням оповідання Тамари Коломієць «Хліб» (2 клас) учитель дає таку інструкцію: «Спочатку один учень з пари іншому уголос читає перший абзац тексту (їх у цьому тексті — чотири), а потім коротко переказує зміст прочитаного, починаючи речення словами: «У цьому абзаці йдеться про те, що...». Потім другий учень ставить першому запитання щодо цього фрагменту, а той відповідає» [1, с.106].

Перша пара (для зразка) виконує завдання вголос. Далі учні читають самостійно, напівголосно, міняючись ролями на кожен абзац. Учитель контролює та коректує порядок роботи. Потім педагог пропонує озвучити для всіх сформульовані запитання.

Ефективним у роботі з текстом є «Спрямоване читання», яке передбачає самостійне читання, постановку запитання та обговорення змісту [2]. Перш ніж виконувати цю вправу, вчителю необхідно розбити текст на частини, які учні будуть читати мовчки. До кожної частини тексту педагог готує одне або два запитання, на які немає у змісті готової відповіді.

Детальніше розглянемо технологію на прикладі легенди «Вавилонська вежа» (4 клас):

Учитель. Зараз ви будете мовчки читати легенду «Вавилонська вежа», роблячи час від часу зупинки. Перед кожною частиною твору я ставитиму вам запитання, а ви будете читати твір та знаходити на нього відповідь. Слухайте уважно, у яких місцях тексту треба переривати читання.

Учитель. Прочитайте, будь ласка, перші чотири абзаци та знайдіть відповідь на запитання; Що допомогло людям домовитися про будівництво вежі? З яким настроєм вони почали працювати?

(Учні мовчки читають перші чотири абзаци легенди. Через кілька хвилин учитель повторює свої запитання, а діти дають на них відповіді.)

Учитель. Прочитайте вголос речення, де про все це говориться.

(Учні читають слова на підтвердження своєї думки.)

Учитель. А зараз ми прочитаємо наступні два абзаци та дізнаємось яким ви уявляєте місто Вавилон, що виросло навколо гори. Будьте готові підтвердити свої уявлення реченнями з тексту [3, с.69].

(Школярі мовчки читають наступні два абзаци легенди. Педагог повторює запитання, а учні дають на нього відповіді.)

Учитель. А тепер прочитайте наступний уривок тексту до слів «малярі пензлі занурюють у відра із синьою фарбою» та з’ясуйте, чому для верхньої частини вежі будівельники використали синій і золотавий кольори?

(Учні мовчки читають наступний уривок легенди і дають відповідь на запитання.)

Учитель. Прочитайте наступні два абзаци і з’ясуйте, чому Бог Ягве наслав на землю страшенну бурю?

(Педагог повторює запитання, а учні дають на нього відповіді та читають слова на підтвердження своєї думки.)

Учитель. Прочитайте, будь ласка, наступний уривок до слів «.хто б міг їх зрозуміти?» і дайте відповідь на таке запитання: Чому після бурі люди перестали розуміти один одного?

(Учні мовчки читають наступний уривок легенди і дають відповідь на запитання.)

Учитель. Давайте дочитаємо оповідання і з’ясуємо, яку думку передають виділені слова.

Учні мовчки читають наступні два абзаци легенди, після чого педагог повторює запитання, а школярі дають на нього відповіді та читають слова на підтвердження своєї думки.

Учитель. Які людські риси примусили бога Ягве роз’єднати людей?

Після «Спрямованого читання» учитель пропонує дітям дискусійне запитання: Це добре чи погано, що існує багато мов?

Зазначена технологія вчить учнів розуміти текст, виділяти в ньому основні поняття, аргументувати власні думки, міркувати над прочитаним.

«Подумай, доведи, порівняй, відгадай, зроби висновок» — так доцільно відповідати на запитання учнів, прагнучи розвинути їхній інтерес до світу, їхню фантазію, думку [1, с.107].

Необхідно цілеспрямовано виробляти у школярів уміння помічати у предметі яскраве, характерне й зображувати його словом, виховувати внутрішню потребу передавати власне бачення світу, власне сприймання краси.

Завдяки органічній взаємодії слова й унаочнення діти вчаться висловлювати свою думку. Вправляння у спостережливості, спогляданні предметів, виділенні їх ознак є кращим способом, за допомогою якого можна досягти самостійності, розвиваючи дар слова.

Саме тому, при вивченні рідної мови учнями варто пропонувати їм завдання на основі місцевого матеріалу, який сприяє розвитку пізнавальної активності у ході навчання.  Ось приклади таких завдань.

Тема 1. Звуки мови. Букви. Алфавіт.

• Запишіть до перших десяти букв алфавіту імена людей, з якими ви особисто знайомі, або запам’ятали з оповідання, казки, кінофільму. (а – Алла, б – Богдан і т.д.).
• Запишіть прізвища відомих людей нашого села, району або всієї держави які ви знаєте.
• Запишіть в алфавітному порядку назви: рослин, що ростуть на городі, (в саду, на клумбі), підкресліть букви, що позначають два звуки (я, ю, є, ї); тварин, які є у вас вдома, підкресліть слова з м’яким знаком;  птахів нашої місцевості, підкресліть слова з м’якими приголосними;  транспорту, який є в селі і в районі [3, с.69].

Тема 2. Склади. Перенос слів.

• Запишіть двоскладові слова – назви навчального приладдя. Поділіть рискою для переносу лише ті, в яких наголошений перший склад.
• Пригадайте трискладові слова – назви предметів, які потрібні на уроках трудового навчання (малювання). Запишіть їх, поділіть для переносу.
• Без яких предметів не можна обійтися при приготуванні їжі. Запишіть їх назви, поділіть для переносу.

Тема 3. Слова – назви предметів (Іменники)

• Які овочі ви вирощуєте з мамою на городі? Напишіть лише ті назви які мають літеру?
• Які дерева (кущі, квіти) ростуть у вашому саду?
• Що ви можете купити в місцевому продуктовому магазині? Запишіть їх назви і поставте наголос.
• Що продають в меблевому магазині. Запишіть назви і визначне кількість складів. Підкресліть слова, до яких можна поставити слово моя.
• Які установи є на центральній вулиці нашого села. Запишіть їх назви, визначте кількість звуків.
• Запишіть слова – назви овочів (фруктів, ягід) за першими буквами алфавіту (або на вибір). (Наприклад, А – абрикос, аґрус, айва, алича, апельсин, ананас...). Які з них ростуть у нашій місцевості.
• Вкажіть професії, назви яких мають букву с. Яка з них вам найбільше подобається. Складіть речення з цим словом [4, с.5].

Тема 4. Велика буква. Власні іменники.

• Згадайте письменників, твори яких читали. Запишіть їх прізвища в алфавітному порядку.
• Назвіть прізвище свого улюбленого письменника. Про кого він пише у свої творах. Які імена вам запам’яталися. Запишіть їх.
• Запишіть в алфавітному порядку прізвища учнів нашого класу з буквою а. Підкресліть трискладові слова.
• Які вулиці нашого села ви знаєте? Запишіть їх. Чому вони так називаються?
• Запишіть назви сіл, міст нашого району. Які знаєте. У яких селах, містах ви бували? Складіть і запишіть про це кілька речень.

Тема 5. Слово – назви ознак (Прикметники)

• Назвіть слова – ознаки предметів, які ви можете побачити в шкільній бібліотеці. Запишіть їх разом з словами, назвами предметів.
• Доберіть назви взуття до деяких ознак (спортивні, великі, гарні, малесенькі, зручні, тісні).
• До назв дерев, що ростуть біля нашої школи, доберіть ознаки, введіть ці слова в речення.
• Опишіть свою вулицю, річку, сад, вживаючи ознаки предметів за розміром, кольором, матеріалом.

Тема 6. Слова – назви дій. (Дієслова)

• Запишіть слова – назви дій, які ми виконуємо на уроці фізкультури, читання, математики, малювання. Побудуйте речення за схемою
• Запишіть слова – назви дій, які виконують у полі, на фермі, будівництві. Які дії ви спостерігали особисто? Запишіть 2-3 речення. Слова – назви дій підкресліть.
• Що робить учитель у школі (лікар у лікарні, фермер у полі)? Які дії ви спостерігали особисто? Запишіть речення.
• Доберіть слова – назви дій до теми “Весняна сівба”, “Навчання в школі”, “Будується будинок” [1, с.108].

Ми бачимо, що в наш час змінюються пріоритети цілей навчання. На перший план висувається його розвиваюча функція, культ самостійності і нестандартності думки, який стимулює розвиток пізнавальної активності дітей.

Стародавня китайка приказка стверджує: “Я слухаю – і я забуваю, я бачу – і я запам’ятовую, я роблю – і я розумію”.

Сьогодні у школі в основному реалізується перше, дуже мало другого, на жаль майже відсутнє третє.

В навчанні цінна не лише сама істина, але й сам процес її здобування, пошуку, спроби, помилки, усвідомлення прийомів розумової роботи – тобто все, що розвиває творчу думку школяра, привчає їх мислити і діяти самостійно.

Активність думки вчитель збуджує тим, що створює умови для дозріван-ня думки. Найперші помічники для вчителя у цьому добре сформульовані пізнавальні завдання на доведення судження вчителя, власної думки учня.

Необхідно навчити дітей розрізняти поняття “Причина” і “наслідок”. Причина – це те явище, яке призвело до іншого, наступного за ним; наслідок – явище, яке виникло через причину [3, с.69].

Дуже важливим є стимулювання пізнавальної діяльності учнів на уроках математики. Пріоритетним напрямом у моїй роботі є розвиток логічного мислення й математичного мовлення. В різній методичній літературі описано чимало засобів і прийомів. Треба намагатися використовувати їх комплексно, щоб уникнути монотонного й одноманітного розв’язування вправ і задач, яке може викликати в учнів відразу до предмета [4, с.5].

Для вдосконалення обчислювальних навичок підбирати цікавий і пов’язаний з життям матеріал.

Наприклад:

За день з погано закритого крана витікає 14 л води. У школі 25 кранів. Скільки води може витекти з усіх цих кранів? Як позбутися втрат води?

Ліс росте довго. Посаджені сьогодні дерева стануть великими лише тоді, коли підростуть онуки тих, хто їх саджав. Зрізати джерела можна буде через 85-95 років. У яких роках це буде?

Міцні знання, уміння й навички учні набувають у процесі активної пізнавальної діяльності, важливим збудником якої є інтерес. Щоб підтримати цей інтерес використовую різні форми зацікавленості: дидактичні і сюжетні ігри, задачі у віршах, задачі-жарти, ребуси, ігрові і цікаві ситуації. Не менш корисні вправи із серії “Цікава математика”, “У царстві геометричних фігур”, в яких передбачається оригінальне розв’язування нестандартних задач, вибір раціональних способів дослідження, порівняння, доведення. Вони потребують від кожного учня вищого ступеня творчої активності, гнучкості мислення [6, с.71].

Отже, розглянуті стратегії сприятимуть формуванню в молодших школярів мовно-мовленнєвої та літературознавчої компетенції, умінь мислити критично, самостійно знаходити, вивчати й аналізувати інформацію, мислити мобільно, аргументовано відстоювати власну точку зору, бути відкритим для сприйняття думок інших людей; помічати помилкові судження інших, своєчасно виправляти власні помилки, адекватно оцінювати свої знання та сприймати зауваження вчителя й однокласників щодо допущених помилок і недоліків.

     2.2. Методичні рекомендації щодо формування у дітей критичного мислення

Критичне мислення — мислення самостійне. Учні повинні мати достатньо свободи, щоб мислити й самостійно вирішувати найскладніші питання. Мислити критично можна в будь-якому віці. Навіть у першокласників накопичено для цього достатньо життєвого досвіду та знань. Навіть малюки здатні думати критично й самостійно. Саме завдяки критич­ному мисленню традиційний процес пізнання стає свідомим, неперервним та продуктивним [4, с.5].

Критичне мислення передбачає обов'язкову присутність етапу перевірки та оцінки припущень перед відповіддю на поставлене питання з точки зору їх достовірності і значущості, на противагу оперування готовими фразами, підказаними пам'яттю, без участі їх творчої переробки [6, с.71].

Дослідницькі навички, що їх використовують у критичному мисленні:

• Спостерігати - бачити і помічати властивості об'єкта.
• Описувати - зазначати, як об'єкт виглядає.
• Порівнювати - встановлювати подібності й розбіжності між об'єктами; оцінювати що-небудь і порівнювати з іншими речами.
• Визначати - показувати чи доводити існування об'єкта; розпізнавати об'єкт як конкретну річ.
• Асоціювати - розумово установлювати зв'язок між об'єктами; з'єднувати об'єкти за принципом їхньої взаємодії.
• Узагальнювати - робити висновки на основі наявної інформації чи фактів.
• Прогнозувати - передбачати, що відбудеться в майбутньому; пророкувати що-небудь.
• Застосовувати - використовувати у відповідності; отримувати практичну користь від чого-небудь [4, с.6].

Для того щоб учні могли скористатися своїми можливостями критичних мислителів, важливо, щоб вчитель розвивав у них низку важливих якостей, серед яких:

1. Готовність до планування. Оскільки думки часто виникають хаотично, важливо упорядкувати їх, вирішити, у якій послідовності їх викласти. Упорядкованість думки - ознака впевненості.
2. Гнучкість. Якщо учень не готовий сприймати ідеї інших, він ніколи сам не зможе стати генератором ідей. Гнучкість дозволяє почекати з винесенням судження, поки учень не буде мати різноманітну інформацію.
3. Наполегливість. Часто, зіштовхуючись з важкою задачею, учні вирішують відкласти її розв'язання на невизначений час. Вчителю слід виробляти наполегливість у напруженні розумових сил, тоді учні обов'язково досягнуть значно ліпших результатів навчання.
4. Готовність виправляти свої помилки. Людина, що критично мислить, намагатиметься не виправдати свої неправильні рішення, а зробити правильні для себе висновки, скористатися помилкою для продовження навчання.
5. Усвідомлення. Це дуже важлива якість, що передбачає уміння спостерігати за собою в процесі розумової діяльності, відслідковувати перебіг міркувань.
6. Пошук компромісних рішень. Важливо, щоб ухвалені рішення могли сприйняти інші люди, інакше ці рішення так і залишаться на рівні висловлювань [4, с.7].

Критичне мислення є досить складним процесом творчої переробки інформації, пов’язаної з її усвідомленням, переосмисленням такої діяльності.

Працюючи з розвитку критичного мислення, потрібно усвідомлювати, що навчити учнів мислити критично з першого уроку фактично неможливо. Критичне мислення формується поступово, воно є результатом щоденної кропіткої роботи вчителя й учня, з уроку в урок, з року в рік. Не можна виділити чіткий алгоритм дій учителя з формування критичного мислення в учнів. Але можна виділити певні умови, які представлені на рис.2.1., створення яких здатне спонукати і стимулювати учнів до критичного мислення [6, с.72].

Рис.2.1.

Критичне мислення формується та розвивається під час опрацювання інформації, розв’язання задач, проблем, оцінки ситуації, вибору раціональних способів діяльності. Тому такі уроки, на яких це постійно відбувається, створюють плідні умови для формування та розвитку критичного мислення. Якщо ж планувати етапи уроку з використанням на них відповідних форм та методів формування та розвитку критичного мислення, то результат буде ще більш високим [4, с.8].

ВИСНОВКИ

Одним з основних завдань системи освіти України є підготовка громадян здатних критично мислити. Ключова роль критичного мислення у розвитку сучасної особистості спричинена динамічністю соціальних систем та зростання обсягів інформації, необхідністю критично аналізувати її.

Нині у навчанні переважає не механічне передавання і засвоєння знань, а діяльність, що сприяє розвиткові учнів. У розвивальному навчанні принципи, методи і прийоми навчання спрямовані на досягнення найбільшої ефективності розвитку пізнавальних можливостей школярів: сприймання, мислення, уяви, пам’яті тощо. Спираючись на незавершені цикли психічного розвитку дитини, розвивальне навчання формує мислительні здібності, самостійність школярів, інтерес до навчання, а також удосконалює різні форми сприймання. Методика розвивального навчання передбачає інтенсивну розумову роботу учнів, що сприяє розвитку їх мислення.

Головними педагогічними чинниками розвитку критичного мислення учнів на уроках у початкових класах є такі: час, очікування ідей, вільне спілкування, повага до думки інших, віра у свої сили, активна життєва позиція.

Використання елементів технології розвитку критичного мислення учнів початкових класів на уроках має ґрунтуватися на системі психолого-педагогічних та дидактичних умов, серед яких:

• урахування індивідуальних та вікових особливостей учнів у способах організації їх діяльності на уроках;
• гармонізація емоційного й інтелектуального факторів навчання;
• проблематизація змісту навчального матеріалу;
• забезпечення взаємозв’язку урочної та позаурочної роботи  у початкових класах.

Отже, критичне мислення формується внаслідок добре організованого навчального процесу. З метою розвитку критичного мислення учнів необхідно особливу увагу звернути також на усвідомлення учнями того, як проходять їх мислительні операції, на застосування закономірностей теорії поетапного формування розумових дій, демонстрування учням структури і способу мислення, спілкування учнів між собою та з учителем у процесі роботи. Це дозволить учням послідовно підійти до усвідомленого формування відповідних умінь критичного мислення та їх застосування на практиці. Навчання критичному мисленню приводить учнів до чіткого розуміння того, що отримані результати залежать від способу їх отримання.

                                       СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ:

1. Богданович M.B. Методика викладання математики в початкових класах / M.B.Богданович, M.B.Козак, Я.А.Король. -Тернопіль: Навч. книга - Богдан, 2001. - 368 с.
2. БраусДж. А., Вуд. Инвайронментальноеобразование в школах [Текст] / Дж.А.Браус, Д.Вуд / Пер. с англ. NAAEE. — М., 1994.
3. Брушлинский А.В. Психологиямышления и кибернетика / А.В.Бруш-линский. - М.: Наука, 1970. - 220 с.
4. Ганин Е.А. Педагогическиеусловияиспользованиясовременныхинформационных и коммуникационныхтехнологий для самообразова-ниябудущихучителей [Электронный ресурс] / Е.А.Ганин // Информационныетехнологии и образование. - 2003. - № 13. - Режим доступа: http://ito.edu.ru/2003/VII/VII-0-1673.html
5. Гончаренко С. Український педагогічний словник / С.Гончаренко. - К.: Либідь, 1997. - 376 с.
6. Державний стандарт початкової загальної освіти [Текст] // Початкова школа. — 2011. — № 7. — С.1-18.
7. Концепція Нової української школи [Електронний ресурс].— Режим доступу: https://www.kmu.gov.ua/storage/app/media/reforms/ ukrainska-shkola-compressed.pdf
8. Красовицький М. Проблеми виховання критичного мислення учнів у контексті теорії і практики американської школи / М.Красовицький, О.Белкіна // Рідна школа. - 2003. - №2. - С.73-76.
9. Кроуфорд А. Технології розвитку критичного мислення учнів / А.Кроуфорд, В.Саул, С.Метьюз, Д.Макінстер / [наук. ред., передм. О.І.Пометун]. - К.: Вид-во «Плеяди», 2006. - 220 с.
10. Марченко О.Г. Формування критичного мислення школярів / О.Г.Марченко. - Харків: Вид. група «Основа»: «Тріада +», 2007. - 160 с.
11. Математика. Програма для загальноосвітніх навчальних закладів. 1-4 класи [Текст] / О.В.Онопрієнко, С.О.Скворцова, Н.П.Листопад // Навчальні програми для загальноосвітніх навчальних закладів із навчанням українською мовою. 1-4 класи. — К.: Видавничий дім «Освіта», 2011. — С.138-170.
12. Осинская В.М. Формирование умственной культуры учащихся в процессе обучения математике / В.М.Осинская. - К.: Рад. школа, 1989. - 192 с.
13. Психология. Учебное пособие / Под ред. В.А.Крутецкого. - М.: Просвещение, 1974. - 304 с.
14. Свечников А.А. Решение математических задач в 1-3 классах / А.А.Свечников. - М.: Просвещение, 1986. - 160 с.
15. Скворцова  С.О. Математика. 4 клас: підруч. для 4 кл. загальноосвіт. навч. закл.: у 2 ч. — Ч. 1 / С.О.Скворцова, О.В.Онопрієнко. — Х.: Видавництво «Ранок», 2015. — 144 с.
16. Скворцова  С.О. Методична система навчання розв'язування сюжетних задач учнів початкових класів: монографія / С.О.Скворцова. — Одеса: Астропринт, 2006. — 696 с.
17. Сорина  Г.В. Критическое мышление : История и современный статус / Г.В.Сорина // Вестник Московского университета. Серия 7. Философия. - 2003. - № 6. - С.97-110.
18. Сухомлинский В.А Сто советов учителю / В.А.Сухомлинский - К., - 1984 - 254 с.
19. Сухомлинський В.О. Павлишська середня школа / В.О.Сухомлинський. - Твори. - К., 1977. - Т.4.
20. Темпл Ч. Критическое мышление - углубленная методика. Пос. 4. [Текст] / Ч.Темпл, Дж.Л.Стил, К.С.Мередит. — М.: Изд-во Ин-та «Открытое общество», 1998.