КУРСОВА РОБОТА Тема роботи: Реологічні властивості дисперсних систем

Військовий інститут танкових військ

Національного технічного університету

‘‘Харківський політехнічний інститут’’

 

 

 

Кафедра хімії та бойових токсичних хімічних речовин

 

 

 

КУРСОВА РОБОТА

Тема роботи: Реологічні властивості дисперсних систем

 

 

 

 

 

 

 

Виконав:

старший солдат         Владислав БЕВЗ

Керівник:

працівник ЗСУ               Оксана ТИЧИНА

 

 

 

 

 

 

Харків – 2020

ЗМІСТ

 

ВСТУП …………………………………………………………………………		3
1.	РЕОЛОГІЯ…………………………………………….…………………………...	6
	1.1 Загальна характеристика явища реологія ..………...………………	6
	1.2 Фундаментальні закони реології ….. ………………………………	7
2.	ТИПИ РІДИН ……………………………………………………………...	19
	2.1 Ньютонівські рідини...………………………………………………..	21
	2.2 Загальна характеристика неньютонівських рідин………………..	22
	2.3 Неньютонівські рідини з реологічними характеристиками, що не залежать від часу ………………………………………………………..	23
	2.4 Неньютонівські рідини з реологічними характеристиками, що залежать від часу ………………………………………………………..	27
3.	В’ЯЗКІСТЬ ДИСПЕРСНИХ СИСТЕМ	28
ВИСНОВКИ …………………………………………………………………..		32
ПЕРЕЛІК ПОСИЛАНЬ ………………………………………………………		33

ВСТУП

 

Реологія – наука про деформацію й текучість різних тіл. Предметом реології є дослідження різних видів деформації залежно від напруг. Механічні властивості реальних тіл характеризуються міцністю, пружністю, пластичністю, в’язкістю, липкістю (адгезією). Зазначені властивості залежать не тільки від хімічного складу матеріалу, а й від будови або структури.

Особливість цих речовин, як і дисперсних систем, полягає в тому, що в ході дослідження й виробництва необхідно враховувати нелінійність рівнянь, що пов’язують деформації й швидкості деформацій із напругами.

Широке застосування методів реології в багатьох галузях промисловості обумовлено двома основними причинами:

- фізико-механічні константи речовини, що визначаються методами реології в абсолютних одиницях, дозволяють робити розрахунки різних випадків плину систем по трубах, спусках, ринвах, у робочих органах машин і т.д.;

- ці константи дозволяють робити висновки про якість певних продуктів або напівфабрикатів, тобто контролювати й регулювати технологічний процес.

Тому метою даної роботи визначено провести аналіз  літературних джерел щодо реологічних властивостей дисперсних систем, розглянути фундаментальні закони реології. Дослідити типи рідин, характеристику ньютонівських і неньютонівських рідин, а також поняття в’язкості дисперсних систем.

 

 

 

 

 

 

РЕФЕРАТ

 

Курсова робота містить: 33 сторінки та 2 джерела посилань.

Об’єкт дослідження – реологічні властивості.

Мета роботи – провести аналіз літературних джерел щодо реологічних властивостей дисперсних систем.

В курсовій роботі розглянуто фундаментальні закони реології. Основними є закони Гука, Ньютона, Сен- Венана–Кулона. Визначено поняття напруженості та деформації.

Показано класифікацію типів рідин, загальну характеристику ньютонівських і неньютонівських рідин, які залежать й не залежать від часу.

Також розглянуто сучасні поняття в’язкості дисперсних систем. Показано рівняння Ейнштейна, яке справедливо для розбавлених розчинів.

 

Ключові слова: РЕОЛОГІЯ, ДИСПЕРСНІ СИСТЕМИ, ТЕЧІЯ, РІДИНА, ДЕФОРМАЦІЯ, В’ЯЗКІСТЬ

 

 

Курсант 231 навчальної групи

Владислав БЕВЗ

 _____________________

                (підпис)

 

 

 

 

 

 

ABSTRACT

 

The course work contains: 33 pages and 2 source of links.

The object of research is rheological properties.

The purpose of the work is to conduct the analysis of literary sources in relation to rheologycal properties of the dispersible systems.

The fundamental laws of rheology are considered in the course work. Basic are laws of  Hooke’s, Newton’s Saint-Venant’s-Coulomb’s law. The concept of tension and deformation is certain.

Classification of types of liquids, general description of newtonian and non-newtonian liquids that depend and does not depend on time, is shown.

The modern concepts of viscidity of the dispersible systems are also considered. Equalization of Einstein, that justly for dilute solutions, is shown.

 

KEYWORDS: RHEOLOGY, DISPERSIBLE SYSTEMS, FLOW, LIQUID, DEFORMATION, VISCIDITY

 

Cadet of 231 study group

Vladyslav BEVS

_____________________

                (sign)

 

 

 

 

 

 

1. РЕОЛОГІЯ

 

1.1  Загальна характеристика явища реології

 

Реологія – наука про деформацію й текучість різних тіл. Предметом реології є дослідження різних видів деформації залежно від напруг. Механічні властивості реальних тіл характеризуються міцністю, пружністю, пластичністю, в’язкістю, липкістю (адгезією). Зазначені властивості залежать не тільки від хімічного складу матеріалу, а й від будови або структури. Отже, правильніше ці властивості називати структурно-механічними або реологічними, оскільки наука про деформацію й текучість даних тіл, явища релаксації й тиксотропії зветься реологією. Реологія є одним із розділів фізико-хімічної механіки. [2]

Під час реологічних досліджень систем ґрунтуються на:

- гіпотезі суцільного середовища, що деформується та характеризується мірою рухливості, величиною й швидкістю зсуву;

- гіпотезі безперервності розподілу основних фізичних властивостей і швидкостей деформацій.

З огляду на ці дві гіпотези в реології широко використовується апарат математичного аналізу, що застосовується до безперервних функцій.

Розвитку реології значною мірою сприяв розвиток колоїдної хімії у зв’язку з технікою обробки й одержання полімерів і високомолекулярних сполук.

Особливість цих речовин, як і дисперсних систем, полягає в тому, що в ході дослідження й виробництва необхідно враховувати нелінійність рівнянь, що пов’язують деформації й швидкості деформацій із напругами.

У цей час методи реології широко використовуються в техніці й розрахунках, ними користуються під час дослідження різних матеріалів: глинистих суспензій, консистентних мастил, друкувальних фарб, бітумів при різних температурах, торфу, харчових продуктів, будівельних матеріалів, розчинів желатини, мінеральних суспензій тощо. Реологія має багато спільного з галузями наук, що займаються вивченням текучості речовини, – фізичної хімії, молекулярної фізики, теорії пружності й пластичності, механіки полімерів, ґрунтів. Методика дослідження одних матеріалів удосконалюється й узагальнюється на підставі вивчення результатів експериментів, проведених з іншими матеріалами.

Широке застосування методів реології в багатьох галузях промисловості обумовлено двома основними причинами:

- фізико-механічні константи речовини, що визначаються методами реології в абсолютних одиницях, дозволяють робити розрахунки різних випадків плину систем по трубах, спусках, ринвах, у робочих органах машин і т.д.;

- ці константи дозволяють робити висновки про якість певних продуктів або напівфабрикатів, тобто контролювати й регулювати технологічний процес. За даними Скотт-Блера, за допомогою реологічних експериментальних порівнянь можна простіше й швидше визначити відповідність стандарту хімічного складу продукту, ніж за допомогою відповідних хімічних аналізів.

Реологію поділяють на теоретичну й експериментальну. Завданням теоретичної реології є встановлення зв’язку між змінами деформацій або швидкостей деформацій і зміною напруги. Завданням експериментальної реології є розробка методів і приладів для вимірювання реологічних величин та одержання експериментальних даних для різних матеріалів.

 

1.2 Фундаментальні закони реології

 

Деформація – це відносне зміщення точок системи під дією зовнішніх сил або температури, при якому не порушується її суцільність. Розрізняють два основних види деформації: стиснення (розтягнення) і зсув, а такі деформації, як крутіння та вигин, можна розглядати як комбінації цих основних видів. Деформація відбувається у часі.

Деформації можуть бути пружними (оборотними) і непружними (залишковими). У відповідності з цим тіла поділяються на пружні і пластичні.

Деформації, які зникають після того, як дія зовнішніх сил припиняється, називаються пружними. При пружній деформації структура тіла (а також його довжина, об’єм, форма), повністю відновлюється після зняття навантаження.

Непружні деформації не зникають після припинення дії сил,  що їх викликали, і супроводжуються необоротними змінами в системі, які називають залишковою деформацією. Залишкова деформація, при якій не відбувається руйнування тіла, є пластичною, а тіла – пластичними.

Мірою деформації є відносна деформація γ, яка дорівнює відношенню абсолютної деформації (зміщення) Δx до первинного значення величини х, що характеризує розміри або форму тіла. Наприклад, розтягнення характеризується відносним подовженням тіла Δl/l (x = l – довжина).

Механічне напруження Р, що викликає деформацію тіла, визначається відношенням величини пружної сили до площі, на яку вона діє. Одиницею напруження є Паскаль (Па).

Напруження називається нормальним, якщо сила спрямована перпендикулярно до поверхні, та тангенціальним (дотичним), якщо сила спрямована по дотичній до цієї поверхні. Їм відповідають основні види деформації – розтягнення (стиснення) і зсув.

При ізотропному (всебічному рівномірному) стисненні всі матеріальні тіла поводяться як ідеально пружні тіла – це перша аксіома реології. Іншими словами, ізотропне стиснення різних за своєю структурою тіл (твердих, рідких, газів) викликає в них тільки пружну деформацію, яка супроводжується зменшенням розмірів системи при збереженні її форми та збільшенням густини. При знятті навантаження відновлюються первинні параметри тіла. З цього випливає, що ізотропне стиснення не дозволяє виявити структурні відмінності тіл.

Згідно з другою аксіомою реології, будь-яка матеріальна система має всі реологічні властивості (пружність, в’язкість, пластичність, міцність). Ці властивості виявляються при деформації зсуву, кількісні характеристики якої є найбільш інформативними у реологічних дослідженнях щодо вивчення структури.

Характер і величина деформації залежать від властивостей матеріалу тіла, його форми та способу застосування зовнішніх сил.

Деформація пружних тіл описується законом Гука, який встановлює зв’язок між прикладеним напруженням Р і деформацією γ:

 

 

 

де Е – модуль пружності Юнга, що характеризує пружні властивості тіла (жорсткість); його розмірність – Н*м^–2, або Дж*м^–3.

При досягненні деякого значення напруження, званого межею пружності Р_к, закон Гука не виконується.

При  Р  >  Р_к  відбувається  або  руйнування  у  разі  крихких тіл (крива 1 рис. 1.1), або виникають залишкові деформації  (крива  2, рис.1.1) і встановлюється течія з постійною швидкістю при постійному напруженні Р_т, що відповідає межі текучості (вона характеризує міцність тіла).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

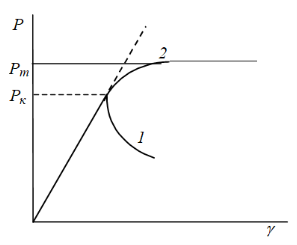
Рис. 1.1 – Діаграма напруження – деформація

 

Рідини та гази здатні текти (деформуватися) під дією дуже малих зовнішніх навантажень доти, поки вони діють, але в’язкість газів значно менша за в’язкість рідин. Так, в’язкість повітря при 20 ^оС становить 0,0181*10^–3 Па*с, води – 1*10^–3 Па*с, гліцерину – 1499*10^–3 Па*с,  а в’язкість твердих тіл може досягати 10¹⁵ – 10²⁰ Па*с. Така значна відмінність в’язкості твердих тіл від газових і рідких систем зумовлена особливостями їх структури. Завдяки цьому навіть при значних напруженнях зсуву в твердих тілах розвиваються лише пружні деформації.

Реологічні властивості рідини при зсуві характеризуються її в’язкістю η (при ламінарному режимі течії). Ламінарною (шаруватою) називають таку течію рідини, при якій частинки рідини рухаються вздовж прямолінійних траєкторій не перемішуючись. Іншими словами, рідина може бути представлена у вигляді сукупності шарів, які при течії ковзають один відносно одного (рис. 1.2). При русі шарів рідини з різними швидкостями між ними виникають сили внутрішнього тертя F_тер, або сили в’язкості.

 

 

 

 

 

 

 

 

 

 

 

 

 

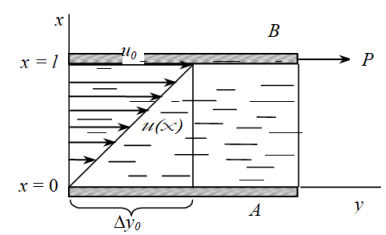
Рисунок 1.2 – Схема ламінарної течі

 

Течія ідеально в’язких тіл (рідин) описується законом Ньютона:

 

 

 

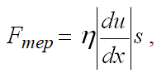
де |du/dx| – модуль градієнта швидкості в напрямі х, перпендикулярному напряму руху шарів; s – площа зіткнення шарів; η – коефіцієнт внутрішнього тертя, або динамічна в’язкість.

Фізичний зміст динамічної в’язкості полягає в наступному – вона чисельно дорівнює імпульсу, що переноситься від шару до шару за одиницю часу через одиничну площу при градієнті швидкості, рівному одиниці. Одиницею в’язкості в СІ є Паскаль*секунда [Па*с].

Якщо величина динамічної в’язкості характеризує опір рідини рухові, то величина υ = 1/η характеризує рухливість рідини і називається текучістю.

Вводячи в рівняння (1.2) напруження зсуву Р = F_тер/s і враховуючи, що градієнт швидкості течії при зсуві рівний швидкості деформації dγ/dt, прийдемо до співвідношення:

 

 

 

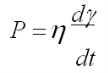
Рівняння 3 є також відображенням закону Ньютона, згідно з яким напруження зсуву визначає швидкість деформації.

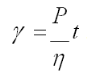Величина деформації рідини залежить від часу дії напруження, і можна показати, що деформація γ при постійному напруженні Р пропорційна часу дії t цього напруження:

 

 

 

Не менш важливу роль, ніж сили пружності і в’язкої течії, відіграють сили зовнішнього (або сухого) тертя (наприклад, при русі тіла, що знаходиться на площині, тертя постійне і не залежить від нормальної сили). Згідно з законом сухого тертя деформація відсутня, якщо напруження зсуву менше напруження сухого тертя, тобто, якщо виконується умова Р < Р_тер, то γ=0, dγ/dt = 0. При напруженні зсуву, що перевищує на нескінченно малу величину напруження сухого тертя, деформація та швидкість деформації можуть бути як завгодно великими (не мають обмежень). Тобто, якщо виконується умова Р = Р_тер, то γ > 0, dγ/dt > 0, і течія може відбуватися з будь-якою швидкістю. Ці висновки становлять суть закону Сен-Венана–Кулона і відображають реологічну поведінку ідеально пластичного тіла.

Трьом основним законам реології (закони Гука, Ньютона, Сен- Венана–Кулона) відповідають три елементарні моделі ідеальних реологічних властивостей матеріалів:

1) ідеально пружне тіло Гука – елементом пружних властивостей є пружина (рис.1.3а);

2) ідеально в’язке тіло Ньютона – елементом в’язкого тертя є опір поршня, зануреного в рідину (рис.1.3б);

3) ідеально пластичне тіло Сен-Венана–Кулона – елементом сухого тертя (ідеально пластичного тіла) є вантаж, який лежить на площині (рис.1.3в).

 

 

 

 

 

 

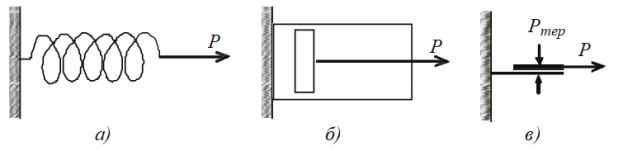
Рисунок 1.3 – Моделі ідеальних реологічних властивостей

 

Принципової відмінності в реологічних властивостях реальних рідких і твердих тіл немає, оскільки і ті, і другі являють собою конденсований стан речовини, який характеризується високою щільністю упаковки атомів і молекул і малою стисливістю. Також практично однакова природа сил міжмолекулярної взаємодії, які залежать тільки від відстані між частинками. Реологічні властивості реальних матеріалів поєднують в собі комбінації властивостей ідеально пружного і в’язкого тіла, а також елементи сухого тертя.

Відповідно до уявлень Максвелла, зміна механічних властивостей тіл у часі під дією навантажень можна розглядати як безперервний ряд переходів між ідеальним твердим тілом і рідиною, що дозволяє моделювати структурно-механічні властивості реальних тіл за допомогою ідеальних моделей.

Застосування простих ідеальних моделей для аналізу пружнопластично-в’язких властивостей реальних систем пов’язане з їх послідовним або паралельним з’єднанням. У першому випадку повне напруження Р припадає на кожний елемент, а повна деформація або її швидкість складаються з деформацій і швидкостей деформацій окремих елементів:

 

 

При паралельному з’єднанні елементів деформація і швидкість деформації окремих елементів однакові, а повне напруження складається з навантажень окремих елементів:

 

 

 

Так, Максвеллом на основі послідовного з’єднання елементів Гука і Ньютона була створена модель в’язко-пружної рідини (рис. 1.4). У цій моделі загальне навантаження передається повністю на елементи, тобто Р = Р_Г = Р_Н, а загальна деформація та її швидкість складаються з  відповідних   параметрів окремих  елементів, тобто γ = γ_Г + γ_Н.

 

 

 

 

 

 

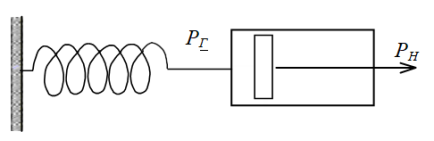
Рисунок 1.4 – Модель Максвелла

 

Виражаючи значення деформацій із рівнянь (1.1) і (1.4), отримаємо:

 

 

 

 

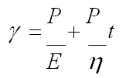
У цій моделі прикладення до системи постійного напруження Р призводить спочатку до пружної деформації тіла (γ = Р/Е), оскільки пружна деформація не вимагає для свого розвитку часу, а потім до рівномірного руху всієї моделі (згідно з рівнянням (1.3) dγ/dt=P/η), що визначається в’язким опором. Залежність деформації від часу описується рівнянням:

 

 

 

 

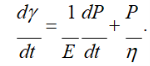
Рівняння (1.7, 1.8) є математичним виразом моделі Максвелла.

Після зняття напруження (Р = 0) система не повертається до вихідного стану, тобто деформація є необоротною.

Якщо в даній моделі миттєво викликати деформацію 0 і далі втримувати її постійною, то dγ/dt = 0, при цьому рівняння (1.8)

після поділення змінних приймає вид:

 

 

 

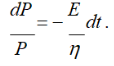
Інтегруючи (1.9) від Р₀ при t = 0 до Р при t, отримуємо

 

 

 

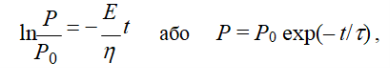
де τ = η/Е і визначає час релаксації напруження – час, протягом якого початкове напруження зменшується в е разів.

 Повна релаксація (відновлення) напруження, як випливає з (1.8), може наступити лише при t → ∞.

Час релаксації напруження, яке діє на систему, є одним з найважливіших параметрів фізико-хімічної механіки. Поведінка тіла визначається співвідношенням часу дії напруження та часу релаксації напруження. Наприклад, якщо τ значно більший за час дії напруження, то тіло називають твердим. У тому випадку, коли τ дуже малий у порівнянні з часом дії напруження, то тіло поводиться як рідина – напруження зменшується завдяки її течії.

Результатом паралельного з’єднання пружного елемента Гука і в’язкого елемента Ньютона є модель в’язкопружного твердого тіла (модель Кельвіна, рис. 1.5), для якої у відповідності з (1.1, 1.3, 1.6) справедливо:

 

 

 

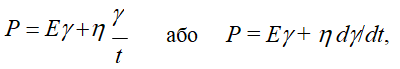
де dγ/dt – швидкість розвитку деформації. Ця модель відображає в’язкопружні властивості твердих тіл, здатних відновлювати свій первинний стан після зняття навантаження.

 

 

 

 

 

 

 

 

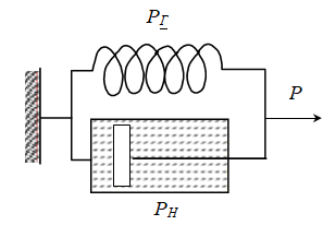
Рисунок 1.5 – Модель Кельвіна

 

Модель Кельвіна при умові дії на систему постійного напруження описується рівнянням:

 

 

 

 

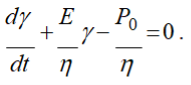
Після поділення змінних і інтегрування отримуємо:

 

 

 

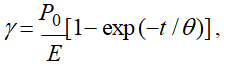
де θ = η/E – час релаксації деформації при постійному навантаженні, що характеризує еластичність тіла.

Деформація в такому тілі під дією постійного навантаження розвивається поступово. Якщо усунути деформуюче напруження, то пружні внутрішні напруження будуть прагнути повернути тіло у недеформований стан, а в’язкі сили будуть гальмувати цей процес, тобто система повертається у вихідний стан також протягом деякого часу. Залежність деформації від часу в моделі Кельвіна описується співвідношенням:

 

 

 

Повернення системи у вихідний стан після зняття напруження відбувається зі швидкістю, що зменшується. Процес уповільненої оборотної деформації називається пружною післядією, і здатність до нього визначає властивість еластичності; при цьому, чим більший час релаксації деформації, тим більша еластичність тіла.

Еластичні деформації, на відміну від пружних, мають ентропійний характер. Наприклад, еластична деформація полімеру призводить до менш імовірного розподілу конформацій молекул, що супроводжується зменшенням ентропії (ΔS < 0). Після зняття навантаження зразок полімеру самочинно скорочується, повертаючись до найбільш імовірного розподілу конформацій, тобто ентропія системи зростає (ΔS > 0).

При короткочасній дії сил реологічні властивості тіл Максвелла і Кельвіна обертаються: перше поводиться як пружний матеріал, а друге – як в’язка рідина. Це зумовлено тим, що за малий час у тілі Максвелла не встигають розвиватися залишкові деформації, пропорційні часу, а в тілі Кельвіна через малу величин у деформації внесок пружних сил у загальний опір стає неістотним.  [1]

 

 

 

 

 

 

2. ТИПИ РІДИН

 

Як відомо, усі рідини поділяють на ідеальні й реальні. Реальні рідини, у свою чергу, поділяють на ньютонівські й неньютонівські. Ньютонівські рідини підкоряються закону Ньютона. В’язкість ньютонівських рідин залежить від температури й тиску, але не залежить від швидкості зсуву і є фізичною властивістю рідини.

Неньютонівські рідини не підкоряються закону Ньютона, для них в’язкість – це параметр, що залежить не тільки від температури й тиску, а й від прикладеної напруги зсуву, тобто змінюється при зміні швидкості зсуву.

Неньютонівські рідини – це колоїдні суспензії й рідиноподібні речовини зі значними молекулярними масами, тобто рідиноподібні продукти, що належать до дисперсних систем. Вони мають просторову структуру, що під зовнішнім впливом здатна руйнуватися й відновлюватися. Неньютонівські рідини можна розподілити на три великі групи: стаціонарні системи, для яких співвідношення між швидкістю зсуву й напругою зсуву не залежить від часу; нестаціонарні системи, для яких зв’язок між напругою та швидкістю зсуву залежить від часу; системи, що мають властивості як твердого тіла, так і рідини й частково проявляють пружне відновлення форми після зняття напруги, так звані в’язкопружні рідини

 

2.1 Ньютонівські рідини

 

Оцінюючи властивості рідини, уводять поняття ідеальної й реальної рідин. Ідеальною рідиною називають рідину, що абсолютно не стискається під дією тиску, не змінює густини при зміні температури й не має в’язкості.

Реальні в’язкі рідини діляться на ньютонівські (підпорядковуються закону Ньютона) і не ньютонівські (структуровані) рідини.

Ньютонівське поводження властиве рідинам, у яких енергія в’язкісного тертя зумовлена зіткненням невеликих молекул. Усі гази, рідини й розчини з невеликою молекулярною масою потрапляють у цю категорію.

В’язкість ньютонівських рідин. Розглянемо тонкий шар грузлої рідини між двома паралельними пластинами, що знаходяться на відстані dh одна від одної. Одна пластина нерухома, а до іншої прикладене зусилля, що зрушує, F (рис. 2.1). У стаціонарних умовах зусилля F має врівноважуватися з боку рідини силою, обумовленою в’язкістю.

 

 

 

 

 

 

 

 

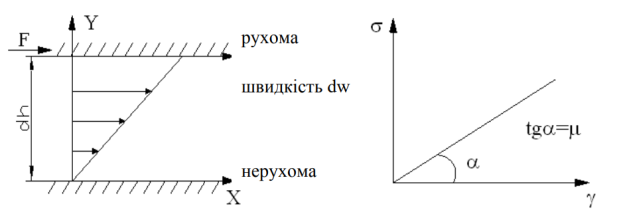
Рисунок 2.1 – Схема в’язкісного тертя

 

Ньютоном був установлений закон текучості в’язких рідин, для яких за умов ламінарного плину ньютонівської рідини напруга зсуву пропорційна градієнту швидкості, а величина в’язкості не залежить від швидкості деформацій, а саме:

 

 

 

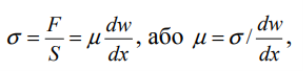
σ – величина напруги зсуву, н/м² (Па);

F – сила тертя, Н;

S – площа поверхні рухливої пластинки, м²;

µ – коефіцієнт в’язкості ньютонівської рідини, н*с/м², або Па*с;

γ = (dw/dx) – градієнт швидкості розвитку залишкової або пластичної деформації зсуву (швидкість зсуву), 1/с.

Ньютонівська динамічна в’язкість µ залежить тільки від температури та тиску й не залежить від швидкості зсуву γ. Графік залежності між напругою та швидкістю зсуву для ньютонівської рідини – так звана «крива плину» – являє собою пряму лінію, що виходить із початку координат із тангенсом кута нахилу µ (рис. 2.1).

За законом Ньютона випливає, що напруга, необхідна для одержання необоротної деформації, пропорційна відношенню змінних нескінченно малих величин: змінної за радіусом швидкості деформації dw до змінної величини ширини зазору (або радіуса труби) dx, через який тече рідина, а також її коефіцієнта в’язкості, що залежить від природи рідини.

В’язкість характеризує внутрішній опір рідини, що виникає в ній під час деформації плину. Визначимо її розмірність. Розмірність напруги нам уже відома. Розмірність градієнта швидкості деформації випливає із зазначеного вище відношення (dυ/dx). Вона виводиться зі співвідношення см/с/см, що дорівнює 1/с (або с⁻¹).

Неважко помітити, що розмірність коефіцієнта в’язкості має відповідати розмірності напруги (дин/см2 поділеної на градієнт швидкості 1/с, тобто помноженої на розмірність часу (с). Звідси видно, що розмірність в’язкості ( µ ) = дин/см*с.

Одиницю динамічної в’язкості називають пуазом на честь ученого Пуазейля, що вивів закон ламінарного плину рідин по трубах. Вона відповідає внутрішньому опору шару рідини під час дії на неї сили в одну дину на площу в один квадратний сантиметр і такої, що зсуває зазначену площу за одну секунду на один сантиметр. При цьому ставиться умова, що площа, яка зсувається, розташована на відстані одного сантиметра від іншої, нерухомої площі. У міжнародній системі одиниць розмірність динамічної в’язкості – Н*с/м² (Па*с).

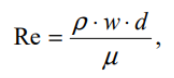Вимірюючи внутрішній опір плину або в’язкість рідин і рідиноподібних систем, варто дотримуватись ламінарності потоку, що виражається в розвитку деформацій зсуву лише строго паралельними шарами за відсутності завихрень у цих шарах (явища турбулентності). Характер деформації зсуву (режим плину) визначається безрозмірним параметром у вигляді критерію Рейнольдса (Re):

 

 

де ρ – густина рідини;

w – середня швидкість плину;

d – діаметр труби або ширина зазору;

µ – в’язкість ньютонівської рідини, істинна в’язкість.

Величина критерію Re для ламінарного потоку ньютонівських рідин не повинна перевищувати 2000–2500. Зі збільшенням в’язкості критерій зменшується. Для структур високої в’язкості критерій Рейнольдса знижується проти зазначеної величини більш ніж на один десятковий порядок. Якщо число Рейнольдса перевищує встановлену величину, то обчислення в’язкості за законами ламінарного плину втрачає сенс, оскільки для турбулентного, тобто вихрового, потоку закони ламінарного плину не виконуються. Об’єм рідини, що протікає крізь даний перетин труби при такій втраті напору, з турбулізацією потоку зменшується.

В’язкість рідин і розчинів низькомолекулярних сполук малої концентрації (ньютонівських рідин) визначається добре відомим законом Пуазейля:

 

 

 

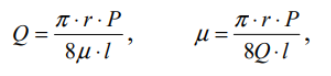
де Q – об’єм рідини, що протікає за одиницю часу;

l – довжина;

r – радіус труби, π =3,14;

Р – перепад тиску на довжині l.

В’язкість таких ньютонівських рідин постійна й не залежить від величини напруги σ або швидкості деформації зсуву γ = (dw/dx), що характеризується об’ємом рідини Q відносно межі, що визначається критерієм Рейнольдса. Її називають істинною в’язкістю.

2.2 Загальна характеристика неньютонівських рідин

 

Закону Ньютона про тертя всередині рідин не підкоряються концентровані розчини дисперсних колоїдних систем, що мають просторову структуру, рідиноподібні речовини зі значними молекулярними масами. Ці рідини помітно відрізняються від ньютонівських. До цієї групи належить більшість дисперсних продуктів харчових і кулінарних виробництв: молоко, кефір, кисляк, сметана, сир, креми, бульйони, розплавлений жир, м’ясний і ковбасний фарш, вершкове масло, маргарин, цукеркові маси, шоколад тощо. Ці дисперсні речовини, як правило, мають просторову структуру. До цієї категорії належать рідини, крива плину яких не є лінійною або не йде від початку координат, тобто динамічна в’язкість неньютонівських рідин не залишається постійною за заданих температур і тиску й залежить від інших чинників: швидкості деформації зсуву, конструктивної особливості апаратури, у якій перебуває рідина, передісторії рідини.

Зі зростанням напруги й швидкості деформації просторові структури подібних рідин руйнуються, в’язкість їх знижується. Це явище зветься аномалією в’язкості (її в таких випадках іноді називають структурною, уявною або ефективною в’язкістю).

Явище структурної в’язкості пояснюється тим, що в умовах більших швидкостей деформування дисперсної або високомолекулярної системи частина зв’язків структури, що руйнуються під час цього процесу, не встигає відновитися. Кількість таких зв’язків залежить від властивостей структури й швидкості її деформації. Після деякого витримування деформованої системи зруйновані зв’язки структури відновлюються, і вона набуває в’язкості, близької до тієї, що була в початковій, незруйнованій структурі. Так поводиться більшість структурованих систем під час деформування. Процес подальшого руйнування структури за постійної швидкості деформування й часткове відновлення зв’язків структури в часі зветься тиксотропією. Однак є й такі системи, що в межах відомих напруг і швидкостей деформацій не зменшують, а збільшують свою в’язкість. Це явище, що має назву «ділатенція», пояснюється розвитком під час деформування внутрішньої поверхні часток структури, що контактує з розчинником і знижує таким чином товщину шару молекул розчинника між частками.

Неньютонівські рідини з нелінійною кривою текучості можна розподілити на три великі групи:

а) системи, для яких швидкість зсуву в кожній точці становить деяку функцію напруги зсуву в цій же точці й не залежить від часу;

б) більш складні системи, у яких зв’язок між напругою й швидкістю зсуву залежить від часу й від передісторії рідини;

в) системи, що мають властивості як твердого тіла, так і рідини й частково виявляють пружне відновлення форми після зняття напруги (так звані в’язкопружні рідини).

 

2.3 Неньютонівські рідини з реологічними характеристиками, що не залежать від часу

 

Системи типу (а) можуть бути описані рівнянням γ = f (σ), з якого випливає, що швидкість зсуву в кожній краплі рідини є простою функцією напруги зсуву в тій же краплі. Такі речовини можуть бути названі не ньютонівськими рідинами. Їх зручно поділяти на чотири групи:

− бінгамівські пластичні рідини (бінгамівські пластики);

− псевдопластичні рідини (псевдопластики);

 – ділатантні рідини;

 – неідеально пластичні рідини.

На рис. 2.2 для порівняння подано графік лінійної залежності для ньютонівських рідин.

 

 

 

 

 

 

 

 

 

 

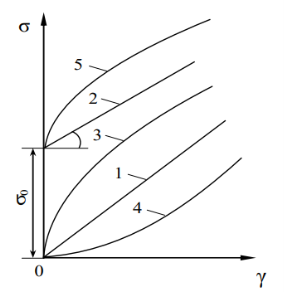
Рисунок 2.2 – Криві плину для п'яти груп рідин:

1 – ньютонівські; 2 – бінгамівські; 3 – псевдопластичні; 4 – ділатантні;

5 – неідеально пластичні

 

Бінгамівські пластики. Крива плину для цих матеріалів становить собою пряму лінію, що перетинає вісь напруги зсуву на відстані σ₀ від її початку. 

Напруга зсуву σ₀ є межею, перевищення якої призводить до виникнення в’язкого плину. Реологічне рівняння для бінгамівських пластиків можна записати в такому вигляді:

 

 

 

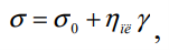
де η_пл – пластична в’язкість, що дорівнює тангенсу кута нахилу кривої плину; σ₀ – гранична напруга зсуву.

Це рівняння, що називається рівнянням Бінгама, характеризує ідеально пластичний плин рідини, за якого після перевищення межі плину (межі текучості) спостерігається пропорційність між швидкістю й напругою зсуву, тобто рідина поводиться як ньютонівська. Фізичне поводження таких матеріалів пояснюється їхньою структурою, що запобігає руху при напругах, менших за межу текучості.

Якщо , σ  > σ₀ то структура повністю руйнується, матеріал розпочинає зсувний плин і тече, як звичайна ньютонівська рідина. Прикладами систем, що підпорядковуються рівнянню Бінгама, можуть бути маргарин, шоколадні суміші, рідке мило й мийні засоби. Коли ж напруга зсуву стає меншою за σ 0, структура знову відновлюється.

Псевдопластики. Псевдопластичні рідини не виявляють межі текучості, тобто σ₀ = 0. Реологічне рівняння таких рідин, так зване рівняння Освальда де Віля, має вигляд

 

 

 

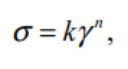
де k – міра консистенції рідини (чим вища в’язкість рідини, тим більше k);

n – ступінь неньютонівського поводження матеріалу, або індекс плину (чим більше n відрізняється від одиниці, тим чіткіше виявляються його неньютонівські властивості).

Виразимо в’язкість (ефективну або уявну) з рівняння Ньютона як

  

 

 

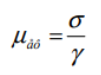
і, перетворивши формулу (3.5) з урахуванням цього виразу, одержимо:

 

 

 

Для псевдопластичних матеріалів n < 1, тому, аналізуючи рівняння (3.7) або рівняння Освальда, доходимо висновку, що ефективна в’язкість зменшується зі зростанням швидкості зсуву (рис. 2.3). Ця реологічна властивість пояснюється тим, що в нерухомому середовищі розташування асиметричних часток є хаотичним, а під впливом зростаючих зсувних сил частки або молекули починають поступово, своїми більшими осями, орієнтуватися вздовж напряму потоку.

 

 

 

 

 

 

 

Рисунок 2.3 – Повна реологічна крива

 

Унаслідок цього зі збільшенням швидкості зменшується взаємодія між частками і знижується сила тертя. Гадана в’язкість буде зменшуватися зі зростанням швидкості зсуву доти, поки зберігається можливість подальшого орієнтування часток уздовж ліній струму, а потім настає ньютонівський плин за умов постійної в’язкості. Псевдопластичний плин характерний для різних неньютонівських харчових матеріалів, зокрема томатних концентратів, цукрових розчинів, абрикосового пюре, хлібопекарського тіста, цукеркових мас, крохмальних суспензій, майонезу, мила тощо.

Ділатантні рідини. У ділатантних рідин також відсутня межа плинності, однак їх гадана або ефективна в’язкість підвищується зі зростанням швидкості зсуву. Степеневий закон кривої плину характеризується значенням n > 1. Такий плин є характерним для суспензій із більшим вмістом твердої фази. Ці суспензії в стані спокою мають мінімальний об’єм прошарків між твердими частками,  і рідини вистачає лише для заповнення цих прошарків. Коли такі матеріали піддаються зрушенню з невеликою швидкістю деформації, рідина є мастилом, що зменшує тертя часток одна об одну, і напруги, отже, невеликі. У разі більших зсувів щільне прилягання часток порушується, матеріал розбухає, тобто збільшується в об’ємі, і розміри рідких прошарків зростають. При новій структурі рідини недостатньо для змащення часток, що труться одна об одну, і діючі напруги в’язкісного тертя значно зростають. Процес структуроутворення і є причиною швидкого наростання ефективної в’язкості в разі збільшення швидкості зсуву.

Ділатантні матеріали в інженерній практиці використовуються значно рідше, ніж псевдопластичні. До таких рідин належать згущене молоко, деякі розчини кукурудзяного борошна, цукру, крохмалю, полімерний клей для сигарет, тощо.

 

2.4 Неньютонівські рідини з реологічними характеристиками, що залежать від часу

 

Багато реальних рідин не можуть бути описані простою реологічною залежністю. Ефективна в’язкість таких рідин визначається не тільки швидкістю зсуву, але і його тривалістю.

Тиксотропні рідини. Якщо тиксотропний матеріал, що перебуває в стані спокою, деформувати з постійною швидкістю зсуву (рис. 3.4), то його структура буде поступово руйнуватися, а ефективна в’язкість згодом зменшиться.

Реопектичні рідини. Для них властиве поступове структуроутворення під час зсуву, хоча для більшості рідин зсув сприяє руйнуванню структури. Розчин гіпсу твердішає після 40 хв вистоювання після струшування. Однак час затвердівання скорочується до 20 хв, якщо посудину з гіпсом обережно перекочувати. Для таких матеріалів невеликі переміщення зсувного характеру сприяють утворенню в’язкості, у той час як значні зсуви (струшування) руйнують її. Реопектичні рідини характеризуються тим, що під час плину поступово структура їх стає міцнішою, а в’язкість зростає. Для них також характерний прояв гістерезису на кривих плину. В’язкопружні рідини. Розглядають два загальних види деформації: оборотну (пружну), що зникає після припинення дії сили, і необоротну (в’язку і пластичну), що не зникає після зняття навантаження. [2]

 

3. В’ЯЗКІСТЬ ДИСПЕРСНИХ СИСТЕМ

 

Відмінність течії золів від течії звичайних індивідуальних рідин або істинних розчинів низькомолекулярних речовин зумовлюється тим, що в перших присутні у зваженому стані колоїдні частинки, розміри яких значно перевищують молекулярні розміри. Присутність таких частинок призводить до перемішування шарів рідини і виникнення турбулентності. Крім того, частинки дисперсної фази звужують простір, зайнятий самою рідиною у потоці, що зумовлює збільшення градієнта швидкості в напрямі, перпендикулярному потоку. Внаслідок цього в’язкість золів завжди вища за в’язкість дисперсійного середовища.

 Реологічні властивості розбавленої дисперсної системи, що містить тверді сферичні частинки, визначаються поведінкою окремих частинок у потоці. При зсуві шарів рідини сферична частинка переміщується поступально зі швидкістю, яка дорівнює швидкості потоку рідинного середовища, і крім того, залучається в обертальний рух. Розсіяння енергії внаслідок тертя поверхні частинки з середовищем зумовлене тільки цим обертальним рухом, оскільки у поступальному русі центр частинки нерухомий відносно потоку рідини в площині розташування центра. Таким чином, чим більше об’єм, що займає дисперсна фаза, тим більшим буде розсіяння енергії, а отже, тим вищою повинна бути в’язкість такої системи.

У найпростішому випадку, для порівняно розбавлених водних розчинів колоїдних ПАР, справедливе рівняння Ейнштейна:

 

 

 (XI.19)

де η – в’язкість колоїдного розчину, η₀ – в’язкість води при тій же температурі, φ – об’ємна частка дисперсної фази, α – коефіцієнт форми (для сферичних частинок α = 2,5). У концентрованих розчинах ПАР це рівняння вже непридатне; більше того, при збільшенні концентрації в'язкість зростає надзвичайно різко, і зрештою виникають рідкокристалічні і структуровані системи.

Вводячи поняття питомої в’язкості (η_пит), рівняння (3.1) можна представити у вигляді

 

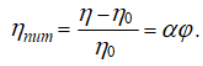
 (XI.20)

 

Рівняння (3.1, 3.2) виконуються при наступних умовах: система нестискувана, течія ламінарна, відсутні ковзання між частинками і рідиною і взаємодія між частинками. Із теорії Ейнштейна витікає, що в’язкість дисперсної системи з частинками, які не взаємодіють між собою, не залежить від їх розміру.

Рівняння Ейнштейна виправдовується тільки для ньютонівських рідин. Коефіцієнт  α для частинок несферичної форми, як правило, більший за 2,5. Для сильно анізодіаметричних частинок рівняння Ейнштейна непридатне. Це пояснюється тим, що при малих швидкостях зсуву такі частинки хаотично обертаються в рідині, при цьому значне число частинок може розташовуватися упоперек потоку, внаслідок чого в’язкість дисперсної системи у порівнянні з в'язкістю дисперсійного середовища значно підвищується. При великих швидкостях відбувається орієнтація частинок вздовж потоку і в’язкість системи зменшується. І в першому, і у другому випадках порушується ньютонівська поведінка рідини.

Рівняння Ейнштейна одержане в припущенні відсутності взаємодії між частинками дисперсної фази, тому воно справедливе для розбавлених розчинів.

Зі збільшенням концентрації дисперсної фази зростає взаємодія між частинками і спостерігаються відхилення від рівняння Ейнштейна (в’язкість у концентрованих системах зростає з концентрацією майже експоненціально), що зумовлено взаємодією частинок і, як наслідок, структуроутворенням. Такі системи відносяться до неньютонівських рідин. У найбільшій мірі це характерно для досить концентрованих систем, особливо тих, які містять паличкоподібні частинки. Окремі ділянки поверхні таких частинок позбавлені адсорбційних шарів або розвинених сольватних оболонок. Міжмолекулярна взаємодія на цих ділянках може спричинити злипання частинок, але більш повному контакту між частинками перешкоджають захисні шари на інших частинах поверхні. Наслідком такої взаємодії є утворення агрегатів, що містять в собі нерухому (імобілізовану) рідину. При малих швидкостях течії зчеплення між частинками встигає відновлюватися, і в’язкість системи виявляється значною. Висока швидкість потоку перешкоджає повному відновленню зв'язків між частинками, що призводить до зниження в’язкості. На реологічних кривих (рис. 3.1) для таких систем виявляються дві ділянки постійної в’язкості: 1 – відповідає незруйнованій структурі, 2 – повному її руйнуванню, між ними знаходиться ділянка змінної в’язкості, що відповідає різним ступеням руйнування структури.

 

 

 

 

 

 

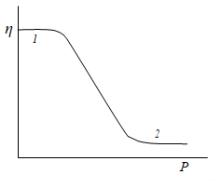
Рисунок 3.1 – Реологічна крива структурованої системи

Крім того, відхилення експериментально визначених значень  в’язкості від величин, знайдених за допомогою рівняння Ейнштейна, зумовлене сольватацією частинок. Сольватацією можна також пояснити і те, що в багатьох випадках спостерігається залежність в’язкості від  дисперсності системи при однаковій об’ємній концентрації дисперсної фази. Вплив сольватації можна пояснити таким чином. Ефективна об’ємна концентрація сольватованих частинок дисперсної фази φ і об’ємна концентрація частинок без сольватних оболонок φ₀ пов'язані співвідношенням

 

 

 (XI.21)

де δ і r – товщина сольватної оболонки і радіус частинки відповідно.

Із цього співвідношення слідує, що чим менші частинки дисперсної фази, тим більша їх ефективна об’ємна концентрація, а отже в’язкість повинна зростати зі зменшенням розміру частинок.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВКИ

 

В курсовій роботі розглянуто фундаментальні закони реології. Вказано, що трьом основним законам реології (закони Гука, Ньютона, Сен- Венана–Кулона) відповідають три елементарні моделі ідеальних реологічних властивостей матеріалів: ідеально пружне тіло Гука, ідеально в’язке тіло Ньютона та ідеально пластичне тіло.

Показано класифікацію типів рідин. Вказано, що ньютонівські рідини підкоряються закону Ньютона. В’язкість ньютонівських рідин залежить від температури й тиску, але не залежить від швидкості зсуву і є фізичною властивістю рідини. Неньютонівські рідини не підкоряються закону Ньютона, для них в’язкість – це параметр, що залежить не тільки від температури й тиску, а й від прикладеної напруги зсуву, тобто змінюється при зміні швидкості зсуву.

Розглянуто поняття в’язкості дисперсних систем. Показано, що реологічні властивості розбавленої дисперсної системи, що містить тверді сферичні частинки, визначаються поведінкою окремих частинок у потоці.

 

 

 

 

 

 

 

 

 

 

 

 

 

ПЕРЕЛІК ПОСИЛАНЬ

 

1.  Основы электрохимической термодинамики: учеб. пособие/ А.М. Мерецкий, В.В. Белик. – М.: РХТУ им. Д.И. Менделеева, 2011. – 180 с.

2. Реологія в процесах виробництва харчових продуктів : навч. посібник : у 2 ч. Ч. 1. Класифікація та характеристика неньютонівських рідин / [О. І. Черевко, В. М. Михайлов, В. І. Маяк, О. А. Маяк] ; Харк. держ. ун-т харчування та торгівлі. – Х. : ХДУХТ, 2014. – 244 с.