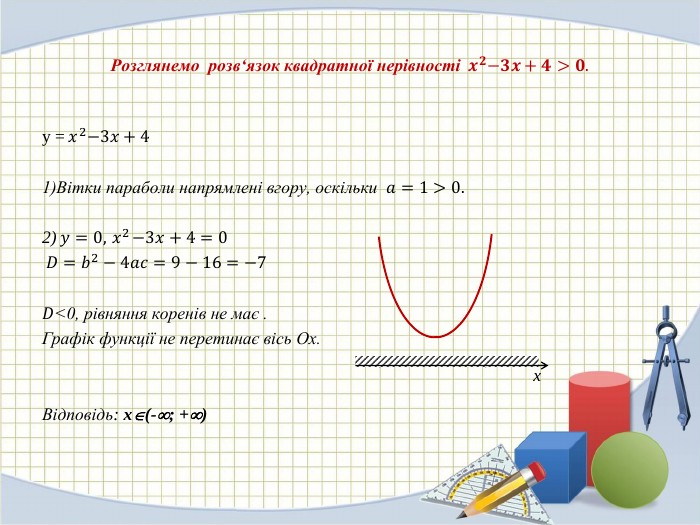
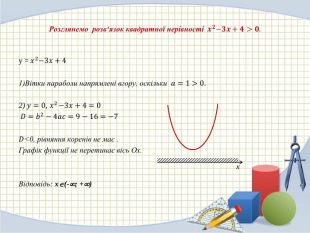
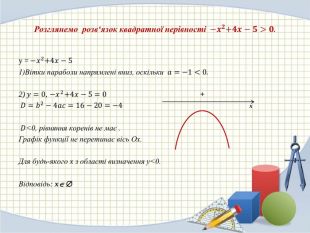
Квадратна нерівність. Графічний спосіб розв'язування квадратних нерівностей.
Про матеріал
Матеріал можна використовувати при організаціії дистанційного навчання, індивідуального навчання в закладах освіти. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку






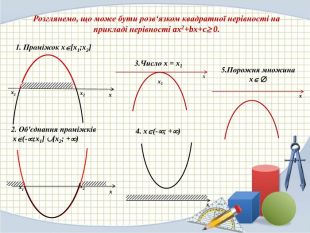
![xx1x2 Розглянемо, що може бути розв‘язком квадратної нерівності на прикладі нерівності ax2+bx+c 0.x2x11. Проміжок x[x1;x2]x1x5. Порожня множина x x4. x(-; +)x2. Об'єднання проміжків x(-;x1] [x2; +)x3. Число x = x1 xx1x2 Розглянемо, що може бути розв‘язком квадратної нерівності на прикладі нерівності ax2+bx+c 0.x2x11. Проміжок x[x1;x2]x1x5. Порожня множина x x4. x(-; +)x2. Об'єднання проміжків x(-;x1] [x2; +)x3. Число x = x1](/uploads/files/1804418/307586/334314_images/6.jpg)


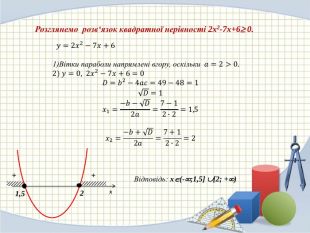
![Розглянемо розв‘язок квадратної нерівності 2x2-7x+6 0.1,5x 𝑦=2𝑥2−7𝑥+6 1)Вітки параболи напрямлені вгору, оскільки 𝑎=2>0. 2) 𝑦=0, 2𝑥2−7𝑥+6=0𝐷=𝑏2−4𝑎𝑐=49−48=1𝐷=1𝑥1=−𝑏−𝐷2𝑎=7−12∙2=1,5 𝑥2=−𝑏+𝐷2𝑎=7+12∙2=2 Відповідь: x(-;1,5] [2; +) 2++ Розглянемо розв‘язок квадратної нерівності 2x2-7x+6 0.1,5x 𝑦=2𝑥2−7𝑥+6 1)Вітки параболи напрямлені вгору, оскільки 𝑎=2>0. 2) 𝑦=0, 2𝑥2−7𝑥+6=0𝐷=𝑏2−4𝑎𝑐=49−48=1𝐷=1𝑥1=−𝑏−𝐷2𝑎=7−12∙2=1,5 𝑥2=−𝑏+𝐷2𝑎=7+12∙2=2 Відповідь: x(-;1,5] [2; +) 2++](/uploads/files/1804418/307586/334314_images/9.jpg)