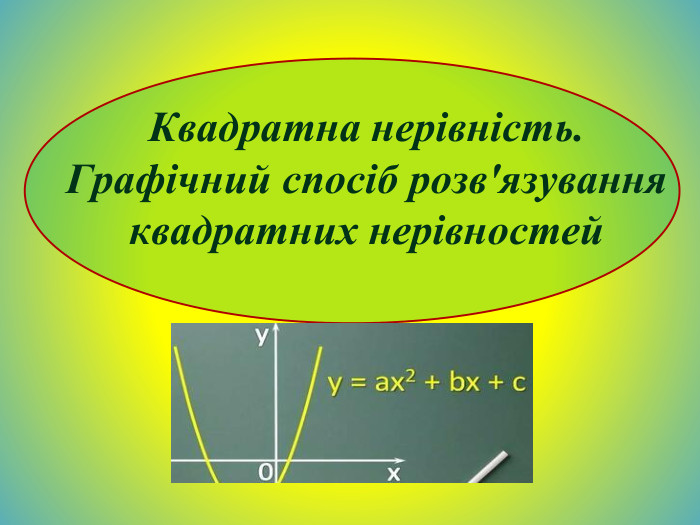
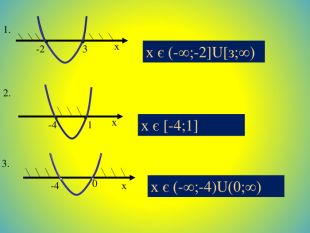Квадратна нерівність. Графічний спосіб розв'язування квадратних нерівностей










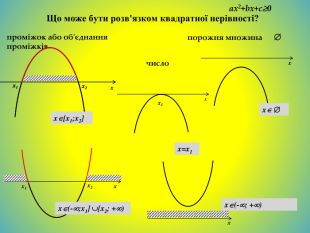
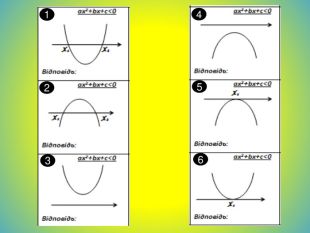
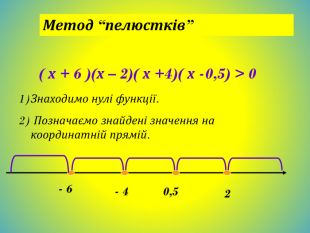
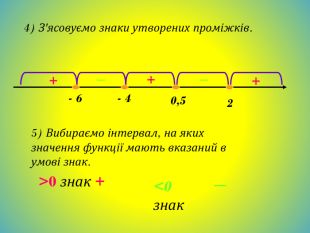
![Що може бути розв'язком квадратної нерівності?проміжок або об'єднання проміжківчислопорожня множина xx1x2xx1x2ax2+bx+c0xx2x1x[x1;x2]x(-;x1] [x2; +)x1x=x1xx xx(-; +)x Що може бути розв'язком квадратної нерівності?проміжок або об'єднання проміжківчислопорожня множина xx1x2xx1x2ax2+bx+c0xx2x1x[x1;x2]x(-;x1] [x2; +)x1x=x1xx xx(-; +)x](/uploads/files/36948/443679/504667_images/14.jpg)









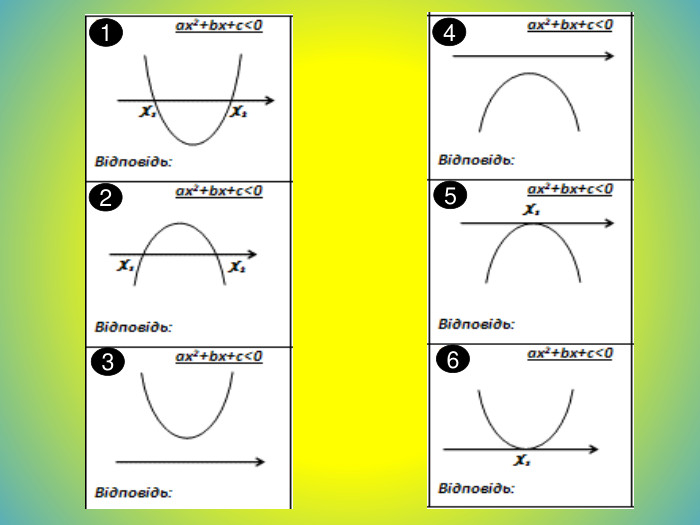



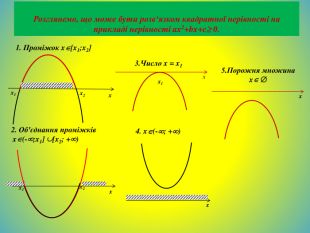
![xx1x2 Розглянемо, що може бути розв‘язком квадратної нерівності на прикладі нерівності ax2+bx+c 0.x2x11. Проміжок x[x1;x2]x1x5. Порожня множина x x4. x(-; +)x2. Об'єднання проміжків x(-;x1] [x2; +)x3. Число x = x1 xx1x2 Розглянемо, що може бути розв‘язком квадратної нерівності на прикладі нерівності ax2+bx+c 0.x2x11. Проміжок x[x1;x2]x1x5. Порожня множина x x4. x(-; +)x2. Об'єднання проміжків x(-;x1] [x2; +)x3. Число x = x1](/uploads/files/36948/443679/504667_images/37.jpg)
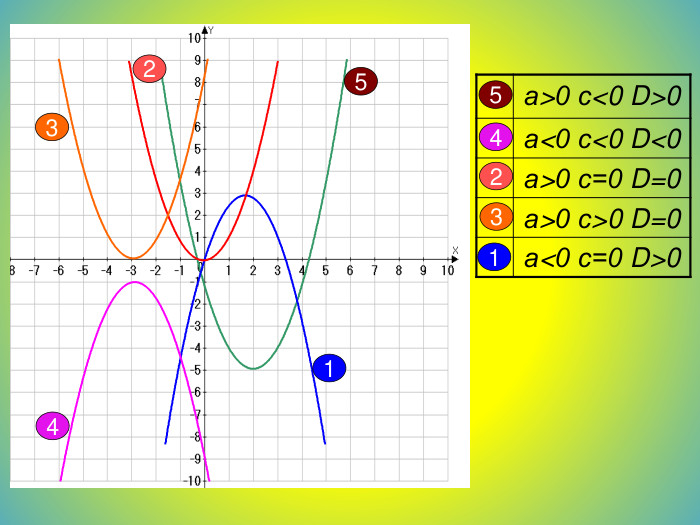






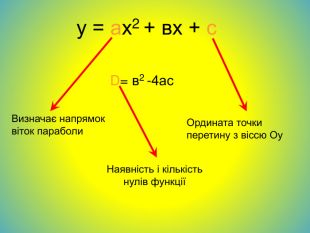
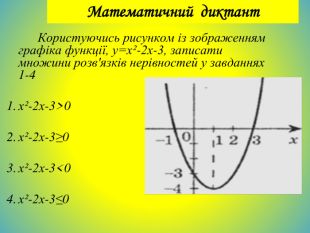
![Схема побудови квадратичної функціїПри побудові параболи користуються такими загальними формулами та властивостями квадратичної функції.1. Напрям віток параболи залежить від знака коефіцієнта a .а<0, вітки параболи напрямлені вниз.а>0 вітки параболи напрямлені вгору.2. Точки перетину параболи з осями координат є такими: Абсциса точки перетину параболи з віссю Oy дорівнює 0, тоді ,у(0)=с,(0;с) . Ордината точок перетину параболи з віссю Ox дорівнює 0, тоді, щоб знайти абсциси цих точок, треба розв’язати квадратне рівняння ах²+bx+c=0.3. Координати вершини параболи у=ах²+bx+c; Аналізуємо:1.)D(y); хєR(-∞;+∞) 2.)Е(у); ує [0;+∞) а>0 ує(-∞;0] а<0 3.)х=0; у=0 (0;0)-пер.3ох 3оу4.) Точки перетину графіка з осями координат. 5.)Зростання ;спадання6.)Найбільше,найменше значення функції min;max. Схема побудови квадратичної функціїПри побудові параболи користуються такими загальними формулами та властивостями квадратичної функції.1. Напрям віток параболи залежить від знака коефіцієнта a .а<0, вітки параболи напрямлені вниз.а>0 вітки параболи напрямлені вгору.2. Точки перетину параболи з осями координат є такими: Абсциса точки перетину параболи з віссю Oy дорівнює 0, тоді ,у(0)=с,(0;с) . Ордината точок перетину параболи з віссю Ox дорівнює 0, тоді, щоб знайти абсциси цих точок, треба розв’язати квадратне рівняння ах²+bx+c=0.3. Координати вершини параболи у=ах²+bx+c; Аналізуємо:1.)D(y); хєR(-∞;+∞) 2.)Е(у); ує [0;+∞) а>0 ує(-∞;0] а<0 3.)х=0; у=0 (0;0)-пер.3ох 3оу4.) Точки перетину графіка з осями координат. 5.)Зростання ;спадання6.)Найбільше,найменше значення функції min;max.](/uploads/files/36948/443679/504667_images/48.jpg)

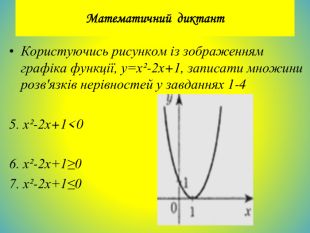
![Розглянемо розв‘язок квадратної нерівності 2x2-7x+6 0.1,5x 𝑦=2𝑥2−7𝑥+6 1)Вітки параболи напрямлені вгору, оскільки 𝑎=2>0. 2) 𝑦=0, 2𝑥2−7𝑥+6=0𝐷=𝑏2−4𝑎𝑐=49−48=1𝐷=1𝑥1=−𝑏−𝐷2𝑎=7−12∙2=1,5 𝑥2=−𝑏+𝐷2𝑎=7+12∙2=2 Відповідь: x(-;1,5] [2; +) 2++ Розглянемо розв‘язок квадратної нерівності 2x2-7x+6 0.1,5x 𝑦=2𝑥2−7𝑥+6 1)Вітки параболи напрямлені вгору, оскільки 𝑎=2>0. 2) 𝑦=0, 2𝑥2−7𝑥+6=0𝐷=𝑏2−4𝑎𝑐=49−48=1𝐷=1𝑥1=−𝑏−𝐷2𝑎=7−12∙2=1,5 𝑥2=−𝑏+𝐷2𝑎=7+12∙2=2 Відповідь: x(-;1,5] [2; +) 2++](/uploads/files/36948/443679/504667_images/50.jpg)















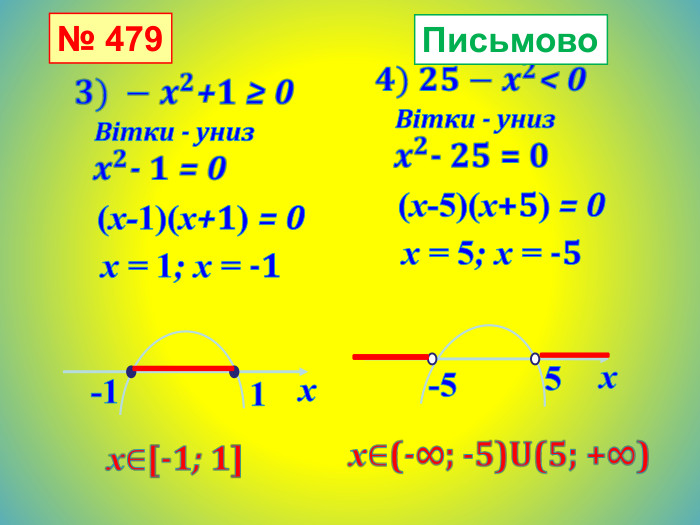
![1.х-23х є (-∞;-2]U[з;∞)2.-41хх є [-4;1]3.-40хх є (-∞;-4)U(0;∞) 1.х-23х є (-∞;-2]U[з;∞)2.-41хх є [-4;1]3.-40хх є (-∞;-4)U(0;∞)](/uploads/files/36948/443679/504667_images/73.jpg)
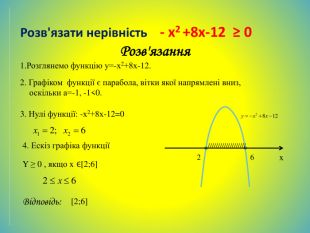
![1. Розглянемо функцію у=-х2+8х-12. 3. Нулі функції: -х2+8х-12=0 Відповідь:4. Ескіз графіка функції///////////////////2. Графіком функції є парабола, вітки якої напрямлені вниз, оскільки а=-1, -1<0. Y ≥ 0 , якщо x Є[2;6]x26[2;6]Розв'язати нерівність - x2 +8x-12 ≥ 0 Розв'язання 1. Розглянемо функцію у=-х2+8х-12. 3. Нулі функції: -х2+8х-12=0 Відповідь:4. Ескіз графіка функції///////////////////2. Графіком функції є парабола, вітки якої напрямлені вниз, оскільки а=-1, -1<0. Y ≥ 0 , якщо x Є[2;6]x26[2;6]Розв'язати нерівність - x2 +8x-12 ≥ 0 Розв'язання](/uploads/files/36948/443679/504667_images/74.jpg)







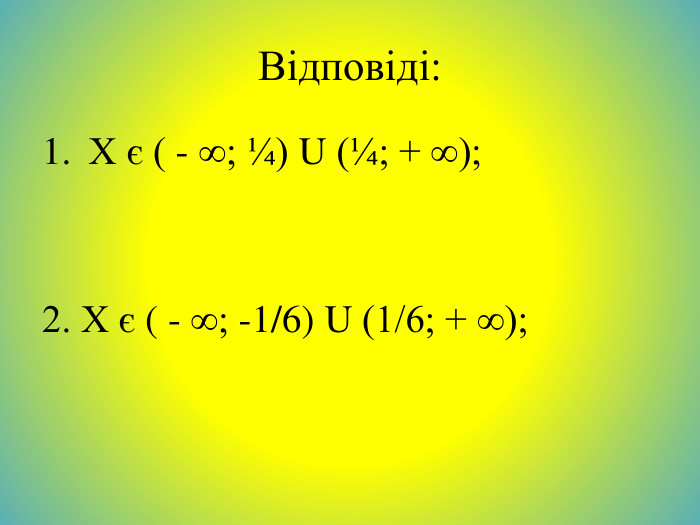
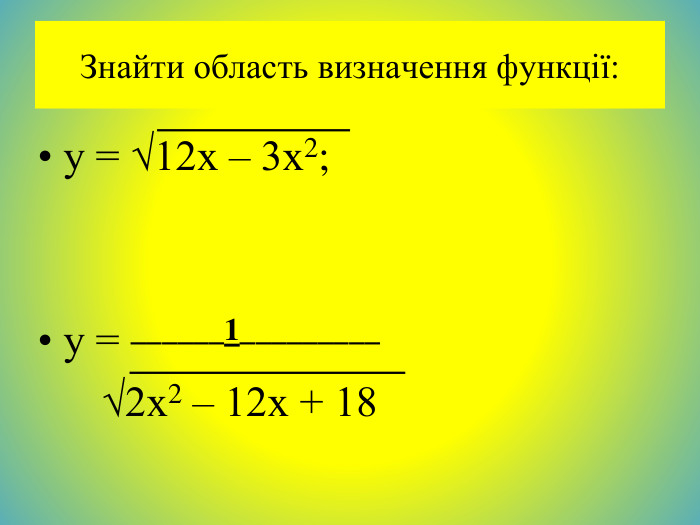
![Відповіді: D(у) = [ 0; 4]2. D(у) = ( - ∞; 3) U (3; + ∞); Відповіді: D(у) = [ 0; 4]2. D(у) = ( - ∞; 3) U (3; + ∞);](/uploads/files/36948/443679/504667_images/84.jpg)
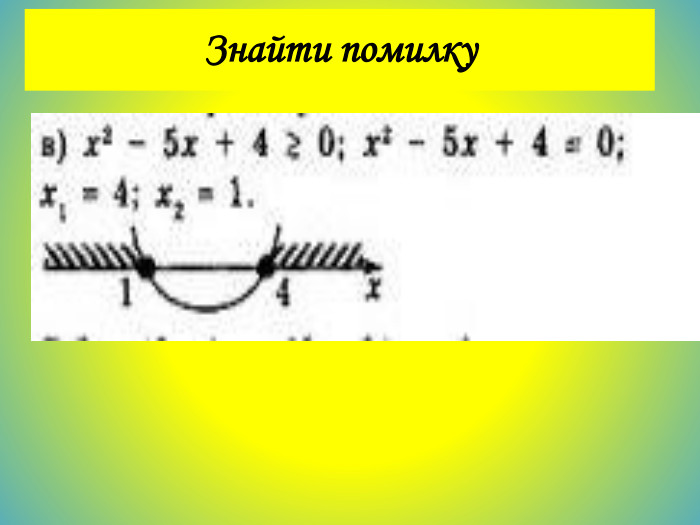

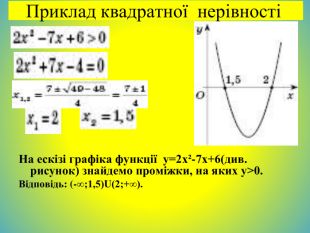
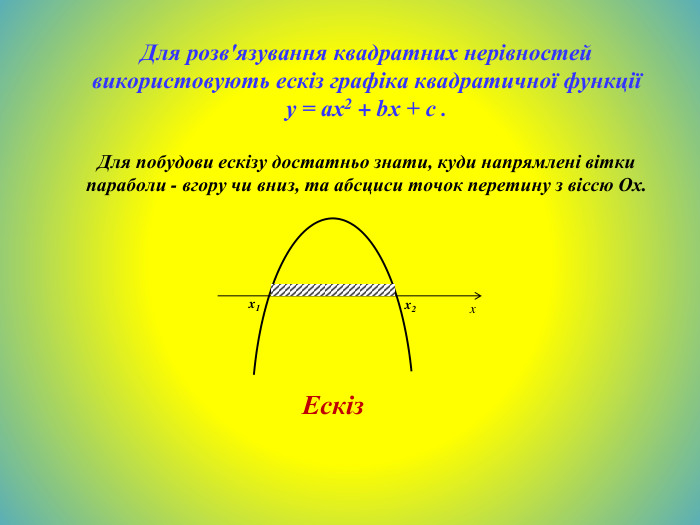
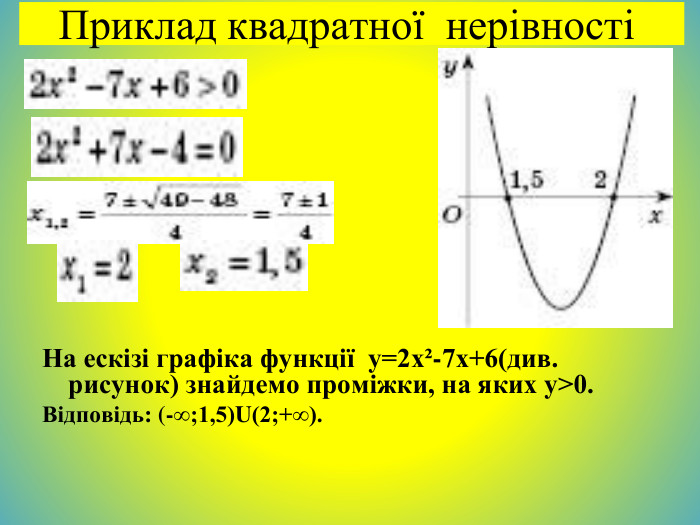
Що таке квадратна нерівність?Якщо лівою частиною нерівності є вираз виду ах²+bx+c , де а не дорівнює 0 , b, c — дані числа, а правою — нуль, то таку нерівність називають квадратною нерівністю. Квадратні нерівності зручно розв’язувати за допомогою графіків квадратичних функцій. Для цього треба:1) знайти корені тричлена ах²+bx+c або з’ясувати, що їх немає;2) зобразити схематично графік функції у=ах²+bx+c , звертаючи увагу тільки на точки перетину з віссю Ox і напрям віток параболи залежно від знака коефіцієнта а;3) знайти на осі Ox проміжки, для яких виконується дана нерівність.
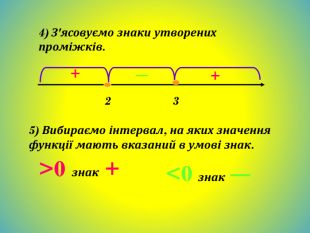
Алгоритм розв'язування квадратних нерівностей (графічний спосіб).1. Визначити напрямок віток параболи в залежності від знака коефіцієнта а.2. Знайти дискримінант D , а потім корені квадратного тричлена (якщо вони існують).3. Побудувати ескіз графіка квадратичної функції у = ах2 + bх + с (з урахуванням знака коефіцієнта а та знайденого знака дискримінанта D і коренів). !!! Для випадку > 0 відповідно отримаємо проміжок, для якого точки параболи лежать вище осі Ох, для випадку < 0 відповідно отримаємо проміжки, для яких точки параболи лежать нижче осі Ох.4. Записати відповідь.
Що таке квадратний тричлен?Квадратним тричленом називається многочлен виду ах²+bx+c , де x — змінна, a, b і c — деякі числа, причому а не дорівнює 0 . Коренем квадратного тричлена називається таке значення змінної, яке перетворює квадратний тричлен на 0. Щоб знайти корені квадратного тричлена, треба розв’язати квадратне рівняння ах²+bx+c=0. Теорема. Якщо х1 і х2- корені квадратного тричлена ах²+bx+c, то ах²+bx+c=а(х-х1)(х-х2) Приклад: 2х2+7х-4=0; а=2;b=7; с=-4; D=b2-4ac=49-4•2•-4=49+32=81=9; х1=0,5; х2=-4;
Рівняння, що зводяться до квадратних. Рівняння виду ах4+bx2+с=0,де а не дорівнює 0, називається біквадратним. Для його розв’язання вводять нову змінну: х2=у, у≥0. Приклад: 4х4-25х2+144=0;Нехай х2=у, у≥0; у2-25у+144=0;Розв’язавши це квадратне рівняння, знайдемо: у1=9; у=16; у=9; у=16; х2=9; х2=16; х1=3, х2=-3, х3=4, х4=-4;Відповідь: х1=3, х2=-3, х3=4, х4=-4;
Розв’язування систем рівнянь. Розглянемо системи рівнянь, в яких одне або обидва рівняння другого степеня. Щоб розв’язати систему рівнянь графічним способом, треба побудувати в одній системі координат графіки обох рівнянь системи й знайти координати точок перетину графіків. Ці точки і будуть розв’язками системи рівнянь. Наприклад: Графіком першого рівняння є коло з центром в точці О(0;0) і радіусом 5 одиничних відрізків. Графік другого рівняння — парабола, вітки якої напрямлені вниз. Точки перетину з осями координат: (0; 5); Система має чотири розв’язки: Перевірка показує, що третій і четвертий розв’язки точні, а не наближені.
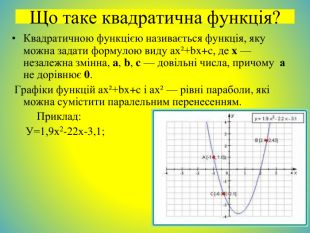
Що таке квадратична функція?Квадратичною функцією називається функція, яку можна задати формулою виду ах²+bx+c, де x — незалежна змінна, a, b, c — довільні числа, причому а не дорівнює 0. Графіки функцій ах²+bx+c і ах² — рівні параболи, які можна сумістити паралельним перенесенням. Приклад: У=1,9х2-22х-3,1;
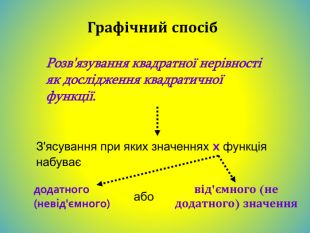
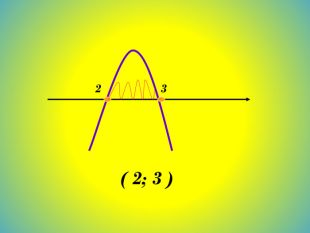
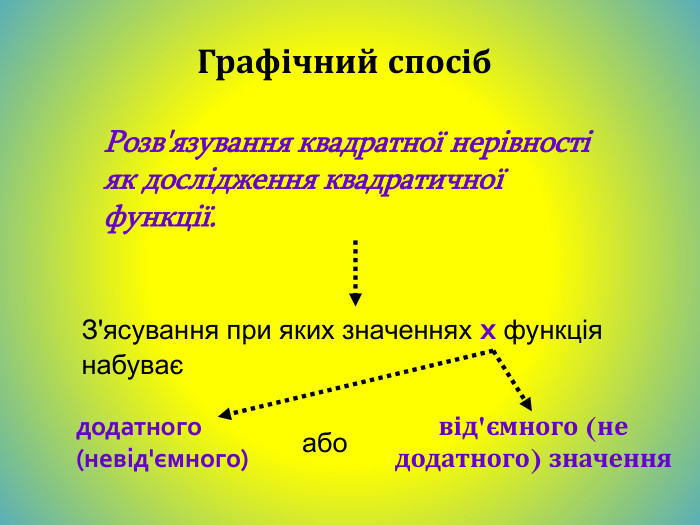
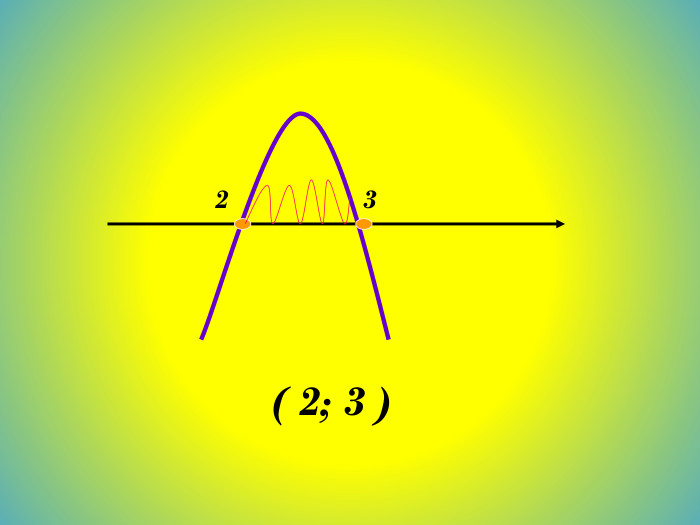
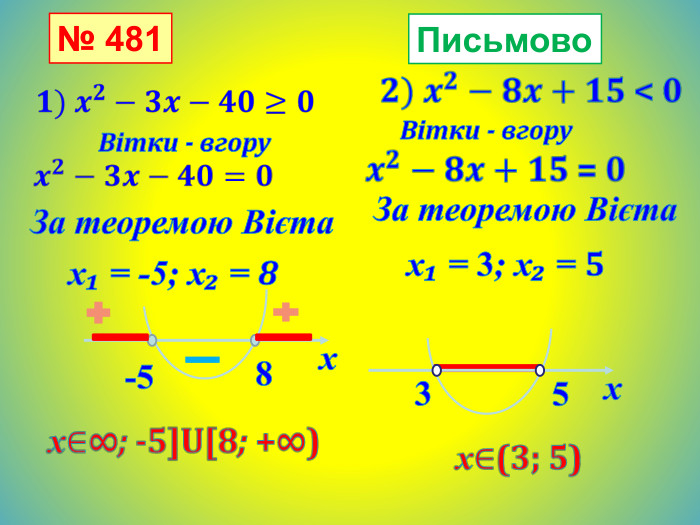
Графічний спосіб. Розв'язування квадратної нерівності як дослідження квадратичної функції. Наприклад:- х² + 5х – 6 > 0 Будуємо зображення параболи відносно осі ОХ.( для цього) а) знаходимо нулі функції;x´=2, x´´=3б) визначаємо розміщення віток параболиа<0, вітки направлені вниз23 Відповідь:( 2; 3 )в) Записуємо відповідь за знаком < або > даної нерівностіЯкщо у>0, то знаходимо відповідний х є (2;3)
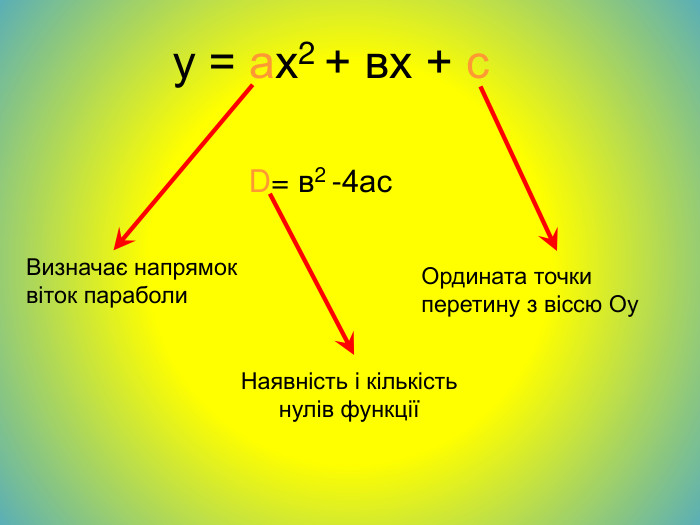
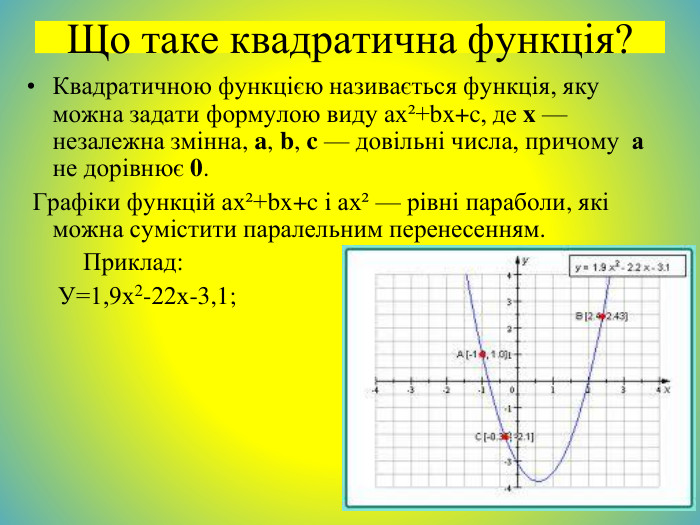
Схема побудови квадратичної функціїПри побудові параболи користуються такими загальними формулами та властивостями квадратичної функції.1. Напрям віток параболи залежить від знака коефіцієнта a .а<0, вітки параболи напрямлені вниз.а>0 вітки параболи напрямлені вгору.2. Точки перетину параболи з осями координат є такими: Абсциса точки перетину параболи з віссю Oy дорівнює 0, тоді ,у(0)=с,(0;с) . Ордината точок перетину параболи з віссю Ox дорівнює 0, тоді, щоб знайти абсциси цих точок, треба розв’язати квадратне рівняння ах²+bx+c=0.3. Координати вершини параболи у=ах²+bx+c; Аналізуємо:1.)D(y); хєR(-∞;+∞) 2.)Е(у); ує [0;+∞) а>0 ує(-∞;0] а<0 3.)х=0; у=0 (0;0)-пер.3ох 3оу4.) Точки перетину графіка з осями координат. 5.)Зростання ;спадання6.)Найбільше,найменше значення функції min;max.
Приклад квадратичної функціїПобудувати графік функції у=х2-4х+3;1.)х>0 вітки параболи напрямлені вгору.2.)Вершини (-2;-1)3.)(1;0),(3;0)Аналізуємо: у1.)D(y) хєR(-∞;+∞)2.)Е(х) ує(-1;-∞) 2 3.)у=0 при х=1 і х=3;х=0 при у=3; -1 х 4.)5.)(-∞;2)-зростає. (2;+∞)-спадає6.)х max= 2 y max=-1{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}х-1012345у830-1038
Розглянемо розв‘язок квадратної нерівності −𝒙𝟐+𝟒𝒙−𝟓>𝟎. y = −𝒙𝟐+𝟒𝒙−𝟓1)Вітки параболи напрямлені вниз, оскільки 𝒂=−𝟏<𝟎.2) 𝒚=𝟎, −𝒙𝟐+𝟒𝒙−𝟓=𝟎 + 𝑫=𝒃𝟐−𝟒𝒂𝒄=𝟏𝟔−𝟐𝟎=−𝟒 𝑫<0, рівняння коренів не має . Графік функції не перетинає вісь Ох. Для будь-якого x з області визначення у<0. Відповідь: x x
1)X²+x-30 < 0Δ=121 , √Δ=11 X1=(-1-11)/2=-6 , x2=(-1+11)/2=5---------o--------o------- > Xxxxxxx -6 5 X ∈ (-6;5)2) 2x²-50x>0 // :2 X²-25>0 X(x-5)>0 X1=0 , x2=5 Xxxxxxx xxxxxx---------o--------o------- > 0 5 X ∈ (-∞;0) U (5;+∞)3)x²+10x+25 ≥0(x+5)² ≥0 X1,2=5------------*---------- > 5 X ∈ R4)3x²-x+2 ≤0Δ=1-24 < 0 коренів немаєX ∈ ∅5)(x+2)² < 13-(x-3)²X²+4x+4 < 13-x²+6x-92x²+10x< 0 // :2 X²+5x < 0 X(x-5)<0 X1=0 , x2=-5 -----o --------o ---- -5 xxxxx 0 X∈ (-5;0)
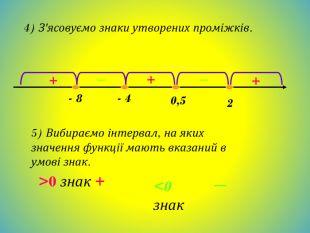
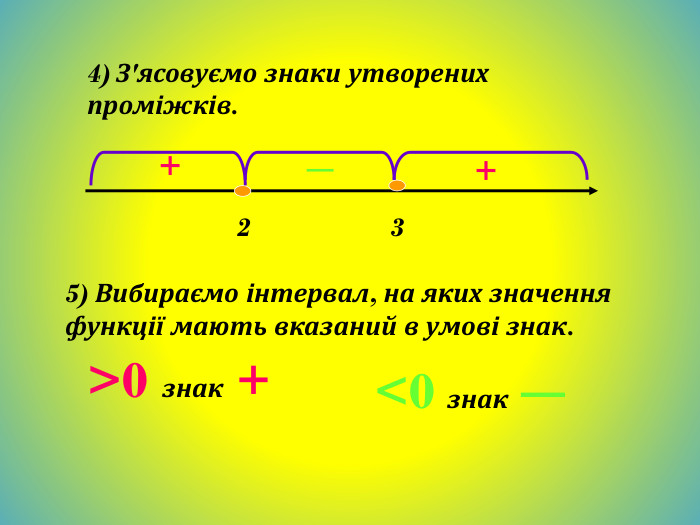
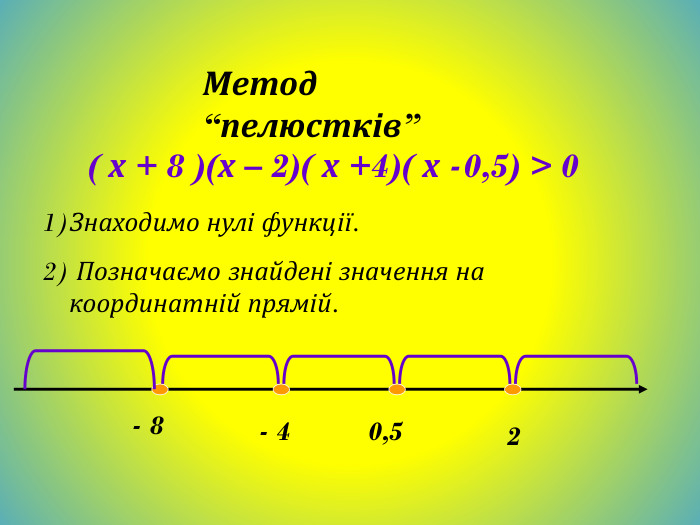
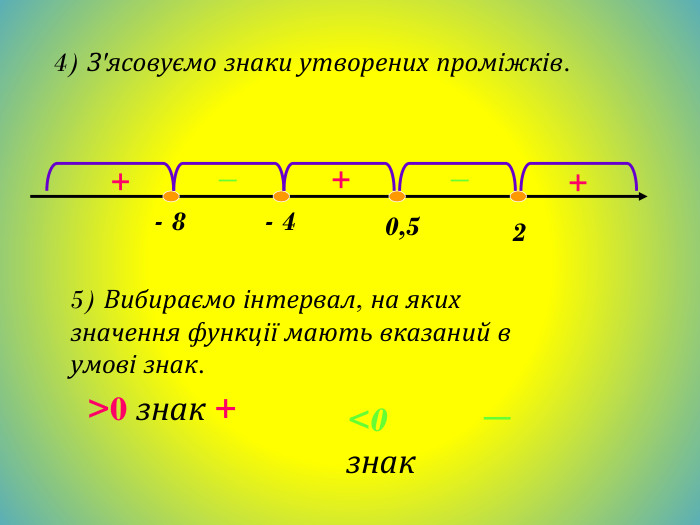
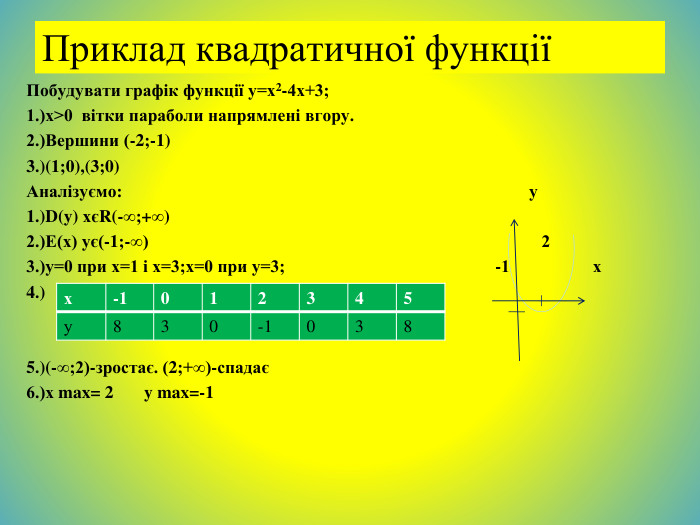
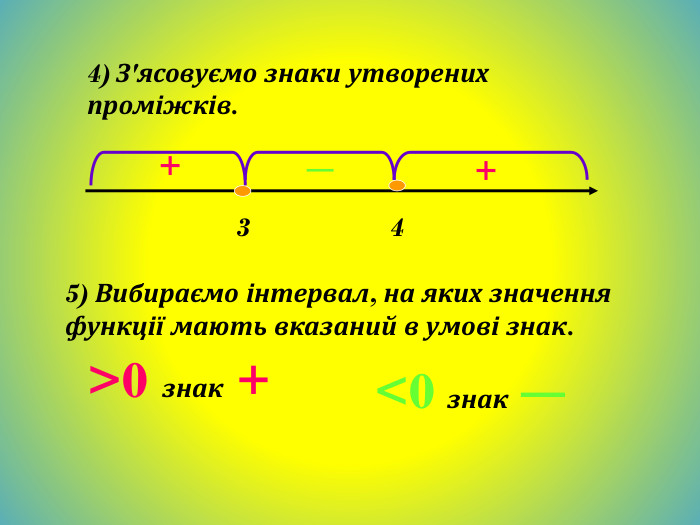
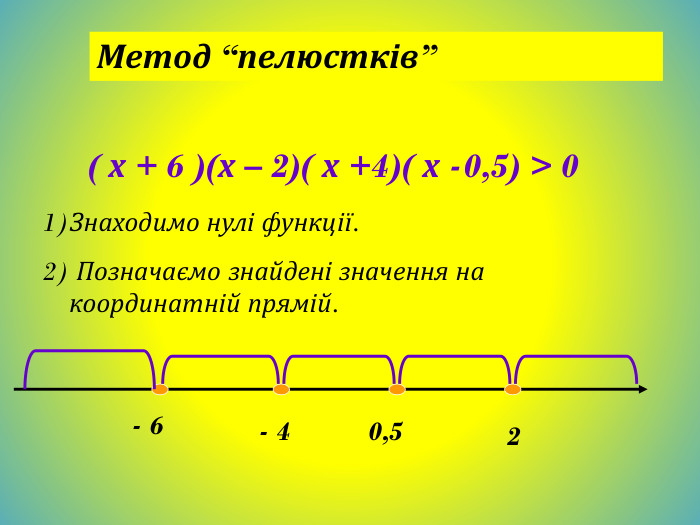
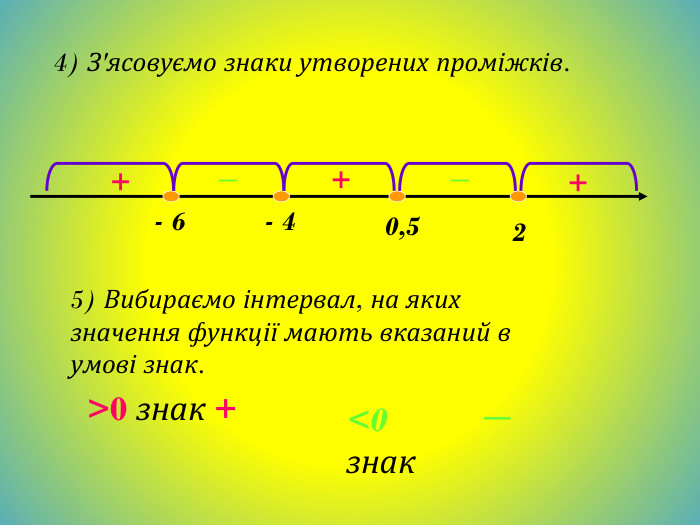
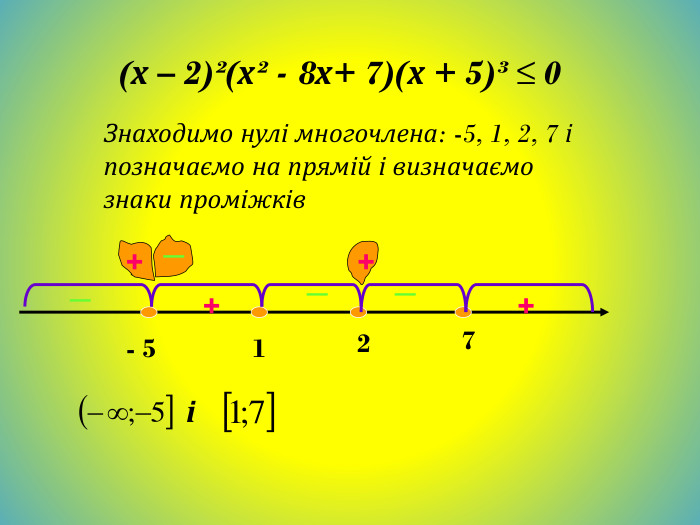
Метод інтервалів. Розв`яжемо нерівність (х+3)(х+2)(х-6)<0;Знайдемо нулі функції. (х+3)(х+2)(х-6)=0;Х+3=0; х+2=0; х-6=0;Х=-3; х=-2; х=6; - + - + -3 -2 6 Відмітимо знаки функції на утворених проміжках (на крайньому праворуч знак +, на решті проміжків - такі знаки, щоб, рухаючись справа на ліво, ці знаки чергувались). Множиною розв`язків нерівності є об`єднання проміжків (-∞;-3) і (-2;6)Відповідь: (-∞;-3)U(-2;6)


про публікацію авторської розробки
Додати розробку