Квадратні рівняння та їх застосування

ТЕМА УРОКУ.  Квадратне рівняння та його використання.

МЕТА УРОКУ: відтворити знання про квадратне рівняння, його види, способи розв'язування; вміння розв'язувати квадратні рівняння. систематизувати та узагальнити навчальні досягнення учнів щодо розв'язання квадратних рівнянь та їх використання в ході уроку та їх використання в ході уроку під час формування компетенцій учнів з алгебри; розвивати увагу, мислення, пам'ять, культуру математичного мовлення; вміння працювати самостійно, вміння спілкуватись, допомагати іншим, аналізувати ситуацію, оцінювати свої дії та дії інших учнів; виховувати уважність, кмітливість, акуратність, працьовитість, самостійність, дисциплінованість, самокритичність.

ТИП УРОКУ: узагальнення та систематизація знань, умінь і навичок.

ІННОВАЦІЙНІ ТЕХНОЛОГІЇ: інтерактивні технології  (робота в групах, «асоціативний кущ»), інформаційно-комунікаційні технології (мультимедійна презентація до уроку), технологія тестування.

ОБЛАДНАННЯ: портрети видатних математиків; мультимедійна презентація [Додаток А.3.],  картки з тестовими завданнями.

План уроку.

1. Організаційний момент.
2.  Актуалізація опорних знань.
3. Систематизація та узагальнення матеріалу.
4. Підведення підсумків уроку.
5. Домашне завдання.

Хід уроку.

І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ

Повідомлення теми, мети та девізу уроку.

Вступне слово учителя.

Квадратні рівняння – це фундаментальне поняття алгебри. Квадратне рівняння знаходить широке використання при розв’язуванні тригонометричних, логарифмичних показникових  рівнянь та нерівностей (з ними ви познайомитесь у старших класах).

Ми живемо у вік науково-технічного прогресу. Однією з його характерних особливостей є те, що в усіх галузях практичної діяльності людини, навіть у таких „традиційно не математичних”, як медицина, лінгвістика, теорія управління виробництвом тощо, застосовується математика, зокрема її розділ – рівняння. Рівняння є надзвичайно результативними моделями багатьох природних, економічних, технічних процесів. Досліджуючи рівняння, можна всебічно вивчити реальний процес, який воно описує, і на підставі здобутих результатів прогнозувати нові характеристики того чи іншого явища. Тож рівняння відіграють дуже велику роль у житті людини.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ.

 

1.   Дайте означення квадратного рівняння? ( )
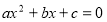2.   За даним означенням, знайдіть квадратні рівняння серед запропонованих? (1, 3, 4, 6)
3.   Дайте класифікацію видів квадратних рівнянь?
4.   Які способи розв’язання повних квадратних рівнянь вам відомі?
5.   Сформулюйте теорему Вієта?
6.   Щоб знайти корені квадратного рівняння треба знайти дискримінант. Хто нагадає нам його формулу та обмеження, що накладаються?
7.   Охарактеризуйте перший вид неповних квадратних рівнянь?
8.   Охарактеризуйте другий вид неповних квадратних рівнянь?
9.   Охарактеризуйте третій вид неповних квадратних рівнянь?

 

ІІІ. СИСТЕМАТИЗАЦІЯ ТА УЗАГАЛЬНЕННЯ  ЗНАНЬ.

Працюємо усно!!!

І. Знайдіть зайве рівняння, завдання для кожної з груп. Поясніть свій вибір та обґрунтуйте відповідь.

А – зайве 3.        Б – зайве 2.       В – зайве 3.

ІІ. Не розв’язуючи рівнянь знайдіть їх корені. Кожна з груп по черзі коментує рівняння.

а) х=6, х=-13                  в) х=0, х=4                             д) х=0

б) х=0, х=-0,7                 г) х=1/4, х=-1/4                     ж) х=-3, х=11.

ІІІ. Яке з рівнянь не має коренів? Відповідає команда, за бажанням.

, тому що .

ІV. Перевір себе! Кожна група виписує рівняння кожного типу.

      1 – повні;    2 – неповні;    3 – зведені.

Далі продовжуємо роботу у групах.

1.         Кожна група має своє завдання. За 2-3 хвилини треба обговорити і записати схематично на аркуші ватману алгоритм розв’язування квадратних рівнянь і розв’язати приклад (2 доповідача).

І група. – повні квадратні рівняння.

ІІ група. – неповні квадратні рівняння, якщо a0, b=0, c0

ІІІ група. - неповні квадратні рівняння, якщо a0, b0, c=0

2.         Рівняння називають мовою алгебри. Тому кожен із математиків повинен знати не один, а кілька способів розв’язування рівнянь.

 Пропонується розв’язати кв. рівняння різними способами:

 І група  - виділивши в його лівій частині квадрат двочлена

ІІ група – за допомогою формули коренів квадратного рівняння

IІІ група – графічним способом

3.         Але недостатньо вміти тільки розв’язувати рівняння, а необхідно творчо застосовувати свої зання, вміти досліджувати рівняння.

     Зараз пропоную переглянути приклади та знайти помилки, яких я допустилася при їх розв’язуванні.

4.   Ми узагальнили знання про квадратні рівняння, і ще раз переконалися що математика не розвивається сама, всі відкриття в ній роблять люди. Так, свій внесок у розвиток учення про рівняння зробили вчені: Мухаммед аль-Хорезмі, Евклід, Франсуа Вієт, Омар Хайям.

 Розв’язавши рівняння, які написані на картках, ви отримаєте відповіді. Знайдіть ці відповіді на оборотній стороні інших карток. Складіть картки з текстами одна до одної та отримайте невеличкі розповіді про цих вчених. Давайте їх прослухаємо:

                            І група – Евклід

ІІ група – Франсуа Вієт

ІІІ група – Омар Хайям

Ці вчені , про яких ми сьогодні говорили не обмежувалися лише математикою, вони були високо освіченими і всебічно розвинутими в різних галузях наук. До цього ж повинні прагнути і ви.

А зараз пропоную пройти тест, який покаже результати вашої роботи.

 тест «Квадратні рівняння»          

За результатами  якого вам буде додано відповідну кількість балів.    

1 варіант	2 варіант
Закриті завдання
Яке з рівнянь є квадратним?  А. 3 – 5х + 2 =0 В. 9х + 3х² – 10 = 0 С. 0х² – 15 х + 1 = 0 D. 5х² + 2,7/х + 1 = 0	Яке з рівнянь є квадратним? А. 0х²+5х-3=0 В. 3х+х²-10=0 С. 2х²+7/х+3=0 D. 4х³-2х+5=0
Складіть квадратне рівняння з його коефіцієнтами a, в,c: а=-2; b= 3,5; c=0,75. -2х²-0,75х+3,5=0 3,5х²-2х+0,75=0 - 2х²+3,5х+0,75=0 - 2х²+3,5х-0,75=0	Складіть квадратне рівняння з його коефіцієнтами a, в,c: а=-8; b= 0,5; c=5,3. А. - 8х²+5,3+0,5=0 В. - 8х²-0,5х+5,3=0 С. 0,5х²+8х+5,3=0 D. - 8х²+0,5х+5,3=0
Вкажіть коефіцієнти квадратного рівняння:                 -5х²+3х-2=0.  А. а=-5, в=3, с=2 В. а=-5, в=3, с=-2 С. а=-5, в=-3, с=-2	Вкажіть коефіцієнти квадратного рівняння:                   -3х²-5х+2=0.  А. а=-3, в=5, с=2 В. а=-3, в=5, с=-2 С. а=-3, в=--5, с=2
Зведіть рівняння до стандартного вигляду:           -4х-3х²+5х=7  А. 2х²+4х+7=0 В. - 8х²-4х-7=0 С. 2х²-4х-7=0	Зведіть рівняння до стандартного вигляду:            2х²+3х-7х=8  А. -5х²+3х+8=0 В. -9х²+3х-8=0 С. -5х²+3х-8=0
Виберіть серед наведених рівнянь неповні квадратні: 1) 3х³=0; 2) х²+4х=192; 3) 7х²-3=0; 4)5у²=10у; 5)х²=6. А. 1,2,3 В. 2,3 С. 3,4,5 D. 2,3,4,5	Виберіть серед наведених рівнянь неповні квадратні: 1) 1-4у²=0; 2) 7а-14=0; 3) 4х-12=3х²; 4)х²=5; 5)7а²=14а. А. 1,2,3 В. 1,4,5 С. 1,3,4,5 D. 4,5
Скільки коренів має рівняння:      - 5х²+3х=0 ? А. два В. один С. нет корней	6. Скільки коренів має рівняння:      3х²-7х=0 ? А. два В. один С. нет корней

 

ІV. ПІДВЕДЕННЯ ПІДСУМКІВ УРОКУ.

Оцінки за роботу на уроці будуть скомпоновані з оцінками за тест, та виставлені та повідомлені на початку наступного уроку.

А зараз прийшов час підвести підсумки сьогоднішнього уроку. Пропоную зробити це у наступним чином.

Вправа: «Продовж речення»

1. Сьогодні на уроці ми….
2. Мені сподобалось….
3. Я навчився (лася)…..

 

V.                 ДОМАШНЕ ЗАВДАННЯ. Опрацювати §

 

 

Виставлення і аргументація оцінок

 

 

 

Додаток 1

Картки для роботи в групах

 

 

І група

Завдання № 1

Записати на аркуші ватману схему розв’язування повного квадратного рівняння.

Розв’язати приклад:

Завдання № 2

Розв’язати квадратне рівняння виділивши в його лівій частині квадрат двочлена

 

 

 

ІІ група

Завдання № 1

Записати на аркуші ватману схему розв’язування неповного квадратного рівняння, якщо a0, b=0, c0

Розв’язати приклад:

Завдання № 2

Розв’язати квадратне рівняння за допомогою формули коренів квадратного рівняння

 

 

 

ІІІ група

Завдання № 1

Записати на аркуші ватману схему розв’язування неповного квадратного рівняння, якщо a0, b0, c=0

Завдання № 2

Розв’язати квадратне рівняння розклавши на множники ліву частину способом групування

Додаток 2

І група

Картка-завдання

 

 

 

 

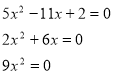
Картка-відповідь

Евклід – один з найвидатніших давньогрецьких математиків. Жодних біографічних відомостей про його життя не збереглося. Відомо тільки, що на запрошення царя Птолемея Евклід приїхав у ІІІ ст. до н.е. в м. Александрію – резиденцію грецьких царів у Єгипті – і почав там працювати наглядачем

славнозвісної бібліотеки. У бібіліотеці зберігалися й математичні праці вчених – попередників Евкліда. Проте вони були розрізненими і несистематизованими. Учений довгі роки працював над упорядкуванням математичної спадщини попередніх поколінь і створив велику працю, що складалася з 13 книг і дістала назву “Начала”.

Спочатку Евклід сформулював п’ять аксіом про ознаки рівності і нерівності величин і п’ять постулатів, тобто вимог, додержання яких дає можливість виконувати всі геометричні побудови. На підставі цих первинних незаперечних суджень, що приймаються без доведення, учений будує систему теорем, які вже доводить дедуктивно.

 

 

ІІ група

Картка-завдання

 

 

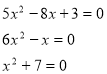
Картка-відповідь

Французький вчений (1540-1603), зробив вагомий внесок для розвитку математики, вважається “батьком сучасної алгебри”: написав першу у світі роботу з символічної алгебри. Вієт увів буквені позначення невідомих, саме від нього бере початок сучасна алгебраїчна символіка. Захопившись якоюсь математичною задачею, він міг працювати над нею іноді три доби без їжі і сну.

В останні роки свого життя Вієт був радником французьких королів Генріха ІІІ і Генріха IV. Під час війни між Фанцією та Іспанією іспанці застосували для таємного листування дуже складний шифр. Завдяки цьому Іспанія мала можливість вільно підтримувати зв’язки  з супротивниками французького короля навіть у межах Франції. Після безрезультатних пошуків ключа до цього шифру король Генріх Четвертий звернувся за допомогою до Франсуа Вієта. Вчений відразу відгукнувся на це прохання. Він працю-

вав вдень і вночі упродовж двох тижнів, доки задачу не було розв’язано. Вчений не тільки розгадав цей складний шифр, але й указав спосіб, як слідкувати за всіма його змінами. Після цього Генріх Четвертий зробив Вієта своїм особистим радником.

Іспанці довгий час не могли зрозуміти причини своїх невдач у військових справах. Нарешті з таємних джерел стало відомо, що їхній шифр для французів уже не є секретом і винний у його розшифруванні Франсуа Вієт. За це іспанська інквізиція заочно засудила вченого до страти. Коренів немає.

 

 

IІІ група

Картка-завдання

 

 

 

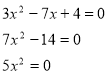
Картка-відповідь

Народився Омар Хайяма у 1048 р. В місті Нішапурі, що на півдні від Ашхабада. Жив і працював у Самарканді, Бухарі, Ісфагані, інших містах Середньої Азії та Ірану. Повне ім’я цієї людини складається з багатьох слів: Хайям Омар Гіяседдін Абу-аль Фахт.

У молодості він захоплювався астрономією і математикою, пізніше географією, філософією, поезією. Перший його твір до нас не дійшов.

Та ми знайомі з його працею-трактатом “Про доведення задач алгебри і ал-мукабали”. Тут подано класифікацію рівнянь 1-го, 2-го і 3-го порядків, стверджується, що алгебра – наука про знаходження невідомих за допомогою рівнянь (че перше означення алгебри як науки, що дійшло до нас).

У сучасному світі Омар Хайям відомий як поет, автор філософсько-ліричних чотирирядкових віршів, об’єднаних у збірку “Рубайат” (рубаї – один з найважчих жанрів таджицько-перської літератури.)