Теорема Вієта та її застосування
ТЕМА УРОКУ. Теорема Вієта.
МЕТА УРОКУ: формувати навички та вміння застосовувати теорему Вієта і теорему, обернену до неї, до розв’язування квадратних рівнянь; вміти узагальнювати, проводити міркування за аналогією; розвивати комунікативні навички учні; виховувати бажання працювати; розвивати пізнавальні інтереси.
ТИП УРОКУ: комбінований урок.
ІННОВАЦІЙНІ ТЕХНОЛОГІЇ: інтерактивні технології (індивідуальна робота, «асоціативний кущ»), інформаційно-комунікаційні технології (мультимедійна презентація до уроку), технологія розвитку критичного мислення (математичний диктант, самостійна робота).
ОБЛАДНАННЯ: картки із завданнями, опорні схеми [Додаток А.4.], мультимедійна презентація [Додаток А.5.]
ДЕВІЗ: Розумова праця на уроках математики – пробний камінь мислення.
В.А. Сухомлинський
ЕПІГРАФ: Рівняння – це золотий ключ,
який відкриває всі математичні таємниці.
С. Коваль
ХІД УРОКУ
І. Організаційний момент.
ІІ. Перевірка домашнього завдання.
- Наявність письмового домашнього завдання перевіряють чергові або консультанти.
- Індивідуальна робота.
Чотири учні розв’язують рівняння записані на картках за партами.
Розв’язати рівняння.
а) х2 – 8х + 15 = 0;
б) х2 – 2х – 35 = 0;
в) х2 – 7х +12 = 0;
г) х2 – 10х + 24 = 0.
Розв’язання.
а) D = 64 – 60 = 4 > 0, тому корені існують.
За теоремою Вієта: ![]()
звідки х1 = 3, х2 = 5. Відповідь: 3;5.
б) D = 4 + 140 = 144 > 0, тому корені існують.
За теоремою Вієта: ![]()
звідки х1 = -5, х2 = 7. Відповідь: -5;7.
в) D = 49 – 48 = 1 > 0, тому корені існують.
За теоремою Вієта: ![]()
звідки х1 = 3, х2 = 4. Відповідь: 3;4.
г) D = 100 – 96 = 4 > 0, тому корені існують.
За теоремою Вієта: ![]()
звідки х1 = 4, х2 = 6. Відповідь: -5;7.
- Розв’язати квадратне рівняння.
Чотири учні розв’язують рівняння записані на картках біля дошки.
Розв’язати рівняння.
а) 5х2 – 8х + 3 = 0; б) х2 + 2х – 3 = 0;
в) 5х2 + 8х +3 = 0; г) х2 – 2х - 3 = 0.
Розв’язання.
а) D = (-8)2 – 4·5·3 = 64 – 60 = 4 = 22 > 0;
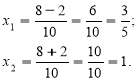
Відповідь: ![]()
б) D = 4 + 12 = 16 > 0, тому корені існують.
За теоремою Вієта: ![]()
звідки х1 = -3, х2 = 1.
Відповідь: -3;1.
в) D = 82 – 4·5·3 = 64 – 60 = 4 = 22 > 0;
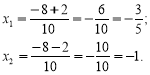
Відповідь: ![]()
г) D = 4 + 12 = 16 > 0, тому корені існують.
За теоремою Вієта: ![]()
звідки х1 = -1, х2 = 3.
Відповідь: -1;3.
- Математичний диктант.
(Один учень працює біля дошки на зворотній стороні, а інші самостійно в зошитах. Здійснюється взаємоперевірка)
-
(1 бал) Рівняння, що має вигляд,
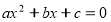 де х – змінна, а, b, с – довільні числа, при чому а ≠ 0, називають … (квадратним)
де х – змінна, а, b, с – довільні числа, при чому а ≠ 0, називають … (квадратним)
- (1 бал) Вираз b2 – 4aс називають … квадратного рівняння. (дискримінантом)
- (1 бал) Якщо в квадратному рівнянні перший коефіцієнт дорівнює одиниці, то його називають … (зведеним)
- (1 бал) Квадратне рівняння називають ще рівнянням другого … (степеня)
- (1 бал) Якщо дискримінант квадратного рівняння дорівнює нулю, то рівняння має один … (корінь)
- (1 бал) Якщо хоча б один з коефіцієнтів b або с квадратного рівняння дорівнює нулю, то рівняння називають … (неповним)
- (1 бал) Для обчислення коренів квадратного рівняння існує … (формула)
- (1 бал) Якщо дискримінант є від’ємним числом, то рівняння не має … розв’язків (дійсних)
- (1 бал) Число a в квадратному рівнянні називають першим … (коефіцієнтом)
- (1 бал) Квадратне рівняння має два різні корені, якщо дискримінант є … числом (додатним)
- (1 бал) Якщо значення виразу b2 – 4aс = 0, то рівняння має … розв’язки
(два однакові дійсні)
- (1 бал) Зведені квадратні рівняння розв’язуються за теоремою, оберненою до теореми … (Вієта)
- Колективне розв’язування рівнянь за властивостями коефіцієнтів квадратного рівняння.
Якщо а + в + с = 0, то х1 = 1, ![]() якщо а – в + с = 0, то х1 = -1,
якщо а – в + с = 0, то х1 = -1, ![]()
Розв’язати рівняння.
а) 17х2 – 15х - 2 = 0;
б) 71 х2 + 75х + 4 = 0.
Розв’язання.
а) а + в + с = 17 – 15 – 2 = 0.
Тому х1 = 1, ![]()
Відповідь: 1; ![]()
б) а – в + с = 71 – 75 + 4 = 0.
Тому х1 = -1, ![]()
Відповідь: -1; ![]()
ІІІ. Мотивація навчання.
Теорема, обернена до теореми Вієта, дає можливість перевірити, чи є та чи інша пара чисел коренями квадратного рівняння. Користуючись оберненою теоремою, можна також складати зведене квадратне рівняння, якщо відомі його корені.
ІV. Сприймання й усвідомлення теореми, оберненої до теореми Вієта.
Для того, щоб утворити твердження, обернене до даного, в ньому треба поміняти місцями умову та висновок. Щоб легше з’ясувати, що є умовою, а що висновком, твердження доцільно формулювати у вигляді «Якщо …, то…». Тоді те, що записано перед «то», є умовою, після «то» висновком.
Теорема, обернена до теореми Вієта, читається так:
Якщо дійсні числа х1 та х2 такі, що ![]() то ці числа х1 та х2 є коренями зведеного квадратного рівняння. (Пропонуємо сильнішим учням довести теорему вдома.)
то ці числа х1 та х2 є коренями зведеного квадратного рівняння. (Пропонуємо сильнішим учням довести теорему вдома.)
V. Осмислення вивченого матеріалу.
-
Скласти зведене квадратне рівняння, коренями якого є числа (колективно):
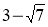 і
і 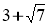 .
.
Розв’язання.
Шукане рівняння має вигляд: ![]() де
де
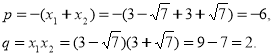
Отже, шукане рівняння: ![]()
Відповідь: ![]()
- Самостійна робота.
- (1 бал) Скласти зведене квадратне рівняння, коренями якого є числа: -2 і 7.
-
(1 бал) У рівнянні
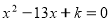 один із коренів дорівнює 5. Знайти k та другий корінь рівняння.
один із коренів дорівнює 5. Знайти k та другий корінь рівняння.
-
(2 бали) Корені х1 та х2 рівняння
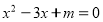 задовольняє умову
задовольняє умову 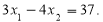 Знайти значення m та корені рівняння.
Знайти значення m та корені рівняння.
-
(2 бали) Не розв’язуючи рівняння знайти:
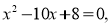 знайти
знайти 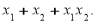
-
(2 бали) Знайти значення виразу:
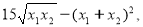 де х1 та х2 – корені рівняння:
де х1 та х2 – корені рівняння: 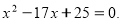
-
(2 бали) Корені х1 та х2 рівняння
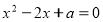 задовольняє умову
задовольняє умову 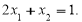 Знайти значення а.
Знайти значення а.
-
(2 бали) х1 та х2 - корені рівняння
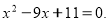 Не розв’язуючи рівняння, знайти:
Не розв’язуючи рівняння, знайти: 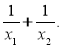
Розв’язання.
-
Шукане рівняння має вигляд:
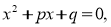 де
де
![]()
Отже, шукане рівняння: ![]()
Відповідь: ![]()
-
За теоремою Вієта:
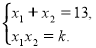
За умовою х1 = 5.
Тоді маємо: ![]()
![]()
Отже, k = 40.
Відповідь: 40.
-
За теоремою Вієта:

Враховуючи умову: ![]() складемо та розв’яжемо систему рівнянь:
складемо та розв’яжемо систему рівнянь: ![]()
![]()
звідки 7х1 = 49, х1 = 7. Якщо х1 = 7, то 7 + х2 = 3, х2 = 3 – 7 = - 4.
Тоді m = 7·(-4) = -28. Відповідь: 7; -4; -28.
-
За теоремою Вієта:
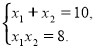
Тому ![]()
Відповідь: 18.
-
За теоремою Вієта:
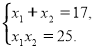
Тоді ![]()
Відповідь: -214.
-
За теоремою Вієта:
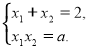
Враховуючи умову: ![]() складемо систему рівнянь:
складемо систему рівнянь:
![]()
![]()
звідки х1 = -1. Якщо х1 = -1, то -1 + х2 = 2, х2 = 2 + 1 = 3,
а = -1·3 = -3. Відповідь: -3.
-
За теоремою Вієта:
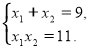
Тоді маємо: ![]() Відповідь:
Відповідь: ![]()
VІ. Підсумок уроку.
На уроці детальніше розглянули знаходження коренів зведеного квадратного рівняння; зробили висновок щодо розв’язування повних рівнянь; ознайомились з теоремою, оберненою до теореми Вієта, яка дає можливість, знаючи корені, скласти зведене квадратне рівняння; приділити увагу розв’язуванню рівнянь з параметрами.
VІІ. Домашнє завдання.
Самостійна робота.
- Скласти зведене квадратне рівняння, коренями якого є числа: -7 і 3.
-
Скласти зведене квадратне рівняння, коренями якого є числа:
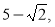
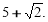
-
Число 8 є коренем рівняння
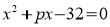 Знайти значення p та другий корінь рівняння.
Знайти значення p та другий корінь рівняння.
-
Не розв’язуючи рівняння знайти:
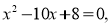 знайти
знайти 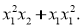
-
х1 та х2 - корені рівняння
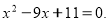 Не розв’язуючи рівняння, знайти:
Не розв’язуючи рівняння, знайти: 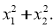
-
х1 та х2 - корені рівняння
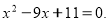 Не розв’язуючи рівняння, знайти:
Не розв’язуючи рівняння, знайти: 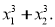
Розв’язання.
-
Шукане рівняння має вигляд:
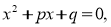 де
де
![]()
Отже, шукане рівняння: ![]()
Відповідь: ![]()
-
Шукане рівняння має вигляд:
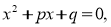 де
де
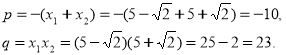
Отже, шукане рівняння: ![]() Відповідь:
Відповідь: ![]()
-
За теоремою Вієта:
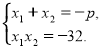
За умовою х1 = 8. Тому маємо: 8х2 = -32, х2 = -4.
Отже, p = -(8 – 4) = -4. Відповідь: -4;-4.
-
За теоремою Вієта:
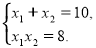
Тому ![]() Відповідь: 80.
Відповідь: 80.
-
За теоремою Вієта:
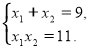
Тоді маємо: ![]() Відповідь: 59.
Відповідь: 59.
-
За теоремою Вієта:
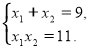
Тоді маємо: ![]()
Відповідь: 432.
Додаток №1
Самостійна робота.
- Скласти зведене квадратне рівняння, коренями якого є числа: -7 і 3.
-
Скласти зведене квадратне рівняння, коренями якого є числа:
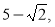
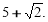
-
Число 8 є коренем рівняння
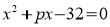 Знайти значення p та другий корінь рівняння.
Знайти значення p та другий корінь рівняння.
-
Не розв’язуючи рівняння знайти:
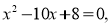 знайти
знайти 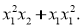
-
х1 та х2 - корені рівняння
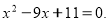 Не розв’язуючи рівняння, знайти:
Не розв’язуючи рівняння, знайти: 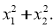
-
х1 та х2 - корені рівняння
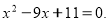 Не розв’язуючи рівняння, знайти:
Не розв’язуючи рівняння, знайти: 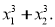


про публікацію авторської розробки
Додати розробку
