Лекція "Інформаційні системи та інформаційні технології"

Модуль1. Логіка і алгебра висловлювань.

Змістовий модуль 1. . Алгебра висловлювань та їх застосування

Тема 1. Алгебра висловлювань

 

Висловлювання і операції над ними

 

План:

1. Висловлення й  форми висловлювання
2. Елементарні й складені пропозиції
3. Операції над висловлюваннями

 

1. Висловлення й  форми висловлювання.

 

Висловлювання - це пропозиція, яка або істинно, або неправильно. Наприклад, висловлення «Москва — столиця СРСР» є дійсним, а висловлення «Волга впадає в Чорне море» — неправильним. Не всяка пропозиція є висловленням.

Так, до висловлень не ставляться питальні й окличні речення, оскільки говорити про їхню істинність або хибність нема рації. Не є висловленнями й такі пропозиції: «Каша — смачне блюдо», «Математика — цікавий предмет»; немає й не може побут& єдиної думки про те, дійсні ці пропозиції або неправильні. Пропозицію «Існують інопланетні цивілізації» слід уважати  висловленням, тому що об'єктивно воно або дійсне, або неправильне, хоча ніхто поки не знає, яке саме. Пропозиції «Ішов сніг», «Площа кімнати рівна 20 м²», а²= =4 не є висловленнями; для того щоб мало сенс говорити про їхню істинність або хибність, потрібні додаткові відомості: коли й де йшов сніг, про яку конкретну кімнату мова йде, яке число позначене буквою а. В останньому прикладі а може не позначати конкретного числа, а бути змінної, тобто буквою, замість якої можна підставляти елементи деякої множини, називані значеннями змінної. Нехай наприклад, {-2; 0; 2, 3, 4} — множина значень змінної а. Кожному значенню змінної відповідає або дійсне, або неправильне висловлення; наприклад, висловлення (-2)²=4, 2²=4 дійсні, а висловлення 0²=4, 3²=4, 4²=4 неправильні.

Пропозиція, яка містить хоча б одну змінну й стає висловленням при підстановці замість усіх змінних їхніх значень, називають формою висловлювання. Розглянемо пропозиції: «Він рудоволосий»; «Число ділиться на 7». Ці пропозиції не містять змінних у явному виді, але проте є формами висловлювання: перше з них стає висловленням (дійсним або неправильним) тільки після заміни займенника «він» іменем конкретної людину з деякого великий кількості людей чоловічої статі; друге стає висловленням, якщо на місце слова «число» підставляти цілі числа. Інакше ці пропозиції можна записати так: «Людей х рудоволосий», «Число в ділиться на 7», З форм висловлювання можна одержувати висловлення не тільки підстановкою замість змінних їхніх значень, але й за допомогою спеціальних слів: «усякий» (а також його синонімів «будь-який», «кожний») і «існує» (а також виражень «деякі», « щонайменше один»). Наприклад, висловлення «Усяке число в ділиться на 7» — неправильне; висловлення «Існує число в, яке ділиться на 7» — дійсне.

 

2. Елементарні й складені пропозиції

 

Із двох даних пропозицій можна утворювати нові предло- жения за допомогою союзів «і», са>, «або», «або», «якщо... те...», «тоді й тільки тоді, коли й ін. За допомогою частки «не» або словосполучення «невірно, що» і з одного пропозиції можна одержати нове. Найбільш уживаними є союзи «і», «або», «якщо... те», «тоді й тільки тоді, коли» (останні два особливо часто вживаються в математику). Кожний з інших союзів або близький за змістом до якого-небудь із зазначених, або може бути замінений їхньою комбінацією із часткою «не». Так, наприклад, союзи «а», «але» близькі за змістом союзу «і». Замість того щоб сказати: «Я піду в театр, або в кіно», можна виразитися більш длинно: «Я піду в театр і не піду в кіно, або піду в кіно й не піду в театр».

Союзи «і», «або», «якщо,., те,..», «тоді й тільки тоді, коли» і частку «не» (словосполучення «невірне, що») будемо називати логічними зв'язуваннями. Пропозиції, утворені з інших пропозицій за допомогою логічних зв'язувань (або союзів, до них, що зводяться), називають складовими. Пропозиції, що не є складовими, будемо називати елементарними.

Так, наприклад, з елементарних пропозицій «Я поїду в Ленінград» і «Ти поїдеш у Київ» можна утворювати наступні складені пропозиції: «Я поїду в Ленінград і ти поїдеш у Київ»; «Я поїду в Ленінград або ти поїдеш у Київ»; «Якщо я поїду в Ленінград, то ти поїдеш у Київ»; «Я поїду в Ленінград тоді й тільки тоді, коли ти поїдеш у Київ»; «Я не поїду в Ленінград»; «Невірно, що ти поїдеш у Київ».

У граматиці розрізняють пропозиції проста й складні. Пропозиція, простої по своїй граматичній структурі, може бути з погляду логіки складовим. Наприклад, проста пропозиція «Протилежні сторони паралелограма конгруэнтны й паралельні» уважається в логіку складовим; воно утворене за допомогою логічного зв'язування «і» з елементарних пропозицій «Протилежні сторони паралелограма конгруэнтны» і «Протилежні сторони паралелограма паралельні». Проста пропозиція «Завтра не буде опадів» по своїй логічній структурі не є елементарним; воно утворене з елементарної пропозиції «Завтра будуть опади» за допомогою логічного зв'язування «не». чи Можна затверджувати, що складена пропозиція є висловленням, якщо всі складові його елементарні пропозиції — висловлення? Розглянемо пропозицію «Число 2 -простої або число 2 --парне». Воно складене із двох дійсних висловлень. Однак розв'язати питання про істинність або хибність цієї пропозиції можна тільки після з'ясування змісту, який має в цьому випадку союз «або».. Якщо мається на увазі розділовий зміст цього союзу ( як, наприклад, у пропозиції «Дві прямі на площині паралельні або перетинаються»), те ми повинні вважати розглянуту пропозицію неправильним; мається на увазі нерозділовий зміст «або» ( як у пропозиції «На пошті можна відправити посилку або підписатися на газету»), та дана пропозиція дійсна. У математичній логіці зміст логічних зв'язувань уточнюється так, щоб питання про істинність або хибність складених пропозицій, утворених з висловлень, у всіх випадках вирішувався однозначно; у результаті цього всяка пропозиція, складене з висловлень за допомогою логічних зв'язувань, стає висловленням.

3. Операції над висловлюваннями

 

3.1 Кон’юнкція

 

Нехай А и В — довільні висловлення. Уведемо символ /\ для позначення союзу «і». Якщо, наприклад, буквою А позначена пропозиція «Завтра буде тепла погода», а буквою В- «Завтра не буде опадів», то вираження А /\В відповідає пропозиції «Завтра буде тепла погода й (завтра) не буде опадів». Якщо завтра виявиться, що погода холодна, або йде дощ, або одночасно йде дощ і холодно, то, усякий, безсумнівно, визнає такий прогноз неправильним; дійсним цей прогноз буде вважатися тільки в тому випадку, якщо виявляться дійсними й А и В.

Таким чином, пропозиція виду А/\В природно вважати дійсним у тому й тільки в тому випадку, коли дійсні обоє пропозиції А и В. Відповідне визначення запишемо в зручній і широко застосовуваній у математичній логіці формі таблиці істинності:

 

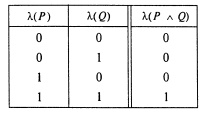
У перших двох стовпцях таблиці поміщені всілякі набори значень істинності висловлень А и В, а в третьому стовпці -відповідні значення істинності складеної пропозиції А/\В.

 

3. 2 Диз'юнкція

 

Логічне зв'язування «або» будемо позначати символом V. Пропозиція виду AVВ (А або В) умовимося вважати неправильним у тому й тільки в тому випадку, коли обоє пропозиції А и Б неправильні, тобто приймемо наступне визначення:

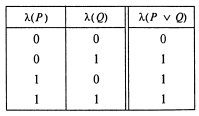
Це визначення закріплює за союзом «або» нерозділовий зміст, крім інших його тлумачень.

Відповідно до даного визначення пропозиція «Число 2- парне або число 2 -простої» є дійсним висловленням. Дійсними висловленнями також є пропозиції «Число 2- непарне або простої» і «Число 2 — парне або складене». Пропозиція «Число 2- непарне або складене», згідно із прийнятим визначенням, неправильно.

Очевидно, що всяка пропозиція, утворене з висловлень за допомогою певних у такий спосіб логічних зв'язувань «і» і «або», є висловленням, оскільки воно або істинно, або хибне.

Утвір складеного висловлення за допомогою логічного зв'язування називають логічною операцією. Операція, відповідна до союзу «і», називається кон’юнкцією ( від латинського conjunctio-«з'єднання»); союзу «або» відповідає операція, називана диз'юнкцією (disjunctio — «поділ»).

Помітимо, що в арифметиці операція і її результат мають різні назви — «додавання» і «сума», «множення» і «добуток»; логічні операції і їх результати (складові пропозиції) називаються однаково.

Визначення кон’юнкції й диз'юнкції природно узагальнюються для будь-якого числа складових висловлень:

Кон’юнкція n висловлень ( тобто пропозиція виду A1 /\A2 /\A3… /\An) дійсна тоді й тільки тоді, коли всі складові її висловлення дійсні;

диз'юнкція n висловлень (A1\/A2\/...\/An) неправильна тоді й тільки тоді, коли всі складові її висловлення неправильні.

Легко бачити, що якщо хоча б одне зі складових пропозицій —форма висловлювання, а всі інші висловлення, то складена пропозиція —форма висловлювання.

 

3 Заперечення.

 

Логічна операція, відповідна до логічного зв'язування «не» («невірно, що»), називається запереченням. Заперечення пропозиції А записується так: А. На відміну від кон’юнкції й диз'юнкції операція заперечення проводиться над одним висловленням і визначається таблицею із двох рядків:

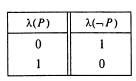
Із цього визначення випливає, що пропозиція і його заперечення не можуть бути ні одночасно дійсні, ні одночасно неправильні.

Приклади.

1. «3 рівно 2» (Л); «3 не рівно 2» (Л).

2. «У всякий трикутник можна вписати окруж ность» (Л); «Невірно, що у всякий трикутник можна вписати окружність» (Л).

У прикладі 1 заперечення неправильного висловлення є дійсним висловленням, у прикладі 2 заперечення дійсного висловлення є неправильним высказываниемт.

Якщо А — высказывательная форма, то А — також высказывательная форма. При тих самих наборах значень змінних высказывательные форми А и А стають висловленнями із протилежними значеннями істинності.

Пропозиція, що не містить формальних ознак заперечення (слів «не» або «невірно, що»), але, що має той же зміст, що й заперечення пропозиції А, будемо також уважати запереченням А. Наприклад, для пропозиції «Трикутник ABC — прямокутний» запереченням служить кожне з наступних пропозицій: «Треуголь- никнув ABC — не прямокутний»; «Невірно, що трикутник ABC — прямокутний»; «Трикутник ABC — косокутний».

 

4 Імплікація 

 

Логічна, операція, відповідна до союзу «якщо... те...», називається імплікацією. Будемо позначати цю операцію символом (. Запис А(У читається так: «якщо А, те В», або «А імпліцирує В».

Зрівняємо такі пропозиції: «Якщо число n ділиться на 4, то воно ділиться на 2»; «Якщо Іванов захоплений математикою, те Петров нічим, крім хокею, не цікавиться». Очевидно, що зміст союзу «якщо... те...» у цих пропозиціях не той самий. Визначення імплікації, представлене таблицею

 

 

відповідає змісту союзу «якщо... те...» у першій пропозиції. Насправді, визнаючи справедливість твердження «Якщо число n ділиться на 4, то воно ділиться на 2» для будь-якого натурального n, ми зобов'язано вважати дійсними такі висловлення, як «Якщо 16 ділиться на 4, те 16 ділиться на 2», «Якщо 18 ділиться на 4 те 18 ділиться на 2» і «Якщо 17 ділиться на 4, те 17 ділиться на 2», що відповідає першої, третьої й четвертої рядкам таблиці. Неправильного висловлення, відповідного до другого рядка таблиці, у силу справедливості вихідного твердження ми не одержимо ні при якім значенні n.

В імплікації АУ перший член А називається антецедентом ( від латинського antecedent — «попередній»), а другий член В — консеквентом [consequent — « наступний»).

З визначення імплікації випливає, що:

1) імплікація з неправильним антецедентом завжди дійсна;

2) імплікація з дійсним консеквентом завжди дійсна;

3) імплікація неправильна тоді й тільки тоді, коли її антецедент — дійсний, а консеквент — неправильний.

Прийняте визначення імплікації відповідає вживанню союзу «якщо.„те...» не тільки в математику, але в повсякденній, повсякденній мові. Так, наприклад, обіцянка приятеля «Якщо буде гарна погода, то я прийду до тебе в гості» ви розціните як неправду в тому й тільки в тому випадку, коли погода буде гарна, а приятель до вас не прийде.

Разом з тим визначення імплікації змушує вважати дійсними висловленнями такі пропозиції, як «Якщо 2-2=4, те Москва — столиця Росії» або «Якщо 2-2=5, то існує сніжна людина». Ці пропозиції, імовірно, видадуться безглуздими. Справа в тому, що ми звикли з'єднувати союзом «якщо... те» (також як і іншими союзами) пропозиції, зв'язані за змістом.

Але визначеннями логічних операцій зміст складових висловлень ніяк не враховується; вони розглядаються як об'єкти, що володіють єдиною властивістю — бути дійсними або неправильними.

 

5 Еквіваленція

 

Логічна операція, відповідна до союзу «тог- та й годі тоді, коли», називається еквіваленція.

Уведемо для позначення еквіваленції символ↔, Запис А ↔ В читається як «А тоді й тільки тоді, коли В».

Коли ми говоримо «А тоді й тільки тоді, коли В», те маємо на увазі, що обоє пропозиції А а В одночасно дійсні, або одночасно неправильні. Наприклад, говорячи «Я поїду в Київ тоді й тільки тоді, коли ти поїдеш у Львів», ми затверджуємо, що або відбудеться й те, і інше, або не відбудеться ні того, ні іншого. Відповідно до звичайного розуміння союзу «тоді й тільки тоді, коли» приймемо визначення:

 

 

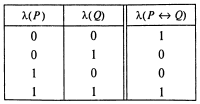
Таким чином, висловлення виду А↔ В істинно, якщо значення істинності висловлень А и В збігаються, і неправильно у протилежному випадку.

 

 

Вправи

1. Установите, які нз наступних пропозицій є висловленнями;  формами висловлювання:

а)3+2 = 5;

б) 3<2;

в) Зх<2;

г) х²>0;

д) «Число слів у цій пропозиції рівно симі»;

е) «Осінь — краща пора року»;

ж) « чи знаєте ви українську річ?»;

з) «У чотирикутнику протилежні сторони конгруентні»;

н) «У всякому чотирикутнику протилежні сторони конгруентні:»;

к) « У деяких чотирикутниках протилежні сторони конгруентні»;

л) «Існує число х таке, що х²<0»;

м) « Для всякого числа х \х\>0»;

и) «У місті N більш 100 000 жителів»;

о) «Існує найбільше натуральне число»;

2.          Укажіть, які з висловлень в упр. 1 дійсні н які — неправильні.
3.          У кожну  форму висловлювання з упр.1 підставте значення змінної так, щоб вийшло: Дійсне висловлення; неправильне висловлення.
4.          Кожну  форму висловлювання з упр. 1 перетворите в дійсне висловлення за допомогою слова «усякий:» або «існує».
5.          Придумайте по два приклади: а)    дійсного   висловлення; б)хибного висловлення; в) форми висловлювання із числовими змінними; г) форми висловлювання з нечисловими змінними; д) пропозиції, що не є ні висловленням, ні формою висловлювання.
6.        Визначите значення істинності наступних висловлень: а) «Париж розташований на Сене й 2+3 = 5»; б) «1 — просте число й 2- просте число»; в) «1 — просте число або 2 — просте число»; г) <Число 2 — парне або це число — простої»;
7.        Визначите значення істинності висловлень А, В, С и D якщо: а) А  (2-2 = 4) дійсне висловлення; б) В  (2-2 = 4) — неправильне висловлення; в) CV(2-2 — 5) — дійсне висловлення; г) D V (2-2=5) - хибне висловлення.
8.        Кожне з наступних пропозицій заміните кон’юнкцією або диз'юнкцією, що має той же зміст:

а) «Усі однозначні прості числа, більші двох, непарні»;

 б) «Кожний доданок суми а+6+із парне»;

в) « Принаймні одне з натуральних чисел я, n-1, n+1 парне»;

г) «Число а належить хоча б одному із множин А и В»;

д) «Існує натуральне число, більше 118 і менше 123, яке ділиться на 7»; е)«Квадратне рівняння має не більш двох корінь».

9.        Сформулюйте заперечення наступних висловлень; укажіть значення істинності даних висловлень і їх заперечень: а) «Місяць — супутник Марса»; б) «32 не ділиться на 4»; в) 5>2; г) 35; д) «Усі прості числа непарні».

 

Контрольні запитання:

1. Дайте визначення поняттю висловлювання?
2. Які ознаки висловлювання?
3. Дайте визначення функції істинності
4. Перелічить основні операції над висловлюваннями та зазначте випадки істинності цих операцій.