Лекція "Сортування масивів"

 

 

 

 

 

 

 

 

 

 

 

 

 

Обчислювальні алгоритми сортування

 

 

 

 

 

 

 

 

 

Вислови про сортування

Якщо слово, яке тобі потрібно відшукати, починається з (a), то дивись у початок книги, а якщо з (v), то в кінець. Знову якщо слово починається з (ca), то дивись у початок букви (c), а якщо з (cu), то в кінець. І так до кінця слова.

Інструкція зі словника англійської мови, 1604 р.

"Навіть якщо б сортування була майже марна, знайшлася б маса причин зайнятися нею! Винахідливі методи сортування говорять про те, що вона і сама по собі цікава як об'єкт дослідження."

/ Д. Кнут /

"Складається враження, що можна побудувати цілий курс програмування, вибираючи приклади тільки із завдань сортування."

/ Н. Вірт /

 

Мета:

• ознайомити студентів з методами сортування масивів, алгоритмами сортування, аналізом їх швидкодії і кількості використаних операцій порівняння та обміну;
• розвивати логічне мислення студентів, професійні компетентності фахівця у сфері ІТ-технологій;
• володіти  основами конструювання програмного забезпечення;
• використовувати інформаційні технології для рішення експериментальних і практичних завдань у галузі професійної діяльності;
• розвивати здатність вирішувати стандартні завдання професійної діяльності на основі інформаційної культури із застосуванням інформаційних технологій;
• здатність мати навички самостійної роботи на комп’ютері з використанням універсальних пакетів прикладних програм.

 

Навчально-методичне забезпечення, ТЗН: мультимедійних проектор EPSON-MG-850 HD, презентаційний матеріал,  роздатковий матеріал, конспект лекцій.

 

Вид заняття: лекція-візуалізація.

 

Література:

 

1. Коротєєва Т.О., Алгоритми та структури даних: навч. посібник / Т.Щ. Коротєєва.- Львів : Видавництво Львівської політехніки, 2014. - 280с.
2. Михальов О.І., Крамаренко В.В., Ялова К.М., Новікова К.Ю. Навч. посібник. - Дніпродзержинськ: ДДТУ. 2010. - 286 c.
3. Гнучких Л.А., Литвиненко Є.М., Мерлак О.В. Моделі та структури даних. Частина І Структури даних: Навчально-методичний посібник.-Х.:ХДТУБА, 2006.-78с.

 

Структура заняття

І Вступ. Організаційна частина

ІІ Актуалізація опорних знань

Повторення вивченого матеріалу шляхом фронтального опитування.

1. Що таке масив?
2. Види масивів.
3. Що таке сортування?
4. Якою є мета сортування?

 

 

 

 

ІІІ Виклад лекційного матеріалу

Повідомлення теми заняття, мотивація навчальної діяльності

 

План

1. Загальна характеристика сортування.
2. Сортування обміном.
3. Сортування вибором.
4. Сортування вставкою.

 

1. Загальна характеристика сортування.

Сортування - впорядковування набору однотипних даних по зростанню або спаданню. Мета сортування - полегшити подальший пошук елементів у такому відсортованому масиві.

Відмінною особливістю сортування є та обставина, що ефективність алгоритмів, що реалізують її, прямо пропорційна складності розуміння цього алгоритму. Іншими словами, чим легше для розуміння метод сортування масиву, тим нижче його ефективність.

Сортування є одним з найбільш зрозумілою категорією алгоритмів, оскільки процес сортування дуже добре визначений. Алгоритми сортування були піддані великому аналізу, і спосіб їх роботи добре зрозумілий. При необхідності відсортувати дані багато програмістів просто викликають стандартну функцію qsort(), що входить в стандартну бібліотеку C. Проте різні підходи до сортування мають різні характеристики. Попри те, що деякі способи сортування можуть бути в середньому краще, ніж інші, жоден алгоритм не є ідеальним для усіх випадків. Тому широкий набір алгоритмів сортування — корисне додавання в інструментарій будь-якого програміста.

Основна умова: метод сортування масивів повинен економно використовувати доступну пам'ять.

Існує багато різних алгоритмів сортування. Усі вони мають свої позитивні сторони, але загальні критерії оцінки алгоритму сортування такі:

• Наскільки швидко цей алгоритм сортує інформацію в середньому?
• Наскільки швидко він працює в кращому і гіршому випадках?
• Природно або неприродно він поводиться?
• Чи переставляє він елементи з однаковими ключами?^[

Швидкість сортування визначається кількістю порівнянь і кількістю обмінів.

Поведінка алгоритму сортування називається природним, якщо час сортування мінімальний для вже впорядкованого списку елементів, збільшується у міру зростання міри невпорядкованості списку і максимально, коли елементи списку розташовані в зворотному порядку. Об'єм роботи алгоритму оцінюється кількістю здійснюваних порівнянь і обмінів.

Найпростіші і очевидні методи називаються прямими і вимагають n² порівнянь. Програми цих методів легкі для розуміння і короткі (самі програми також займають пам'ять). Недоліком прямих методів є велика кількість порівнянь і перестановок.

Ускладнені методи вимагають невеликого числа операцій, але ці операції зазвичай самі складніші, і тому для невеликих масивів прямі методи виявляються краще, хоча для великих масивів їх застосовувати, звичайно, не слід.

Існує три загальні методи сортування:

• cортування за допомогою включення (by insersion);
• cортування за допомогою вибору (by selection);
• cортування за допомогою обмінів (by exchange).

2. Сортування обміном.

Сортування обміном (або бульбашкова сортування) - це найпростіший спосіб упорядкувати масив чисел, з точки зору витрат програмних ресурсів. Алгоритм бульбашкового сортування дуже простий для розуміння і легкий у реалізації.

До сортування обміном відносяться сортування бульбашкою та сортування (алгоритм) Шелла, Шейкерне сортування.

Алгоритм методу：

1. Ввести масив.
2. Порівняти два сусідні елементи, згідно заданої умови, виділити і при необхідності перемістити необхідний елемент (за І-ий прохід; визначити перший елемент).
3. Перейти до наступного проходу, не враховуючи вже визначеного елементу згідно п.2.
4. Виконати п.3 поки не залишиться остання пара елементів a_k i a_k-1 до повного сортування масиву.

При аналізі будь-якого алгоритму сортування корисно знати, скільки операцій порівняння і обміну буде виконано в кращому, середньому і гіршому випадках.

Алгоритм бульбашкового сортування виконує (n²-n)/2 порівнянь, де n — кількість сортованих елементів. Ця формула виведена на тій основі, що зовнішній цикл виконується n - 1 раз, а внутрішній виконується в середньому n/2 раз.

Алгоритм порядку n² не ефективний при великій кількості елементів, оскільки час виконання росте.

Приклад 1.

Застосуємо алгоритм сортування бульбашкою, щоб впорядкувати за зростанням такий масив:

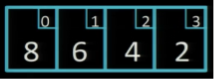
Прохід 1

Здійснюємо три обміни (червоним виділено елементи, що порівнюються):

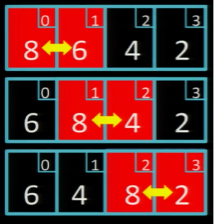
Прохід 2

Оскільки на проході 1 ми здійснили обмін, то робимо ще один прохід (тут також здійснюємо три обміни):

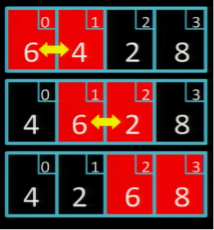
Прохід 3

Лише один обмін:

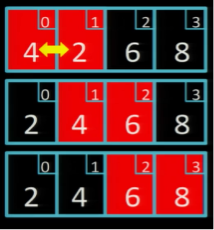
Хоча після цього проходу масив вже впорядковано, але оскільки був зроблений обмін, необхідно зробити ще один прохід.

Прохід 4

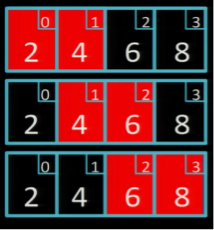
Це останній прохід, бо масив вже впорядковано і ми не зробили жодного обміну значень.

Псевдокод

Ініціалізувати лічильник

повторювати

  Встановити лічильник на 0

 

  Пройти в циклі весь масив

    якщо n-те значення більше за n+1-ше

      обміняти їх місцями

      збільшити лічильник 

поки (лічильник > 0)

 

3. Сортування вибором.

Сортування вибором (метод мінімальних елементів)- це найпростіший але найдовший метод. В основу цього методу покладено вибір відповідного елемента для певної позиції в масиві.

До сортування обміном відносяться турнірне сортування, пірамідальне сортування та сортування деревом.

Алгоритм методу：

1. Ввести кількість елементів n, їх значення.
2. Знайти в послідовності елемент за заданою умовою (min, max) – внутрішній цикл.
3. Поміняти його і перший елемент місцями .
4. Виконати п.2,3 з наступними елементами поступово, не  включаючи вже поміняні елементи доки не залишиться один останній елемент, тобто до повного сортування масиву.

На жаль, як і у бульбашковому сортуванні, зовнішній цикл виконується n - 1 раз, а внутрішній — в середньому n/2 раз. Сортування за допомогою вибору вимагає  (n²-n)/2 порівнянь.

Приклад

Впорядкуємо за зростанням масив, зображений нижче.

На початку роботи алгоритму, всі значення є невпорядкованими.

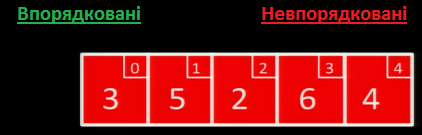
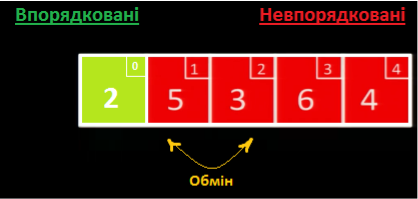
Шукаємо у масиві найменше невпорядковане значення. Це - 2, тому ми міняємо його місцями із першим невпорядкованим значенням 3:

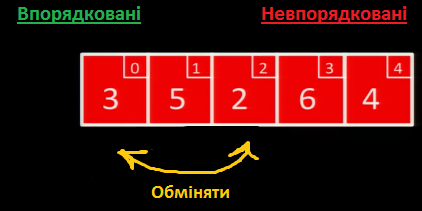
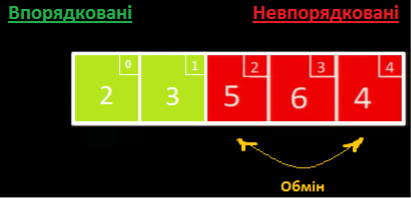
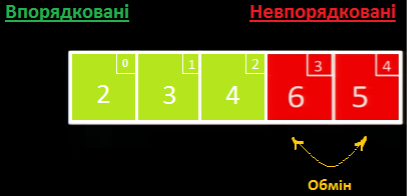
Далі ми обробляємо лише невідсортовану частину:

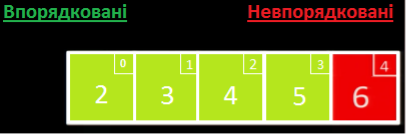
Отже, масив упорядковано.

Псевдокод

Для i в межах від 0 до n-1

  min = i

  для j в межах від i+1 до n-1

    якщо array[j] < array[min]

      min = j

    якщо min != i

      обмін array[min] та array[j]

 

4. Сортування включенням.

Сортування включенням — простий алгоритм сортування на основі порівнянь. Застосовують до частково впорядкованих масивів.

Алгоритм методу вставок

1. Ввести масив.
2. Перевірити масив  згідно заданої умови
3. Знайти  елемент А, що не відповідає умові
4. Знайти нове положення для елемента А, перевіривши послідовність спочатку згідно умови
5. Звільнити місце для елемента А_ВСТ, для чого зсунути частину послідовності  на одну позицію вправо
6. Вставити елемент А  на нове місце
7. Повторювати п.2–6 до повного впорядкування

На відміну від бульбашкового сортування і сортування за допомогою вибору, кількість порівнянь в сортуванні вставками залежить від первинної впорядкованості списку. Якщо список вже відсортований, кількість порівнянь рівна n - 1; інакше його продуктивність є величиною порядку n².

У сортування вставками є дві переваги.

По-перше, її поведінка природна. Іншими словами, вона працює менше всього, коли масив вже впорядкований, і найбільше, коли масив відсортований в зворотному порядку. Тому сортування вставками — ідеальний алгоритм для майже впорядкованих списків.

Друга перевага полягає в тому, що цей алгоритм не міняє порядок однакових ключів. Це означає, що якщо список відсортований по двох ключах, то після сортування вставками він залишиться впорядкованим по обох.

Попри те, що кількість порівнянь при певних наборах даних може бути досить низькою, при кожній вставці елементу на своє місце масив необхідно зрушувати. Внаслідок цього кількість переміщень може бути значною

Приклад

Як і в алгоритмі сортування вибором, спершу всі елементи масиву є невпорядкованими.

На першій ітерації алгоритму, ми беремо перше значення із масиву, і вставляємо його у список впорядкованих значень

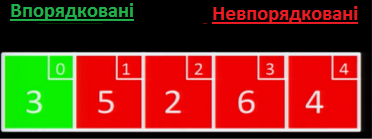
Далі, на другій ітерації алгоритму, ми беремо перше значення у невідсортованій частині масиву, і починаємо шукати для нього підходяще місце у вже відсортованій частині масиву. Оскільки 5 > 3, то ми вставляємо нове значення праворуч від старого.

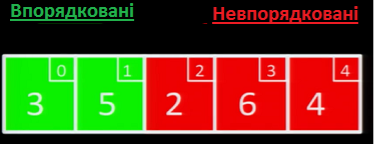
На наступній ітерації, ми беремо значення 2. Оскільки 2 < 5 та 2 < 3, необхідно вставити 2 ліворуч 3 та 5. Щоб зробити це, ми посуваємо трійку та п'ятірку праворуч, і вставляємо двійку на її місце:

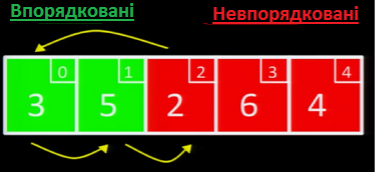
Оскільки наступний елемент, 6, - найбільше значення у відсортованій частині масиву, вставляємо її праворуч від 5.

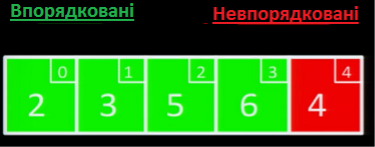
Останній елемент, 4, - менший за 5 та 6, але більший за 3 - тому ми вставляємо його між 3 та 5.

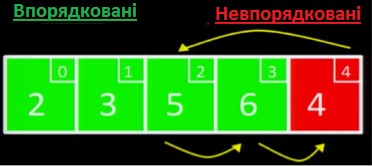
Масив відсортовано.

Псевдокод

Для і в межах від 0 до n - 1

  element = array[i]

  j = i

  поки ((j > 0) та array[j-1] > element)

    array[j] = array[j - 1]

    j = j - 1

  array[j] = element

 

IV Закріплення отриманих знань :

• Студенти коментують відеооролики з прикладами різних видів сортування.
• Демонстрація створення музики за допомогою алгоритмів сортування.
• Демонстрація створення картини за допомогою алгоритмів сортування.
• Фронтальне опитування:

1.          Що таке сортування?
2.          Алгоритм сортування вставками.
3.          Алгоритм сортування вибором.
4.          Алгоритм сортування обміном.

 

V Підведення підсумків заняття

 

IV Оголошення домашнього завдання:

• вивчити і закріпити знання лекції "Обчислювальні алгоритми сортування";
• підготуватися до практичної роботи на тему: "Основні алгоритми сортування";
• впорядкувати за зростанням масив методом вставки

а_і = 12, 20, 33, 14, 25, –2;

• впорядкувати за зростанням масив методом вибору

а_і = 22,20,33,14,25,16,14;

• впорядкувати за зростанням масив методом обміну

а_і = 5, 8, 10, 3, 9, 4.