Лінійне рівняння з однією змінною

Про матеріал

Розробка конспекту уроку алгебри 7 класу в темі "Лінійна функція". Допоможе вчителю яксно та швидко підготуватися до уроку

Перегляд файлу

Урок №6.

ЛІНІЙНЕ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ

Мета: повторити, поглибити та розширити знання учнів про види рівнянь з однією змінною, що зводяться до лінійних рівнянь з однією змінною (рівняння з модулем та рівняння, що містять дроби) та способи рівносильних перетворень таких рівнянь.

Тип уроку: поглиблення знань, засвоєння вмінь.

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання

ІІІ. Актуалізація опорних знань

Під час математичного диктанту повторюємо теоретичний матеріал та способи дій, розглянуті на попередньому уроці.

Математичний диктант

1. Придумайте і запишіть будь-яке лінійне рівняння з одним невідомим [].

2. Як називається рівняння []?

3. За яких умов рівняння [] має єдиний корінь (не має коренів)? Запишіть цей корінь.

4. Розв’яжіть рівняння [].

5. Розв’яжіть рівняння [].

6. Розв’яжіть рівняння [].

По завершенні роботи відповіді перевіряються, корегуються і повторюються означення лінійного рівняння з однією змінною та схема розв’язання лінійних рівнянь.

IV. Систематизація, поглиблення та розширення знань

1. Робота з випереджальним завданням

Розгляньте рівняння:

; ; .

За відомим алгоритмом виконайте порівняння (додаток 2).

Висновки: 1) Усі наведені рівняння можна записати у вигляді одного рівняння , де — будь-яке число.

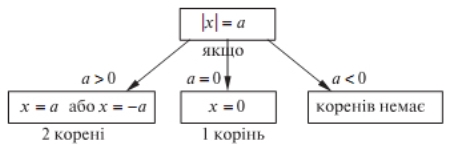
2) Спосіб розв’язування і кількість коренів цього рівняння залежить від знака числа , а саме:

2. Розширення знань

Як було вже сказано на попередньому уроці, розв’язання багатьох рівнянь, що мають одну змінну, зводиться до розв’язування лінійних рівнянь з однією змінною. Серед таких рівнянь можна виділити:

а) рівняння з модулем;

б) рівняння, що містять дроби.

Далі розбираємо розв’язування рівнянь названих видів.

а) .

Перш ніж починати пояснення, слід активізувати мислення учнів, запропонувавши порівняти рівняння з рівнянням виду .

• Чим відрізняється дане рівняння від рівняння ?

• Чим схожі ці рівняння?

• Чим схожий спосіб розв’язування (перший крок) і чим буде відрізнятися розв’язування?

Після цього робимо записи в зошитах (проводимо усні зауваження)

. (Спрощуємо вираз під знаком модуля.)

1) або 2) . (Оскільки , , , то або . Розв’язуємо лінійні рівняння.)

, .

Відповідь. 3; 0.

б) .

Перш ніж розв’язувати рівняння, слід порівняти його з іншими рівняннями, що були розв’язані раніше. Провести бесіду, розглянувши такі питання:

• Чим відрізняється дане рівняння від рівняння № 1 в домашньому завданні?

• Що спільного?

• Яку властивість рівносильних рівнянь можна використати, щоб позбутися дробів?

• Яка властивість дробів використовується при цьому?

Після цього можна записати розв’язання, додавши усні коментарі.

. (Знайдемо НСК (18; 12; 9) = 36 та помножимо на нього обидві частини рівняння.)

. (Виконаємо множення.)

;. (Виконаємо рівносильні перетворення, зведемо рівняння до лінійного і розв’яжемо його.)

, .

Відповідь. 6.

Висновки. Розібравши приклади а) та б) ми впевнилися в тому, що деякі рівняння з модулем, так само як і деякі рівняння з дробами (не всі!!!), шляхом виконання рівносильних перетворень та використання властивостей чисел можуть бути зведені до лінійних рівнянь з однією змінною.

V. Засвоєння вмінь

Виконання письмових вправ

№ 1. Розв’яжіть рівняння, що містять змінну під знаком модуля:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) .

VI. Підсумки уроку. Рефлексія

Ігровий момент «Знайдіть помилку»

Учень 7 класу Петрик Тяпляпкін сказав, що дуже добре навчився розв’язувати рівняння, що зводяться до лінійних, і показав, як він розв’язує рівняння. Ось його розв’язання.

а) ,